Purpose

Fast Field-Cycling MRI¹ (FFC-MRI) is a novel MRI technique in which the external magnetic field is switched during the imaging experiment. By doing this, FFC-MRI grants access to information which is invisible to conventional MRI scanners, including the variation of T₁ with magnetic field. These measurements, known as T₁-dispersion, exhibit great promise as a new form of endogenous image contrast, and may have application in the early diagnosis of a range of diseases including osteoarthritis², cancer and neurodegeneration. In our system, the use of a resistive magnet to perform field-cycling means that the B₀ field is subject to a slow drift with a corresponding drift in frequency. Even when this drift is controlled using an NMR lock or a current feedback loop, small off-resonant effects persist. This results in small discontinuities in k-space, which manifest as ghosting in the phase-encode direction. Here we present a post-processing technique³ which is able to correct these ghosts and recover the original image with no prior knowledge of the field-drift.

Methods

The magnet (Tesla Engineering Ltd, Storrington, UK) is of a resistive design and is driven by 18 current amplifiers (IECO, Helsinki, Finland). The main magnetic field is set and controlled by a 16-bit, high-precision DAC which provides a field resolution of 3 μT. This limits real-time field corrections to 3 μT, or approximately 125 Hz, which is sufficient to prevent severe off-resonance effects but still results in ghosting artefacts. We therefore developed a post-processing algorithm using MATLAB 2014a (Mathworks, Natick MA USA) to attempt to correct the phase errors. The algorithm takes the form of an iterative method inspired from similar techniques for correcting motion artefacts^4,5. As a minimisation criterion we used the image background; an image with no ghosting should have minimal background signal. During each iteration the algorithm estimates the phase correction for every line of k-space using a sequential programming (SQP) method, the image is reconstructed and the background signal is estimated. The algorithm terminates once the background signal has converged. Constraints were added on the SQP search in order to null the 1st order moment of the phase correction to prevent translation along the phase-encode direction. The algorithm was tested in simulations and on image data collected on phantoms and in vivo. For the simulations we used the Monte-Carlo method: a 128x128 artefact-free gradient-echo image was used as the base for 1000 test images with randomly added noise, phase scatter and amount of background area.

Results

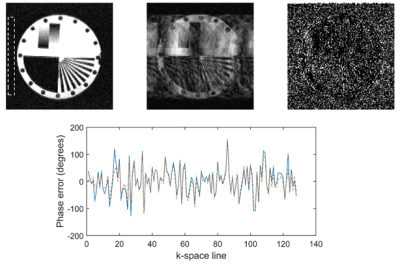
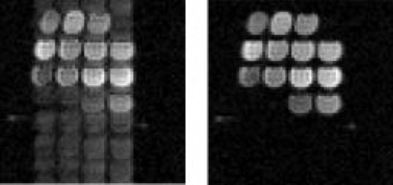
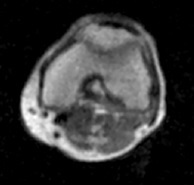
For the Monte-Carlo simulations none of the images failed to converge. Figure 1(a) shows the reference image while (b) shows the same image following the addition of random phase errors, and (c) shows the difference between the original and the corrected image. Figure 1(d) shows the agreement between the phase correction recovered by the algorithm and the ground truth error applied to the original image. The average reconstruction time for a 128x128 image was 7 s on a desktop i5 processor. The processing time follows a square relationship with the matrix size; upscaling the image to 512x512 increased the processing time to 104 s. Superior time efficiency can be realised by parallelising the corrections for multi-dimensional data. Experimental data from phantom (Figure 2) and in vivo (Figure 3) imaging reconstructed using the algorithm demonstrate excellent results with no visible ghosting.

Discussion

The algorithm presented here has demonstrated that artefact free images can be obtained on our FFC-MRI scanner even where there is a drift in resonant frequency without excessive post-processing time. So far we have only tested the algorithm on Cartesian sampled data, however the algorithm should be applicable to other sampling strategies. We have tested the algorithm only to correct the phase errors resulting from the frequency drift of our magnet, but it would be interesting to investigate applications for other types of artefact such as motion.

Acknowledgements

We acknowledge support for this project from the European Union, under Horizon-2020 project 668119, “IDentIFY”