Introduction

TRansmit Array Spatial Encoding (TRASE) is a relatively new MRI method^1,2 for which spatial encoding is achieved through the application of phase gradients of the B₁ field – rather than magnitude gradients of the B₀ field – and in general requires as many as two distinct phase-gradient coils per encoding direction. Moreover, traversal through k-space with TRASE requires a train of π-pulses generated by alternating phase-gradient coils. As a result, there is very strong motivation here to employ linear rather than rotating B₁ fields (lest the already large number of rf coils should further double) and to understand the full details of rapid π-pulse generation with such fields. This is particularly important for our ongoing evaluation^3,4,5 of the benefits and limitations of TRASE at low field, where the magnitude of the linear B₁ field may not be negligibly small compared to B₀ leading to a breakdown of the rotating wave approximation (RWA). Here we explore the unconventional trajectories on the Bloch sphere arising from the breakdown of the RWA. Our work reveals a complex interplay of Bloch-Siegert shift,⁶ B₁ start or end phase,⁷ and B₁ amplitude transients⁸ that must be taken into account to achieve the expected trajectory terminus.

Methods

We studied the effects and consequences of the breakdown of the RWA through analytical and numerical solutions of the Bloch equations. For convenience, we express the magnitude of the B₁ field as the parameter N_π = B₁/B₀, which is the number of cycles of the oscillating field required to achieve a π-radian rotation. As such, the continuous wave Bloch-Siegert shift⁶ becomes ΔB_cw = B₀/(4 N_π)². For all simulations presented here, we fixed the B₁ frequency to its nominal value ω₀, applied rectangular pulses of linear field B₁cos(ω₀ t + φ) along the x-axis in the laboratory frame, and managed any de-tunings through a field shift δB away from B₀. Experimental studies were performed in B₀ fields of a few mT or less, using both water and hyperpolarized ³He gas samples.

Results

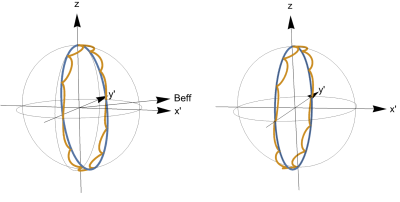
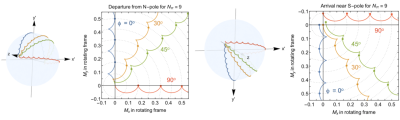
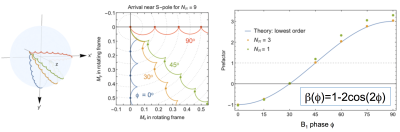
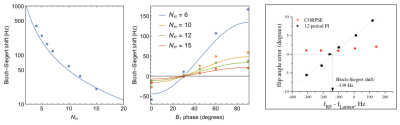
Numerical simulations are shown in Figures 1 through 4; experimental results are in Figure 5. Figure 1 highlights the general effects of the breakdown of the RWA due to a strong counter-rotating B₁ field: the trajectory undergoes cycloid motion and a perfect π-pulse cannot be achieved without de-tuning the field. Every half-period, the trajectory without/with de-tuning lands on that due to a rotating B₁ field with/without de-tuning of the same magnitude. Figure 2 highlights the fact that the specific details of the cycloid trajectory, and in particular its terminus, depends strongly on the phase of the B₁ field. Starting and stopping pulses at the cusps in the trajectory (ie. zero field and zero coil current, occurring every half-period) is an important strategy for eliminating further complications due to B₁ amplitude transients in real coils. As shown in Figure 3, a perfect π-pulse can always be achieved by de-tuning the field by δB = β ΔB_cw, where to lowest order the prefactor β depends only on the phase φ. In Figure 4, we show the effect of the breakdown of the RWA on a π-pulse intended to rotate transverse magnetization about the x’-axis in the rotating frame. Again, the appropriate de-tuning of the static field will achieve the desired rotation. In Figure 5, we present a small compilation of experimental results achieved to date. In particular, we show data that confirms the 1/ N_π² behavior of the Bloch-Siegert shift, as well as the magnitude and change of sign of the prefactor β(φ). The Bloch-Siegert shift is determined experimentally as the de-tuning δB required to achieve a perfect π-pulse. We also present a comparison of the performance a composite π-pulse versus a simple rectangular π-pulse. Arbitrary pulse shapes and durations have also been investigated.

Discussion and conclusion

We have made extensive numerical and experimental studies of the breakdown of the RWA due to a strong counter-rotating B₁ field. Our results show a rich behavior involving the Bloch-Siegert shift, B₁ start and stop phase, and B₁ amplitude transient that is of fundamental interest in magnetic resonance. It is of great practical importance for low-field MR applications, in particular TRASE MRI where one is more or less restricted to using large amplitude, linear B₁ fields. Achieving the expected trajectory terminus in this regime requires an appropriate phase-dependent de-tuning of the field. Using pulse durations and sequence timings that are half-integer multiples of the B₁ period is also beneficial.