2695
A Simple Method for Improved Correction of EPI Odd-Even Line Inconsistency1UIH America, Inc., Houston, TX, United States, 2United Imaging Healthcare, Shanghai, China
Synopsis
We have developed a simple method for EPI Nyquist ghosting artifacts removal. Our technique borrows the idea of GRAPPA, and extracts a non-biased kernel from imperfect multichannel EPI data to correct the odd-even line inconsistency. We have demonstrated both in-vivo and in-vitro that this strategy can significantly reduce Nyquist ghosts. The proposed method is quite simple and can be conveniently used with many current EPI correction techniques to generate ghosting-free images.
Introduction
Echo-Planar Imaging (EPI) is one of the fastest MRI sequences. It is widely used in applications requiring a high temporal resolution, such as functional MRI. It is also the standard approach for diffusion MRI sequences, which would otherwise be prohibitively long. However, there are some inherent inconsistencies between odd and even k-space lines, due to such as gradient delays and different eddy currents induced by readout gradients with opposing polarities. Such inconsistency results in the notorious Nyquist ghosts in EPI images1. The most widely used EPI ghost removal method requires the acquisition of non-phase-encoded lines, and subsequently estimates and corrects the odd-even line inconsistency including a phase and a delay along the readout direction1,2. However, because the correction is often imperfect and this model does not include more complicated k-space misalignment, such as shifts along the phase encoding direction, some level of ghosting often remains after the correction. We have developed a simple method for improved EPI data correction, which borrows the idea from GRAPPA3 and can be applied on multichannel EPI data. Our method is capable of correcting the k-space misalignment in two dimensions, and can effectively remove the Nyquist ghosts in addition to the conventional EPI correction.Theory
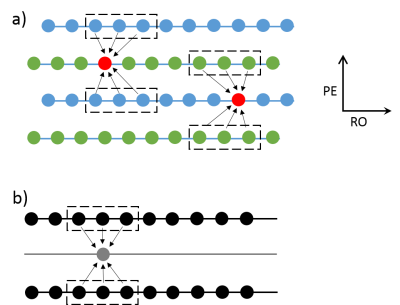
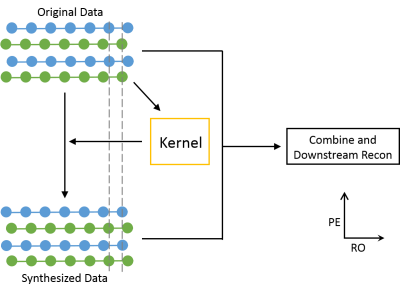
The proposed method is illustrated in Fig. 1. Although only k-space delay along the readout direction is shown in Fig. 1a, correction of other odd-even line inconsistencies can be understood similarly. Consider two kernels with support regions including only odd/even lines and targets containing only even/odd line data. It is straightforward to see that for the odd-fit-even case, the kernel will be biased such that it generates data shifted to the left. On the other hand, the kernel will be biased in the opposite direction for the even-fit-odd case. We set up the kernel-fitting least square problem including both patterns. The aforementioned biases will cancel out and a perfect kernel can be extracted (Fig. 1b). This kernel is then applied on the original data to generate a synthesized k-space data set (Fig. 2). Since the kernel is not biased, the even lines (green) of the synthesized k-space data, generated from the odd lines (blue) of the original k-space data, is shifted to the right, like the original odd lines. Similarly, the odd lines (blue) of the synthesized k-space data is shifted to the left, like the original even lines. It is important to note that the odd-even line inconsistency is opposite between the original data and synthesized data. Ghost-free images can be generated by complex summation of images produced by the two data sets, similarly to the PLACE technique proposed by Xiang et. al.4 Our proposed method can be used in complement to the traditional EPI correction method1,2 to remove residual Nyquist ghosts.Methods
Both phantom and volunteer head images were acquired. The phantom data were acquired on a uMR 560 1.5 T scanner (United Imaging Healthcare, Shanghai, China) with a 16 channel head coil. A gradient-echo EPI sequence was used for this study. Three echoes with phase encoding turned off were inserted after the excitation to collect information for traditional odd-even line correction1,2. 2D images were acquired with: slice thickness = 3.5 mm, FOV = 225×225 mm, resolution = 112×112, FA = 90°, TE = 53 ms, BW = 2250 Hz/pixel. The volunteer data were acquired on a uMR 770 3.0T scanner (United Imaging Healthcare, Shanghai, China) using a 24 channel head coil with a similar sequence.
All data were first corrected using the conventional method, with information extracted from the three echoes without phase encoding. The data were then reconstructed using either direct Fourier transform, or processed using the proposed method and then Fourier transform. Data from different channels were combined using sum of squares.
Results
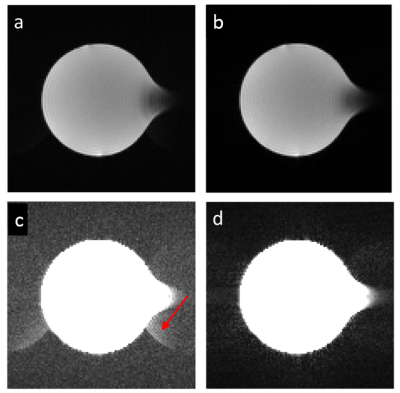
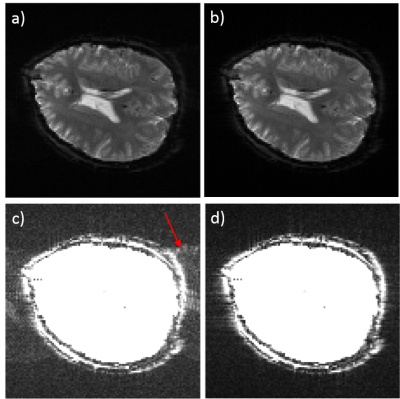
Fig. 3a-d compare water phantom images reconstructed with the traditional method and the proposed method. Fig. 3c-d were set to a smaller display scale to visualize the ghosts. Fig. 4a-d show brain images reconstructed using both approaches, with adjusted brightness for Fig. 4c-d. For both in-vitro and in-vivo cases, a significant reduction of Nyquist ghosts was observed.Conclusion
We have developed a simple method for EPI Nyquist ghosting artifacts removal. Our technique borrows the idea of GRAPPA, and can be applied on multichannel EPI data. We have demonstrated both in-vitro and in-vivo that this technique can significantly reduce Nyquist ghosts. The proposed method is simple and can be conveniently used in combination with the traditional 1D EPI correction method, as well as many other EPI correction procedures to generate ghosting-free images.Acknowledgements
No acknowledgement found.References
- Bruder H, Fischer H, Reinfelder HE, Schmitt F, Image reconstruction for echo planar imaging with nonequidistant k-space sampling. Magn Reson Med. 1992;23:311–323.
- Zhang W, Wu H, Jiang X, An image reconstruction method for the Echo-Planar Imaging sequence. CN Patent 104035059 A.
- Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A, Generalized autocalibrating partially parallel acquisitions (GRAPPA), Magn Reson Med. 2002 Jun;47(6):1202-10.
- Xiang QS, Ye FQ, Correction for geometric distortion and N/2 ghosting in EPI by phase labeling for additional coordinate encoding (PLACE), Magn Reson Med. 2007 Apr;57(4):731-41.
Figures