2690
kT-spokes: combining kT-points with spokes to ease ramp pulse design for TOF slab selection with parallel transmission at 7T1CEA/DRF/Joliot/NeuroSpin/UNIRS, Gif-sur-Yvette, France, 2Siemens Healthineers France, Saint-Denis, France, 3Laboratoire des Signaux et Systèmes, Université Paris-Saclay/CentraleSupélec/CNRS, Gif-sur-Yvette, France
Synopsis
TONE pulses counteract blood saturation through the imaged slab in TOF sequences, but their ramp profile is hampered by RF inhomogeneities at Ultra High Field. On the other hand, kz-spokes are known to compensate for in-plane B1+ heterogeneities in slice or slab selection. However, their design doesn’t address thru-slab heterogeneities. To address them, a new pulse type called “kT-spokes” is introduced. As TONE pulses, kT-spokes efficacy is demonstrated with pTx at 7T in comparison with mere equivalent kz-spokes.
INTRODUCTION
MR angiography Time-Of-Flight (TOF) sequences are sensitive to blood saturation (BS) effects as blood traverses the imaged slab in the human head, preventing the visualization of the whole arterial network. One efficient way to compensate for this saturation has been the use of ramp or TONE RF pulses, with thru-slab ascending flip angle (FA) profiles1,2. However, at 7T, in large-slab selection, B1+ heterogeneities hamper fidelity to the specified FA pattern. Previously, we addressed this issue by combining parallel transmission (pTx) and double-spoke ramp excitations3, thus fully embracing 7T SNR and contrast benefits4. The study demonstrated the efficiency of a spoke waveform design addressing the full three-dimensional problem as opposed to the traditional spokes that only mitigate the FA in-plane variations. Yet because of the large number of unknowns (waveform complex data-points for each spoke and every channel), optimization of tailored “3D-spokes” takes a long time (~30min), not quite compatible with clinical routine. The present work introduces a simpler spoke type, called “kT-spoke”, whose design takes only a few seconds while still considering the slab 3D B1+ distribution.MATERIALS & METHODS
The conventional spoke method optimizes the (kx, ky)-locations of consecutive selective excitations in the transmit k-space5. In the context of a mere uniform slab excitation, kT-spokes additionally allow the placement of the spoke centers in different (but nearby) kz-locations, thereby relaxing the degree of freedom needed for thru-slab homogenization. This method is equivalent to a kT-points pulse design6 where the target ROI is limited to the slab of interest, and where square subpulses are eventually replaced by kz-spokes, i.e. sinc-like waveforms played along with their selection gradient. Thus the only difference between spokes and kT-spokes is the presence of z-gradient blips in between RF subpulses. In the context of TONE pulses, for both conventional spokes and kT-spokes, the FA ramp profile was obtained by replacing the sinus-cardinal waveform by the inverse Fourier transform of the desired FA ramp. More precisely, the Fourier transform of an apodized sinc with TBW= 10 was multiplied by the latter before transforming it back.
Only triplets of spokes are considered in this study. The pulse design was formulated as a SAR- and power-constrained Magnitude Least Squares problem7 that jointly optimized the magnitude, phase, and placement in transmit k-space of each spoke on every transmit channel8, in the small tip angle approximation. Yet full Bloch equation simulations were run in the end to predict the slab FA maps and compute errors with respect to the desired ramp profile.
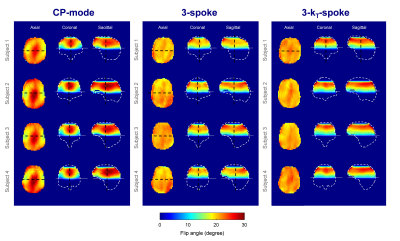
Experiments were performed on 5 volunteers (who signed an IRB-approved informed consent) using a MAGNETOM 7T scanner (Siemens Healthcare, Germany) and an 8-Tx/Rx head array (RAPID Biomedical, Germany). B0 and B1-maps of all subject brains were acquired with 5-mm resolution (B1-maps obtained from the XFL sequence9). Prior to the study, the kT-spoke performance was evaluated on a spherical water phantom with the AFI sequence10 to corroborate the FA Bloch simulations (Figure 1).
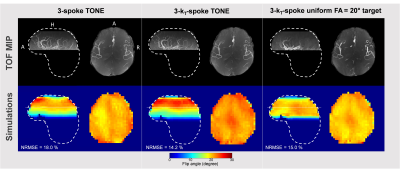
A FA-ramp from 10° to 30° was targeted with three bipolar spokes of 1 ms each. First, a comparison between conventional spoke and kT-spoke performances was carried out from simulation of the FA maps. Then, for either spoke strategy and only for the 5th subject, the computed composite pulse was integrated into a pTx TOF sequence with the following parameters: TR= 20ms, TE= 4ms, resolution= 0.4x0.4x0.5mm, FOV= 200x200x60mm, GRAPPA= 2, 6/8 partition partial Fourier and TA= 6 min. To evaluate the angiograms, a Maximal Intensity Projection (MIP) was performed on the TOF native images.
RESULTS
Regarding the 3D FA maps from the numerical simulations, kT-spokes showed an improvement of the slab profile for all subjects compared to conventional spokes (Figure 2). The FA Root-Mean-Square Error with respect to the prescribed ramp and normalized to the slab-center FA (NRMSE) was improved by 15% in average with the kT-spoke method (Table 1). The MIP performed on the 5th volunteer showed a significant enhancement of the depiction of the distal arteries compared to the acquisition made with a flat FA= 20° justifying the benefit of a ramp excitation (Figure 3). According to the simulation, the fidelity of the ramp generated by the kT-spoke design ensured a more accurate control of the BS compensation compared to the 3-spoke excitation. Indeed the contrast was slightly better and some additional arteries was restored (Figure 3).CONCLUSION
The clinically-viable kT-spoke design succeeds in counteracting the B1+ heterogeneities along the z-axis, particularly in wide off-centered slabs as shown here. Moreover this study demonstrates the benefit of FA-ramped kT-spokes for BS compensation at 7T by enhancing distal arteries visualization.
Acknowledgements
No acknowledgement found.References
1. Atkinson D, Brant-Zawadzki M, Gillan G, Purdy D, Laub G. Improved MR angiography: magnetization transfer suppression with variable flip angle excitation and increased resolution. Radiology. 1994;190(3):890–4.
2. Priatna A, Paschal CB. Variable angle uniform signal excitation (VUSE) for three-dimensional time-of-flight MR angiography. Journal of Magnetic Resonance Imaging. 1995;5(4):421–7.
3. Saïb G, Gras V, Mauconduit F, Boulant N, Vignaud A, et al. Double-Spoke Slab–Selective Ramp Pulse Design for UHF TOF MR Angiography. ISMRM 25th Annual Meeting & Exhibition, Apr 2017, Honolulu, United States.
4. Von Morze C, Xu D, Purcell DD, Hess CP, Mukherjee P, Saloner D, et al. Intracranial time-of-flight MR angiography at 7T with comparison to 3T. Journal of Magnetic Resonance Imaging. 2007 Oct;26(4):900–4.
5. Setsompop K, Wald LL, Alagappan V, Gagoski B, Hebrank F, Fontius U, et al. Parallel RF transmission with eight channels at 3 Tesla. Magnetic Resonance in Medicine. 2006 Nov;56(5):1163–71.
6. Cloos MA, Boulant N, Luong M, Ferrand G, Giacomini E, Le Bihan D, et al., kT-points: Short three-dimensional tailored RF pulses for flip-angle homogenization over an extended volume. Magnetic Resonance in Medecine. 2012 Jan: 67: 72-80.
7. Hoyos-Idrobo A, Weiss P, Massire A, Amadon A, Boulant N, et al. On variant Strategies to solve the MLS Optimization Problem in Parallel Transmission Pulse Design and Under Strict SAR and Power constraints. IEEE Transactions on medical imaging, VOL. 33, NO. 3, MARCH 2014
8. Dupas L, Massire A, Amadon A, Vignaud A, Boulant N. Two-spoke placement optimization under explicit specific absorption rate and power constraints in parallel transmission at ultra-high field. Journal of Magnetic Resonance. 2015 59-67
9. Amadon A, Cloos MA, Boulant N, Hang M-F, Wiggins CJ, and Fautz H-P, Validation of a very fast B1-mapping sequence for parallel transmission on a human brain at 7T, p. 3358, ISMRM 2012, Melbourne.
10. Yarnykh VL. Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magnetic Resonance in Medicine. 2007 Jan;57(1):192–200.
Figures