2679
Phase corrected Hadamard acquisition compared with three-dimensional (3D) Fourier encoding for functional MRI1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States
Synopsis
Three-dimensional (3D) functional MRI (fMRI) can be superior in localization of activation signals compared to two-dimensional (2D) fMRI because higher spatial resolution can be acquired due to potentially higher signal-to-noise ratio (SNR) and thinner slices. However in 3D, physiological noise reduces SNR due to higher signal at the k-space center; thus the number of slices should be decreased to reduce physiological noise. With Fourier encoding, acquiring a small number of slices results in excessive Gibbs ringing. In this study, we propose Hadamard reconstruction for 3D fMRI acquisition to avoid the artifact caused from Fourier encoding and return higher SNR.
Introduction
Higher spatial resolution is important in functional MRI (fMRI) for better localization of activation signals. Three-dimensional (3D) acquisition provides potentially higher signal-to-noise ratio (SNR)1,2 and can acquire thinner slices. Higher SNR and thinner slices play an important role in higher spatial resolution, therefore, 3D acquisition can be beneficial in fMRI. However, physiological noise contribution has a greater effect in 3D acquisition because physiological noise scales with signal intensity, which is higher in 3D compared to 2D acquisition. The 3D signal (S3D) increases as the number of slices increases compared to 2D signal (S2D) (Eqn.1), but is tempered by the increased T1 saturation with shorter TR.$$ S_{3D}=S_{2D}\cdot N_{slc}\frac{\sqrt{\frac{1-E_{3}}{1+E_{3}}}}{\sqrt{\frac{1-E_{2}}{1+E_{2}}}}, \ \ \ where \ \ E_{2}=exp(-\frac{TR}{T_{1}}), \ \ E_{3}=exp(-\frac{TR}{N_{slc}\cdot T_{1}}) \ \ \ \ \cdot\cdot\cdot \ (1) $$
The noise in 3D (σ3D) is higher due to physiological contributions (Eqn.2, λ is a constant)1,2.
$$\sigma_{3D} = \sigma_{o}^{2}+(\lambda \cdot S_{3D})^{2}\ \ \ \ \cdot\cdot\cdot \ (2)$$
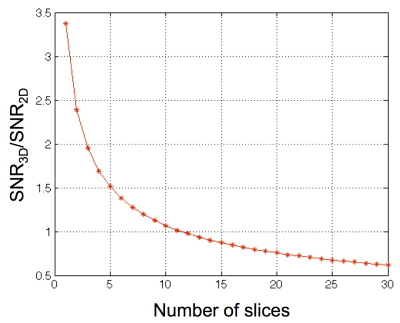
As shown in Fig.1, 3D has a benefit of SNR only when the number of slices is small. However, Fourier encoding, which is typically used in MRI, has large side lobes in the point spread function with small number of slices. In this study, we introduce Hadamard encoding3 with small number of slices (2 and 4) in 3D fMRI sequence to avoid artifact and benefit from increased SNR from simultaneous slice encoding. We developed a phase correction method to compensate for off-resonance across slices.
Methods
Data acquisition: We scanned a phantom using 2D with 20 timeframes and a 3D Fourier encoded spiral sequence with Hadamard 2 and 4 with 50 timeframes. Both data were acquired using a 3T GE whole-body MRI scanner equipped with a single-channel RF receive coil and a single-shot gradient-echo sequence with TE/TR=40/2700 ms, 1.7 mm x 1.7 mm x 3 mm voxels, FOV=22 cm×22 cm and 32 slices. Flip angles of 80, 70 and 45 degrees are used for 2D, 3D with Hadamard 2 and 3D with Hadamard 4, respectively. 2D data were used for phase correction in Hadamard reconstruction. We also scanned a human brain with IRB approval. Data were acquired using same scanner with same parameters except TE/TR=37/2500 ms.
Image reconstruction: Let Hn be a Hadamard matrix of order n (power of 2) and it contains ±1 in n × n matrix (Eqn.3).
$$H_{2}=\begin{bmatrix}1 & 1 \\1 & -1 \end{bmatrix},\ H_{4}=\begin{bmatrix}1 & 1 & 1 & 1 \\1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \end{bmatrix} \ \ \ \ \cdot\cdot\cdot \ (3)$$
Taking Hadamard 2 as an example (H2), with a sinc pulse for each slice S1 and S2 (Eqn.4) combined according to the Hadamard matrix for two acquisitions, $$S=\begin{bmatrix}S_{1} \\S_{2} \end{bmatrix} \ \ \ \ \cdot\cdot\cdot (4)$$ then the acquired data A can be written as A = H2S . Since Hadamard matrix has its own inverse, multiplying itself separates each slice (Eqn.5). $$ S = (H_{2})^{-1}A = H_{2}A \ \ \ \ \cdot\cdot\cdot (5) $$ We used Hadamard 2 and 4 matrix (H2 and H4) to acquire and reconstruct images. We found that off-resonance between slices can result in phase artifacts with Hadamard encoding. To resolve this artifact, we acquired 2D data with small number of timeframes (20 timeframes) as a correction factor applied to the acquired Hadamard data (Eqn.6).$$ Phase\ corrected\ image = Hadamard\ reconstructed\ data\times \frac{2D\ data\ with\ a\ few\ timeframes}{Hadamard\ reconstructed\ data} \ \ \ \ \cdot\cdot\cdot \ (6)$$ We compared reconstructed images and temporal SNR (tSNR) from 2D and 3D fMRI sequences with Hadamard.
Results
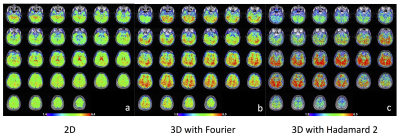
The reconstructed images using 2D and 3D fMRI sequence with Hadamard 2 and 4 are shown in Fig.2. For 3D Hadamard, reconstructed images with and without phase correction are also compared. 3D Hadamard reconstructed images successfully with phase correction. We also acquired brain data using 2D and 3D fMRI sequences with Fourier and Hadamard 2 as a preliminary work (Fig.3) and it showed that 3D with Hadamard has 115% higher tSNR compared to 2D.Discussion
We showed that the 3D sequence is beneficial for higher spatial resolution when the number of slices is kept small to reduce the physiological noise effect in 3D acquisition. In this study, we propose Hadamard reconstruction of small number of slices for 3D fMRI acquisition to avoid poor Fourier inversion properties with small number of slices. This method combined with a phase correction reconstructed images successfully compared to those from Fourier. From the preliminary brain data, the 3D sequence with Hadamard encoding showed substantially higher tSNR with higher spatial resolution. For future work, we will demonstrate task fMRI data and compare activation maps from Hadamard reconstruction to the one from 2D/3D with Fourier reconstruction.Acknowledgements
Funding for this work was provided by: NIH P41 015891.References
1. Physiological noise in oxygenation-sensitive magnetic resonance imaging. Kruger G, Glover GH, Magnetic Resonance in Medicine, 46(4): 631-637, 2001
2. Neuroimaging at 1.5 T and 3.0 T: comparison of oxygenation-sensitive magnetic resonance imaging. Kruger G, Kastrup A, Glover GH, Magnetic Resonance in Medicine, 45(4): 595-604, 2001
3. Hadamard matrices and their applications. Hedayat A., Wallis WD, Annals of Statistics. 6(6): 1184–1238, 1978
Figures