2677

A Data Driven Nyquist Ghost and Gradient Delay Correction for Navigator-Free 3D Planes on a Paddlewheel (POP) EPI
Daniel Stäb1, Tobias Wech2,3, and Markus Barth1

1The Centre for Advanced Imaging, The University of Queensland, Brisbane, Australia, 2Department of Diagnostic and Interventional Radiology, University Hospital Würzburg, Würzburg, Germany, 3Comprehensive Heart Failure Centre, University Hospital Würzburg, Würzburg, Germany

Synopsis

3D planes-on-a-paddlewheel (POP) echo-planar imaging (EPI) is an effective non-Cartesian readout scheme realized by rotating conventional EPI readout planes about the phase encoding axis. Navigator based phase correction schemes are typically employed to account for gradient timing errors, associated trajectory errors and artifacts. In this work, we propose to use “Self Consistency for an Iterative Trajectory Adjustment” SCITA for an improved and purely data-driven removal of trajectory misalignment artifacts. As the actual k-space trajectory is derived from the imaging data, navigator acquisitions can be omitted and echo, repetition and acquisition times may be considerably shortened.

Introduction

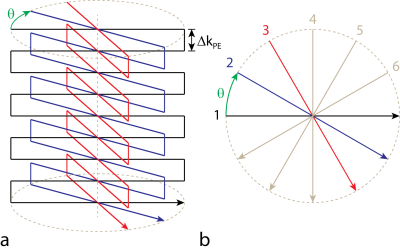
3D planes-on-a-paddlewheel (POP) echo-planar imaging (EPI) is a non-Cartesian readout scheme realized by rotating conventional EPI readout planes about the phase encoding axis (Fig. 1). The technique is effective for distortion minimization and was recently employed for whole-brain quantitative susceptibility mapping (QSM) at ultra-high field1.

Gradient timing errors are known to cause severe artifacts in EPI. Phase correction algorithms2, based on additional navigator echoes, typically have to be employed to remove the Nyquist ghosting, which arises from the shift of odd and even echoes with respect to each other along the phase encoding axis in k-space. In 3D POP EPI, an additional misalignment of the projections within the radial readout planes is introduced, which is typically neglected by navigator-based phase correction algorithms.

In this work, we propose to exploit “Self Consistency for an Iterative Trajectory Adjustment” (SCITA)3 for a purely data-driven removal of trajectory misalignment artifacts in 3D POP EPI. As the additional acquisition of navigator echoes can be omitted, the approach may facilitate shorter echo, repetition and acquisition times.

Methods

SCITA exploits the inherent oversampling of central k-space in radial imaging and obtains an estimate of the actual k-space trajectory that can be finally used for gridding. To that end, the trajectory correction technique iteratively maximizes the data consistency across the individual projections in the oversampled part of k-space by shifting individual projections with respect to the rest of the acquired k-space data by means of the GRAPPA operator4.

Measurements were performed on a non-commercial 7 T whole-body research MRI scanner (Siemens Healthcare, Erlangen, Germany) under institutional review board permission. The system was equipped with a Tx/32 channel Rx head array (Nova Medical, USA) and 3rd order shimming was employed for all measurements. One healthy 34-year-old volunteer was examined, after obtaining written informed consent and approval of the local ethics committee, and 3D POP EPI images were obtained at 1.5 mm isotropic spatial resolution using following acquisition parameters: FOV = 170 x 170 x 37 mm3, 172 projections with linearly increasing azimuthal angle within the interval [0;π[, TR = 36 ms, TE = 19 ms, ES = 1.03 ms, flip angle = 12°, ramp sampling = 6.4%. At the beginning of each readout train, 3 additional navigator echoes were acquired. All images were reconstructed offline using Matlab (The Mathworks, Natick, USA). The non-uniform fast Fourier transform (NUFFT) framework5 was used for gridding, followed by a Fourier transformation along the phase encoding axis and sum-of-squares coil combination.

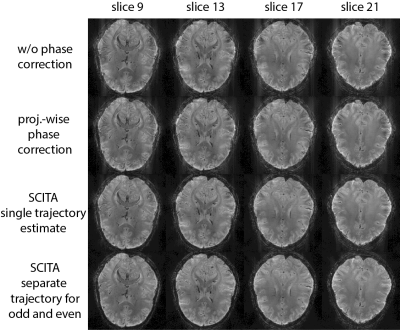
To test the performance of SCITA, images were reconstructed

  1. without any correction,
  2. using a navigator based phase correction2 for each projection before the gridding step,
  3. using a SCITA trajectory estimate obtained within the radial plane containing the echo (phase encoding step 13) for the reconstruction of all radial planes, and
  4. using a separate SCITA trajectory estimate for odd and even readout planes/phase encoding steps.

For the latter reconstruction, the trajectory estimates were obtained from the radial plane containing the echo and the adjacent radial plane (phase encoding step 12). To achieve a proper alignment of those two trajectories in the separate odd/even reconstruction, each trajectory was centered by iteratively maximizing the sum-of-squares k-space DC signal at k = 0 upon the application of multiple linear phase ramps in image space.

In all cases, SCITA was employed iteratively as described elsewhere3 with continuously decreasing shift lengths of 0.33, 0.15, 0.1, 0.07, 0.03 and 0.01 Δk with 20 iterations per shift length.

Results

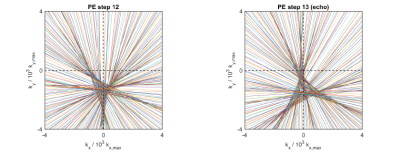
Obtained SCITA trajectory estimates reveal a clear misalignment of the individual projections in the center of k-space and distinct trajectory differences between odd and even echoes/phase encoding steps (Fig. 2). Images reconstructed without and with the navigator-based phase correction show typical misalignment artifacts of radial trajectories, which become less apparent for the reconstruction with the single SCITA trajectory estimate and are mostly removed for the odd/even SCITA reconstruction, which incorporates different trajectory estimates for odd and even echoes (Fig 3).

Conclusion

SCITA can be successfully employed to mitigate trajectory misalignment effects in 3D POP EPI. The improved outcome is considered a direct consequence of taking into account all trajectory misalignment components perpendicular to the readout direction. As the trajectory correction is estimated directly from the imaging data, additional navigator acquisitions can be omitted and echo, repetition and acquisition times may be considerably shortened. In addition, the approach avoids artifacts arising from time dependent effects (e.g. eddy currents) that cause discrepancies between navigator and image acquisition.

Acknowledgements

No acknowledgement found.

References

  1. Stäb D, Bollmann S, Langkammer C, et al. Accelerated mapping of magnetic susceptibility using 3D planes-on-a-paddlewheel (POP) EPI at ultra-high field strength. NMR Biomed. 2017;30:e3620.
  2. Heid O. Method for the phase correction of nuclear magnetic resonance signals. United States Patent Application Publication US6043651 (2000).
  3. Wech T, Tran-Gia J, Bley TA, Köstler H. Using self-consistency for an iterative trajectory adjustment (SCITA). Magn. Reson. Med. 2015;73:1151–1157.
  4. Seiberlich N, Breuer FA, Blaimer M, Barkauskas K, Jakob PM, Griswold MA. Non-Cartesian data reconstruction using GRAPPA operator gridding (GROG). Magn Reson Med 2007;58:1257–1265.
  5. Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using min–max interpolation. IEEE Trans. Signal Process. 2003; 51: 560–574.

Figures

Fig 1: 3D POP EPI readout scheme. Conventional EPI readout planes are rotated about the phase encoding axis resulting in a paddlewheel shaped readout trajectory.

Fig 2: Trajectory estimates (central k-space) for the 12th and 13th phase encoding step. The trajectories of odd and even echoes differ considerably.

Fig 3: Images of 4 partitions (left to right) reconstructed from the 3D POP EPI data, without any correction (top row), navigator-based phase correction (2nd row) and SCITA based trajectory corrections (3rd and 4th row). The best result is achieved when trajectory differences between odd and even echoes are considered in addition to misalignment effects within the radial planes (4th row).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
2677