Synopsis

For banding-artifact reduction in cardiac cine bSSFP imaging, we present a highly accelerated frequency-modulated sequence that can be used to acquire three phase-cycles within a short breath-hold. A reconstruction that exploits redundancies between the phase-cycles enables the high acceleration. Acquiring more phase-cycles facilitates a flatter spectral profile after phase-cycle combination. We formulate a regularization term for the reconstruction that is general to any number of phase-cycles to consistently achieve good image quality in multiple subjects.

Introduction

Methods

The frequency modulation scheme in [1] is applied. For each cardiac phase, $$$N_{p}=3$$$ effective phase-cycles are acquired in interleaved heartbeats. A number of TRs, $$$n_{FM}$$$, with total duration less than the shortest expected RR interval is chosen based on the heart rate. The phase increment increases by $$$360^\circ/(N_pn_{FM})$$$ each TR for $$$n_{FM}$$$ repetitions to reach the next phase-cycle and then remains constant until the next trigger (Fig. 1a). For typical values, the modulation rate is less than a $$$0.7^\circ$$$ RF-phase-increment increase per TR and each effective phase-cycle contains less than a $$$6^\circ$$$ range in the phase increment. Therefore, we do not expect the frequency modulation to significantly alter the contrast or introduce artifacts. In all acquisitions, $$$30^\circ$$$ of partial dephasing in the slice-select direction is used to lessen near-band flow artifacts [5].

A segmented acquisition with uniform undersampling is used, but the k-space sampling pattern is shifted every cardiac phase; the sampling is also shifted between phase-cycles (Fig. 1b). Therefore, averaging the cardiac phases and phase-cycles generates fully sampled data for parallel-imaging calibration. The shifting sampling pattern in k-t space also causes undersampling artifacts to reduce wavelet sparsity (Fig. 1c), so we hypothesize that $$$\ell$$$1-wavelet regularization helps suppress undersampling artifacts even though the sampling is not pseudorandom.

Similar to in [2], the images are reconstructed using:

$$\underset{x}{\arg\min}\left\|SFC_Rx-y\right\|_2^2+\mu_p\left\|Px\right\|_1+\mu_w\left\|W x\right\|_1$$

where $$$x$$$ is the images, $$$C_R$$$ applies receiver sensitivity profiles, $$$F$$$ is a two-dimensional FFT in the spatial dimensions, $$$S$$$ is k-space sampling, $$$y$$$ is the acquired k-space data, $$$W$$$ is a three-dimensional spatial and temporal wavelet transform, and $$$\mu_p$$$ and $$$\mu_w$$$ control regularization strength. Here, we reformulate $$$P$$$, the transform that exploits redundancy between phase-cycles, to handle a general number of phase-cycles. We approximate the $$$i^\textrm{th}$$$ phase-cycle cine loop $$$x_i$$$ as $$$x_i=C_{Pi}m$$$ where $$$m$$$ is the cine loop with no banding and $$$C_{Pi }$$$ is a diagonal matrix that applies the $$$i^\textrm{th}$$$ phase-cycle`s banding profile. In other words, all the phase-cycles should be consistent with a single, underlying cine and calibrated phase-cycle profiles. If the profiles are normalized such that $$$\sum_j^{N_p}C_{Pj}^HC_{Pj}=I$$$, then, ideally,

$$C_{Pi}\sum_j^{N_p}C_{Pj}^H x_j=x_i$$

Accordingly,

$$Px\triangleq\begin{bmatrix}C_{P1}\sum_j^{N_p}C_{Pj}^Hx_j\\\vdots\\C_{PN_p}\sum_j^{N_p}C_{Pj}^Hx_j\end{bmatrix}-\begin{bmatrix}x_1\\\vdots\\x_{N_p}\end{bmatrix}\label{eq:PCcost2}$$

For estimation of $$$C_{Pi}$$$, a moving average of cardiac phases with length equal to the undersampling rate $$$R$$$ generates fully sampled data [6], which is reconstructed to form calibration images $$$\widetilde{x}$$$. An average over all time is not possible because the phase-cycling varies with cardiac phase. The $$$n^\textrm{th}$$$ diagonal entry of­ $$$C_{Pi}$$$ is

$$C_{Pi,n}=\frac{\widetilde{x}_{i,n}}{\sqrt{\sum_i\widetilde{x}_{i,n}^*\widetilde{x}_{i,n}}}$$

Four healthy volunteers were imaged at 1.5T using an eight-channel cardiac coil. Cine loops of axial slices were acquired using a multiple-acquisition standard-phase-cycled sequence (static phase-cycling) and the previously described frequency-modulated sequence (dynamic phase-cycling). The parameters were: 24-28 cm isotropic field-of-view, 192x162 matrix size, 1.4 ms TE, 3.3-3.4 ms TR, and 30 ms temporal resolution. The scans were 30 heartbeats for static phase-cycling and 28 for dynamic with $$$R=2$$$ undersampling and 12 heartbeats for static and 10 for dynamic with $$$R=6$$$. Static phase-cycling requires two additional heartbeats than dynamic for stabilization periods between the phase-cycles.

Results and Discussion

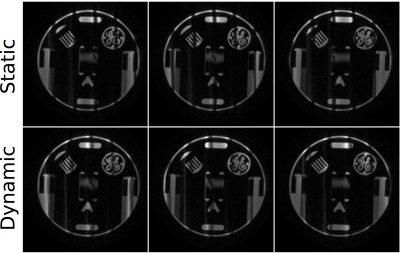
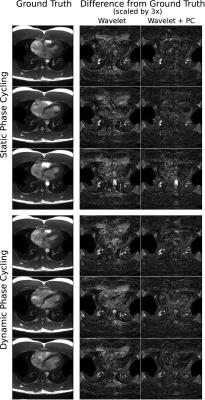
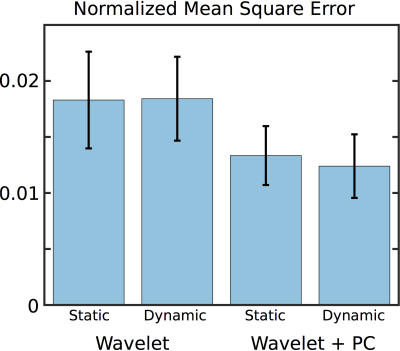
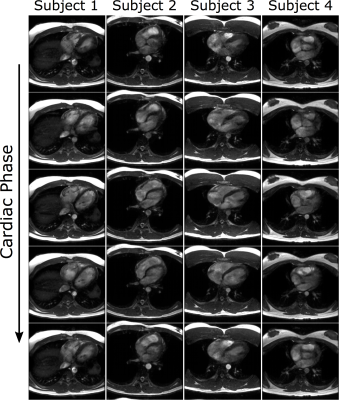
In a phantom (Fig. 2) as well as in all subjects (not shown), similar results were observed between static and dynamic phase-cycling, suggesting that the frequency modulation did not introduce artifacts. Fig. 3 shows the ground truth $$$R=2$$$ images (reconstructed using SENSE) of one subject and difference images for reconstructions after retrospective undersampling to $$$R=6$$$. The proposed regularization reduces the average mean-square error across all subjects by ~30% compared to wavelet regularization alone (Fig. 4). High-quality images are obtained from prospectively undersampled $$$R=6$$$ data in all four subjects even though the receive coil has only eight channels (Fig. 5).

Thus, we generalized acquisition and reconstruction strategies to acquire three phase-cycle bSSFP cardiac cine in only ten heartbeats, the same scan time as conventional two-fold-accelerated single-acquisition-bSSFP cine with matched parameters. This enabled good-quality banding-free bSSFP cine imaging within a short breath-hold.

Acknowledgements

References

[1] Datta A, Baron CA, Ingle RR, Cheng JY, Nishimura DG. Breath-held phase-cycled cardiac cine MRI using slow frequency modulation. Proc. 24th ISMRM, Singapore, May 2016. p. 3214.

[2] Baron C, Datta A, Nishimura D. Dynamically phase-cycled bSSFP cardiac cine in a single breathhold with phase-cycle consistency regularization. Proc. 25th ISMRM, Honolulu, May 2017. p. 5075.

[3] Markl M, Pelc NJ. On flow effects in balanced steady-state free precession imaging: Pictorial description, parameter dependence, and clinical implications. J Magn Reson 2004; 20:697–705.

[4] Storey P, Li W, Chen Q, Edelman RR. Flow artifacts in steady-state free precession cine imaging. Magn Reson Med 2004; 51:115–122.

[5] Datta A, Cheng JY, Hargreaves BA, Baron CA, Nishimura DG. Mitigation of nearband balanced steady-state free precession through-plane flow artifacts using partial dephasing. Magn Reson Med 2017 [Epub ahead of print]

[6] Kellman P, Epstein FH, McVeigh ER. Adaptive sensitivity encoding incorporating temporal filtering (TSENSE). Magn Reson Med 2001; 45:846–852.