2669

Improving image reconstruction with Phase Encoding Shifting of Successive IMaging slices (PESSIM)

José P. Marques¹, Daniel Gomez¹, and David G. Norris¹

¹Donders Centre for Cognitive Neuroimaging, Radboud University, Nijmegen, Netherlands

Synopsis

In this work we explore the added incoherence introduced when shifting the undersampling pattern in the phase enconding direction in successive slices, both when doing standard in-plane acceleration in 2D imaging or Simultaneous Multi-Slice (SMS) imaging with CAIPI trajectories. To be able to explore this incoherence, we treat both the 2D imaging and SMS imaging as one volumetric problem where the physically successive slices are forced to be coherent.

Introduction

Parallel imaging (PI) offers the possibility to reduce acquisition time thanks to the complementary information present in the various receiver channels¹. k-space trajectories such as those used in CAIPIRINHA² minimize PI reconstruction noise amplification by maximizing the spatial distance between aliased points. In compressed sensing³, the acceleration is facilitated by use of incoherent under-sampling schemes that generates aliasing that are penalized using a sparsifying transform.

Theory

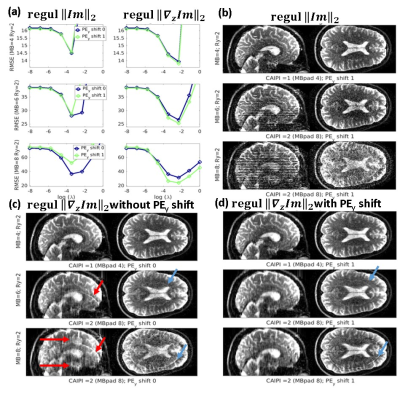
When reconstructing undersampled data, noise amplification and aliasing artifacts are directly related to the particular undersampling pattern ($$$ M_z $$$) used. Figure 1 shows the aliased reconstruction arising from inplane and SMS undersampling patterns in successive slices. It can be seen that a small shift in the $$$k_y$$$ direction increases significantly the gradient across aliased slices ($$$||\nabla _z \tt{Im}\\$$$). Thus, in this work we explore the formulation of the in plane reconstruction problem as:

$$ \min_{\tt{Im}} || y(k_x,k_y,z,c) - M_z \cdot \mathcal{F}\cdot C \cdot \tt{Im}|| ^2_2 + ||\lambda \mathcal{O} \tt{Im}||_{2/1}$$ [Eq. 1]

Where $$$ y $$$ was the measured data, $$$ \mathcal{F} $$$ represents a 2DFFT and $$$ C $$$ are the coil sensitivities calculated using ESPIRIT as implemented in the BART toolbox 4. $$$ O $$$ is a regularization operator that can be either the identity or the gradient across successive slices $$$ \nabla _z $$$ applied in either a l2 or l1 manner.

The SMS problem can be formulated as:

$$ \min_{\tt{Im}} || y(k_x,k_y,kz,z,c) - M_z \cdot \mathcal{F} \cdot \mathcal{R} \cdot C \cdot \tt{Im}|| ^2_2 + ||\lambda \mathcal{O} \tt{Im}||_{2}$$ [Eq. 2]

Where y(k_x,k_y,kz,z,c) represents the measured SMS data in the volumetric framework⁵, $$$ \mathcal{F} $$$ now represents a 3DFFT and $$$ \mathcal{R} $$$ is a reshaping operator that transforms the 3D space into a 4D dataset where the 3^rd dimension is the MB factor (eventually padded to accommodate integer blips)⁵ and the 4^th dimension is the number of SMS acquired.

Methods

Data of a healthy volunteer was acquired on a 3T (Siemens) using a 32-channel coil using a TSE protocol: TR/TE=4100/99msecs, res=0.5x0.5x1mm, MatrixSize=448x448x128, concatenations=8, total acquisition time=13mins. Coil sensitivity maps were derived from the centre 24 lines of k-space using BART reconstruction toolbox⁶.

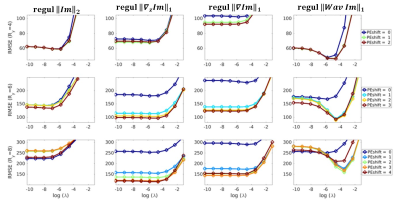
To evaluate the impact of the variation of undersampling pattern and regularization, the data was first decimated to correspond to a resolution of 2mm isotropic, the inplane acceleration ($$$ R_y$$$) was varied from 2-8 and the phase encoding increment in successive slices were varied from $$$0$$$ to $$$ 0.5R_y$$$.

Various regularization operators, $$$ \mathcal{O} $$$, were used: $$$||\tt{Im}|| _2$$$, TV across the slice direction($$$||\nabla _z \tt{Im}|| _1$$$), 3DTV ($$$||\nabla \tt{Im}|| _1$$$) and Wavelet in the slice direction ($$$||Wav\tt{Im}|| _1$$$). The reconstructed images were compared to the ground truth (reconstructed with no undersampling) in terms of RMSE.

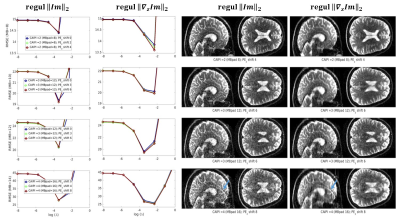
Similar analysis were performed for SMS acceleration (varied from 4 to 12, with CAIPI shifts of 1/4FOV), with $$$R_y=1$$$ and $$$ R_y=2$$$ and introducing either $$$ PE_z$$$ or $$$ PE_y$$$ shifts.

Results

Figure 2 shows the plots of RMSE of the reconstructed image vs the norm of the regularization enforced for different inplane accelerations. It shows that the reconstruction quality is independent of the k-space undersampling pattern used up to acceleration factors of 4, when the introduction of the PE shift gains an added value when using regularization operators that imposed coherent structure across slices.

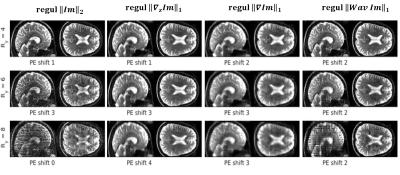
Figure 3 shows examples of reconstructions with the optimal parameters as found in Fig2. It can be seen that the improved reconstruction when using $$$||\nabla_z \tt{Im}||$$$ is obtained at a small cost of increased smoothness in the slice direction (which is significantly increased using $$$||\nabla \tt{Im}||$$$).

When extending the work to SMS imaging, and in the absence of in plane acceleration, the improvements of introducing the PE shift in the z-direction are minor (see Fig4 ) but become substantial when in-plane acceleration is introduced and the sampling of successive slices is shifted in y-direction as could be anticipated from Fig1.

Conclusions

PESSIM is a technique that could be easily implemented in most 2D and SMS techniques being used in MRI and we are optimistic that it can contribute to significantly accelerate imaging when inplane undersampling is used. Here we have used the assumption of smoothness along the phase encoding direction but other methods used in dynamic imaging might be equally valid.

Acknowledgements

This study is partly supported by the Advanced Brain Imaging with MRI (ABRIM) project, funded by EU-Marie Curie Actions and NWO.

References

1. Pruessmann, K. P., Weiger, M., Scheidegger, M. B. & Boesiger, P. SENSE: sensitivity encoding for fast MRI. Magn. Reson. Med. 42, 952–962 (1999).

2. Breuer, F. A. et al. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn. Reson. Med. 53, 684–691 (2005).

3. Lustig, M., Donoho, D. & Pauly, J. M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 58, 1182–1195 (2007).

4. Uecker, M. et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 71, 990–1001 (2014).

5. Zahneisen, B., Poser, B. A., Ernst, T. & Stenger, V. A. Three-dimensional Fourier Encoding of Simultaneously Excited Slices: Generalized Acquisition and Reconstruction Framework. Magn. Reson. Med. 71, 2071–2081 (2014).

6. Martin Uecker, Jon Tamir, Frank Ong, Christian Holme & Michael Lustig. BART: version 0.4.01. (Zenodo, 2017). doi:10.5281/zenodo.817472

7. Langkammer, C. et al. Quantitative susceptibility mapping: Report from the 2016 reconstruction challenge. Magn. Reson. Med. (2017). doi:10.1002/mrm.26830

Figures

Top and bottom panels show examples of inplane and SMS accelerations of 4. Columns relate to a shift of the sampling pattern by 0, 1 and 2 k-space positions. Top subpanels show corresponding the k-space undersampling mask. Bottom subpanels show the magnitude and phase aliased reconstructions of the undersampled data of two successive slices. The introduction of the PE shift, in the y and z direction (see yellow arrows in top and bottom panels respectively), only increased the through-slice gradient of the aliased reconstruction (see below phase images) in the first case.

Plots of the RMSE between reconstructed image and ground truth as a function of regularization value. First Second and third row correspond to acceleration factors of 4, 6 and 8. The different columns represent different regularization strategies: l2 norm, Total Variation along the z direction, Total Variation in the three spatial dimensions and Wavelet regularization (note that the three latter were reconstructed using a ADMN algorithm as implemented in BART toolbox). Different colors represent different PE shifts in the phase encoding direction. Y axis have been harmonized across acceleration factors.

Sagittal and transversal view of the optimal reconstructions (minimum RMSE to ground truth) for different in-plane accelerations (4, 6 and 8 in the 1st 2nd and 3rd row) using different regularization strategies: l2 norm, Total Variation along the z direction, Total Variation in the three spatial dimensions and Wavelet regularizatio. Wote that the 3D regularization introduces significantly more blurring in the reconstructed image, while the wavelet regularization functions well at lower accelerations (Fig.2) but it's flexibility retains slice to slice encoding artifacts introduced in the encoding.

Plots of the RMSE between reconstructed image and ground truth as a function of regularization value. Different rows correspond to different SMS factors from 8 to 14. In the 1st and 2nd column, l2 norm and gradient along the z direction regularization are shown. Different colors represent different PE shifts in the z phase encoding direction (See Figure 1). CAIPI blips and MBpad (should be interpreted as in Ref. 5) correspond to FOV shift ¼ . 3rd and 4th column show the optimum reconstructions for each regularization. Blue arrows highlight artifacts at MB 16.

(a) Plots of RMSE as a function of regularization value with: rows showing SMS factors from 4 to 6 combined with 2x inplane acceleration; columns showing l2 and gradient along the z regularizations. Different colors represent different PE shifts in the y direction. (b) and (d) show sagittal and transverse slices of the reconstruction that minimizes the RMSE to the ground truth using l2 norm and gradient along the z direction regularization respectively. (c) shows the optimum reconstructions when no in-plane PE shift is used. Blue arrows highlight common artifacts between images while red arrows highlight artifacts that disappear when in-plane PEshift is used.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

2669