2665

Enabling long excitation pulses in algebraic ZTE imaging by dead-time reduction via dual acquisition with alternative RF modulations
Romain Froidevaux1, Markus Weiger1, and Klaas Paul Pruessmann1

1ETH Zurich and University of Zurich, Zurich, Switzerland

Synopsis

MRI of tissues with short transverse relaxation times raises both scientific and clinical interest and can be performed with zero echo time MRI. However, as RF excitation is done under the radial encoding gradient, flip angle amplitudes and uniformity are limited. This issue can be circumvented by using longer modulated pulses. However, pulse length is limited by dead-time-induced central k-space gaps getting too large for robust image reconstruction. In this work, we propose a new approach that enables the use of long RF pulses in algebraic ZTE by utilizing their intrinsic encoding properties to fill part of the dead-time gap.

Introduction

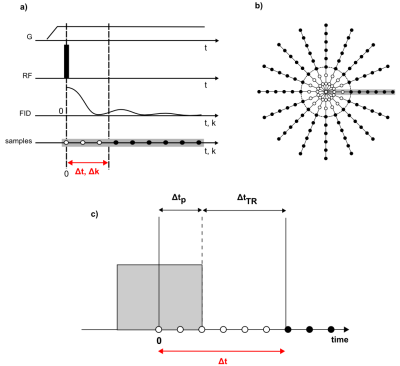
MRI of short-T2 tissues is of interest for clinical and scientific applications1 and can be efficiently performed with algebraic zero-echo-time (ZTE) imaging2 (Figure 1). However, as RF excitation is performed under the radial encoding gradient, with usually applied hard pulses and restricted B1, flip angle amplitudes and uniformity are limited. Therefore, Ernst angle may not be achieved and the creation of T1 contrast is hampered. This issue can be circumvented by using longer modulated pulses3. However, in this case, pulse length is limited by dead-time-induced central k-space gaps getting too large to enable robust image reconstruction4. To handle large gaps, techniques have been proposed to provide missing data by additional acquisitions at lower gradient strengths5,6 or to apply schemes with alternating excitation and reception7. However, they come at reduced SNR efficiency or partly increased susceptibility to artifacts from components with very short T28.

In this work, we propose a new approach referred to as P-ZTE (where P refers to pulse) that enables using long RF pulses in algebraic ZTE by utilizing their intrinsic encoding properties. The principle is demonstrated with 1D simulations and phantom imaging.

Theory

In standard algebraic ZTE reconstruction2, 1D projections are obtained from radially oversampled data by applying $$v = F\cdot s \qquad (1) $$ with voxel intensities v, sampled data s, and the reconstruction matrix F being the pseudo inverse of the encoding matrix given by $$E_{m,j} = exp(i2\pi\cdot k_{m}\cdot r_{j}) \qquad (2) $$ where m and j count k-space and spatial positions, respectively.

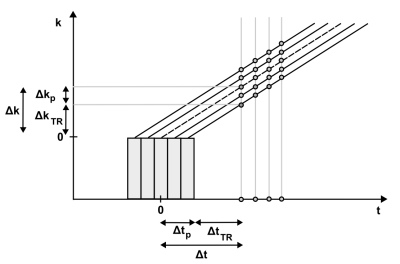
Here, we propose an expanded reconstruction method that takes into account the known complex-valued spatial profile of the RF pulse $$$p_{q}(r_j)$$$ to reduce the effective gap from $$$\Delta k $$$ to $$$\Delta k_{TR}$$$ (Figure 2).

Thus, the modified encoding matrix is $$ E_{(qm),j}=p_q(r_j)\cdot exp(i2\pi\cdot k_{m}\cdot r_{j}) \qquad (3) $$

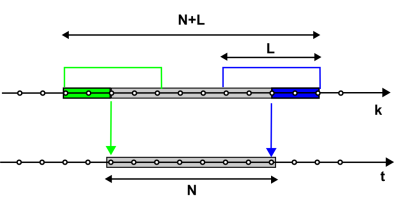
with q indexing different RF pulses. The above matrix is still ill-conditioned for standard ZTE data (q = 1) with large gap because the system to be solved for image reconstruction has more unknowns than equations (Figure 3). However, the conditioning can be strongly improved by adding a second ZTE acquisition performed with a different pulse profile (q = 2). E.g., a slight change in the carrier frequency of a frequency-swept pulse is sufficient to improve the conditioning to a degree that allows artifact-free image reconstruction. A frequency offset corresponds to shifting the pulse profile in the spatial domain, and for a pulse providing uniform excitation, the important contribution arises from the near-quadratic phase. The achieved improvement corresponds to reducing the effective gap $$$\Delta k_{eff} $$$ from $$$\Delta k $$$ to $$$\Delta k_{TR}$$$ (or the effective dead time $$$\Delta t_{eff} $$$ from $$$\Delta t $$$ to $$$\Delta t_{TR}$$$).

Methods

For 1D simulations, data was created by direct application of the encoding matrix (Eq. 3) to an oversampled simulated object. After adding noise to the data, images were reconstructed by applying Eq. 1.

Measurements were performed in a 3T Achieva MRI system (Philips Healthcare). Modulated pulse shapes were transmitted using a 1H-free birdcage coil9,10 through symmetrically biased T/R switches11 and NMR signal was acquired with a stand-alone spectrometer12. Pulse profiles were measured separately with a pickup coil directly connected to the spectrometer. Images were reconstructed using standard ZTE reconstruction2 with the adapted encoding matrix of (Eq. 3).

Results

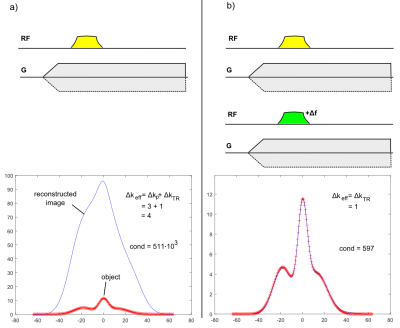
The 1D simulations in Figure 4 demonstrate the improvement of P-ZTE versus standard ZTE. As described previously4, ZTE imaging at large k-space gaps suffers from ill-conditioning, thus leading to considerable noise amplification appearing as low-frequency image distortions. By providing additional information by means of a second acquisition performed with a different RF pulse, the effective gap can be decreased from $$$\Delta k $$$ to $$$\Delta k_{TR}$$$, thus significantly improving the conditioning of the reconstruction and hence the image.

The potential of P-ZTE is illustrated on real data in Figure 5. Despite considerably reduced power, the SNR of the P-ZTE image is increased due to the long modulated RF pulse.

Discussion and Conclusions

A new approach was proposed for enabling long RF pulses in algebraic ZTE imaging, thus providing larger flip angles with uniform excitation. In contrast to standard ZTE, the effective gap size is independent from the pulse length and only determined by the time required for switching from transmit to receive operation. Despite doubling the acquisition time, SNR efficiency is hardly changed, as the second acquisition acts similar as normal averaging. Nevertheless, a detailed quantitative analysis is required to explore differences with respect to related techniques5-7.

Acknowledgements

No acknowledgement found.

References

1. Graeme M. Bydder, Gary D. Fullerton, Ian R. Young. MRI of Tissues with Short T2s or T2*s. Wiley; 2012.

2. Weiger M, Pruessmann KP. MRI with Zero Echo Time. eMagRes. 2012;1:311–322.

3. Schieban K, Weiger M, Hennel F, Boss A, Pruessmann KP. ZTE Imaging With Enhanced Flip Angle Using Modulated Excitation. Magnetic resonance in medicine. 2014;74:684–693.

4. Weiger M, Brunner DO, Tabbert M, Pavan M, Schmid T, Pruessmann KP. Exploring the bandwidth limits of ZTE imaging: Spatial response, out-of-band signals, and noise propagation. Magnetic resonance in medicine. 2015:74:1236–1247.

5. Grodzki DM, Jakob PM, Heismann B. Ultrashort echo time imaging using pointwise encoding time reduction with radial acquisition (PETRA). Magnetic Resonance in Medicine. 2012;67:510–518.

6. Wu Y, Dai G, Ackerman JL, Hrovat MI, Glimcher MJ, Snyder BD, Nazarian A, Chesler D a. Water- and fat-suppressed proton projection MRI (WASPI) of rat femur bone. Magnetic resonance in medicine. 2007;57:554–67.

7. Idiyatullin D, Corum C, Park J-Y, Garwood M. Fast and quiet MRI using a swept radiofrequency. Journal of magnetic resonance. 2006;181:342–9.

8. Froidevaux R, Weiger M, Brunner DO, Dietrich BE, Wilm BJ, Pruessmann KP. Filling the dead-time gap in zero echo time MRI: Principles compared. Magnetic Resonance in Medicine. 2017. DOI 10.1002/mrm.26875

9. Rösler MB, Weiger M, Brunner DO, Schmid T, Pruessmann KP. An RF birdcage coil designed for an insert gradient coil dedicated to short-T2 MRI. In Proceedings of the 26th Annual Meeting of ISMRM, Honolulu. 2017:2668.

10. Rösler MB, Weiger M, Schmid T, Brunner DO, Froidevaux R PK. Ultrasonic soldering on glass for the construction of MRI coils with minimized background signal in short-T2 images. In Proceedings of the 33rd Annual Scientific Meeting of ESMRMB, Vienna, Austria. 2016:87.

11. Brunner DO, Furrer L, Weiger M, Baumberger W, Schmid T, Reber J, Dietrich BE, Wilm BJ, Froidevaux R, Pruessmann KP. Symmetrically Biased T/R Switches for NMR and MRI with Microsecond Dead Time. Journal of Magnetic Resonance. 2016;263:147–155.

12. Dietrich BE, Brunner DO, Wilm BJ, BarmeT C, Gross S, Kasper L, Haeberlin M, Schmid T, Vannesjo SJ, Pruessmann KP. A field camera for MR sequence monitoring and system analysis. Magnetic Resonance in Medicine. 2016;75:1831–1840.

Figures

Figure 1: ZTE acquisition sequence. a) RF excitation is performed while the radial encoding gradient is already on. Signal acquisition is started immediately but data in and near the pulse cannot be acquired due to the dead-time. b) The sequence shown in a) is repeated with different gradient orientations in order to acquire 3D k-space in a radial fashion. c) Dead time contributions. The dead time ($$$ \Delta t $$$) is composed of half of the pulse duration ($$$ \Delta t_p $$$) and the time to switch from transmit to receive operation ($$$ \Delta t_{TR} $$$) .

Figure 2: P-ZTE principle, Part 1. The RF pulse can be considered a series of short block pulses, each creating a small portion of transverse magnetisation. The applied gradient dephases the created magnetisation as soon as it is created. Hence, each acquired sample is a sum of the previously created portions of magnetisation representing different k-space locations. In the P-ZTE reconstruction, the effective dead time gap is reduced from $$$\Delta k$$$ to $$$\Delta k_{TR}$$$ by utilizing the encoding properties of the RF pulse to recover data lost during the time $$$\Delta t_p$$$.

Figure 3: P-ZTE principle, Part 2: Time-domain data corresponds to a convolution of the pulse with the k-space representation of the object. This convolution mixes N+L unknown k-space values into N time points (with L the pulse duration in acquisition samples). The task of P-ZTE is to de-entangle k-space values by the inversion of a linear system of equations. With only one acquisition, this system is ill-conditioned because the number of unknown(N+L) is larger than the number of equations(N). However, a second acquisition with a different pulse brings N additional equations to the system allowing a reasonably well-conditioned inversion.

Figure 4: 1D simulations. a) In a standard ZTE acquisition, positive and negative k-space halves are acquired with 2 excitations performed with the same RF pulse and opposite gradient polarities. In this simulation, the effective gap ($$$\Delta k_{eff}$$$) is 4 and is composed of half the pulse duration(3) + the T/R-switching time(1), leading to a very ill-conditioned reconstruction. b) In P-ZTE, a second ZTE acquisition is performed with a different pulse (here an off-resonance equivalent to a 2-pixel shift is added). In doing so, the effective gap is decreased by the contribution of the pulse and the condition is strongly improved.

Figure 5: Imaging of an oil bottle at 3T (BW=100 kHz): Left: Standard ZTE imaging. A single acquisition was performed with a block pulse of 5 $$$\mu s$$$ and 500 W ($$$ \Delta k=\Delta k_p+\Delta k_{TR}=1$$$). Right: P-ZTE imaging. Two acquisitions were performed with sweep pulses of 100 $$$\mu s$$$ and 100 W with off-resonance of +-2kHz. Pulse profiles were measured with a loop coil and the image was reconstructed with the P-ZTE algorithm ($$$\Delta k=\Delta k_p+\Delta k_{TR}=5+1 = 6,\qquad \Delta k_{eff} = \Delta k_{TR} = 1$$$).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
2665