Synopsis

Inexpensive MRI scanners based on permanent magnets present a promising diagnostic tool for developing countries. For very inhomogeneous fields an ill-posed system of equations has to be solved in order to obtain an image. Due to the low signal-to-noise ratio, direct attempts at generating high resolution images yield poor results. In this research, super-resolution reconstruction is considered as an alternative. By first obtaining low resolution images and then applying super-resolution, high resolution images of better quality can be obtained.

Introduction

In countries such as Uganda, MRI is unaffordable at even major referral hospitals and medical schools. For such developing countries, conventional MRI devices are too expensive and too difficult to install, maintain and operate. MRI scanners based on Halbach arrays of permanent magnets may yield an inexpensive and sustainable alternative [Cooley, 2015]. One of the main drawbacks of such a scanner is the low signal-to-noise ratio (SNR). Therefore, we need advanced reconstruction algorithms to obtain high resolution images. This research focuses on whether super-resolution reconstruction can be used to improve the quality of the images to such an extent that brain diseases like hydrocephalus can be treated.

Image reconstruction

Super-resolution reconstruction

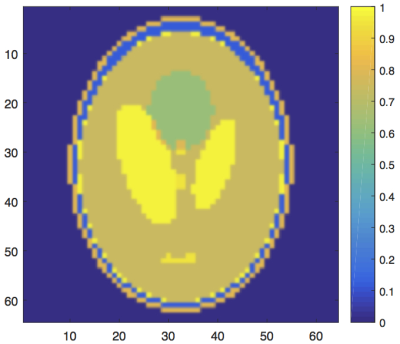
In order to obtain a sufficient amount of data to reconstruct an image, we simulate the measured signal based on 36 different rotations of our 2D phantom image (see Figure 1). Two different approaches are compared. The first is directly combining all measured signals into one high resolution (HR) image, the second consists of reconstructing 9 low resolution (LR) images (in each image, the phantom is rotated over a different angle) and using these to form an HR image. This is done by applying super-resolution reconstruction [Park, 2003]. Denoting the desired HR image by $$$\mathbf{x}$$$ and the set of LR images by $$$\{\mathbf{y}_k\}_{k=1}^N$$$, the model is described by $$\mathbf{y}_k = D_kB_kG_k\mathbf{x} + \mathbf{v}_k. \quad \quad \text{(3)}$$ Here, $$$\mathbf{v}_k$$$ is a noise vector and $$$D_k$$$, $$$B_k$$$ and $$$G_k$$$ are a downsampling, blurring and geometric deformation matrix, respectively. These three operators can be replaced by a single matrix $$$W_k := D_k B_k G_k$$$. Defining $$\mathbf{y} := \begin{pmatrix} \mathbf{y}_1 \\ \vdots \\ \mathbf{y}_k \end{pmatrix}, \quad W := \begin{pmatrix} W_1 \\ \vdots \\ W_k \end{pmatrix}, \quad \mathbf{v} := \begin{pmatrix} \mathbf{v}_1 \\ \vdots \\ \mathbf{v}_k \end{pmatrix} \quad \quad \quad \text{(4)}$$ yields one system of equations: $$\mathbf{y} = W\mathbf{x}+\mathbf{v}. \quad \quad \text{(5)}$$ Again, total variation regularisation is used to obtain a minimisation problem: $$\min\limits_{\mathbf{x}} ||\mathbf{y}-W\mathbf{x}||_2^2+μ||F\mathbf{x}||_1, \quad \quad \text{(6)}$$ where $$$μ$$$ is the regularisation parameter.

Results

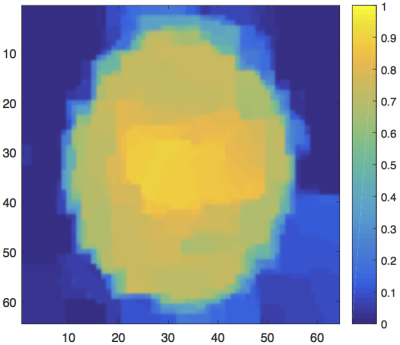
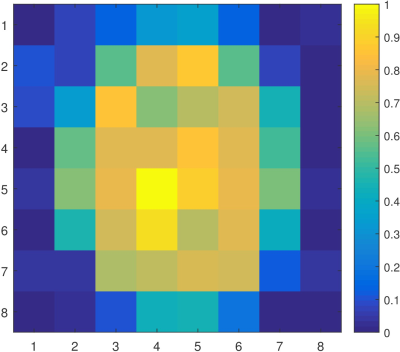
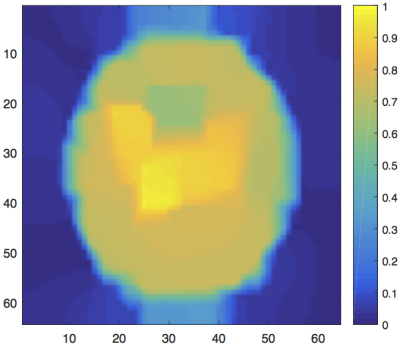
The SNR was set to 0.5. First, a direct approach was taken: the image was modelled as having 64x64 pixels. Then, solving minimisation problem (2) with the corresponding A yields the image shown in Figure 2. In order to use super-resolution, 9 LR images of 8x8 pixels were reconstructed. This was done by grouping the 36 signals into 9 groups of 4 signals. The solution was modelled as an 8x8 pixel image. Minimisation problem (2) was solved with the appropriate A for each of the groups. One of the 9 resulting LR images is shown in Figure 3. By applying super-resolution to these 9 images, the HR image in Figure 4 is obtained.

Discussion

Conclusion

Acknowledgements

References

Cooley C, et al. Two‐dimensional imaging in a lightweight portable MRI scanner without gradient coils. Magnetic resonance in medicine, 2015; 73 (2): 872-883.

Park S, et al. Super-resolution image reconstruction: a technical overview. IEEE signal processing magazine, 2003, 20 (3): 21-36.