Synopsis

A key challenge of MRI is development of an accurate model of noise generation which are integral to generation of high-resolution images. Currently, motion induced noise is addressed at algorithmic level. Here, we present a novel physical model which incorporates the role of mechanical vibration of body parts in generation of additional frequency components in the emitted radio frequency spectrum around the precession frequency. The mathematical model was validated through a computational simulation which led to the discovery that beats generated as a result of mechanical vibrations of the source lead to ghosting and blurring effects.

Introduction

Enhanced signal to noise ratio leads to high resolution of images in MRI [1]. Noise in MRI has been studied from the perspective of thermodynamic fluctuations on magnetization and its relaxation [2] which tend to influence precession and relaxation [3] along with spatial drift of nuclei [4]. Motion of the subject is also an additional source of noise which is addressed at algorithmic level [5] . However, the fundamental aspect of additional frequency components generated as a consequence of mechanical vibration of the sample remains unexplored. The objective of current work is development and validation of a novel model of generation of noise in MRI under the mechanical vibration of the source,which results in additional spectrum components around the precession frequency which blurs the final image.

Methods

In an MRI system, the magnetic moment oscillates with a precession frequency, ω₀=γB₀, where γ is the gyromagnetic ratio and B₀ is the applied magnetic flux density. The magnetic flux density B at a distance r from a source in a medium with permeability μ₀ having a magnetic moment m oscillating at a frequency ω is expressed as. B(r)=(µ₀)/(4π)(msinωt)/r^3.. If the initial position of the magnetic moment shows a periodic spatial shift at a frequency ω_m, at velocity defined by v=v=v_msinωt, the value of r can be found by integrating v with respect to time and it will have an impact on the generated magnetic field. The net change in magnetic flux density at a distance r can be expressed as follows,

B(r,t)=(µ0)/(4π)(v_msinω_mt,)(3mcosω₀t)/r^4. It can be simplified as, B(r,t)=(3µ₀)/(4πr⁴)mv_m[cos(ω_mt-ω₀t)-cos(ω_mt+ω₀t)] which implies beats formation. The additional frequencies generated has corresponding impact on the magnetization and the relaxation times T₁ and T₂ in the Z and XY plane respectively.

For Hydrogen ions at 1 T, the precession frequency is 42.574MHz [1]. During imaging, if the source is vibrating at a frequency of 1kHz, which corresponds to a period of 1 ms , an additional frequency band would be observed in the output image. This source vibration are caused by movement of different body parts like vocal tract, respiratory system,or unintended body part movement by the subject.

Simulation and Results

We developed a mathematical model while incorporating the effect of mechanical vibrations of the source on the magnetic moment in MRI systems. The decay of magnetization in the XY plane under beats formation can be expressed as, M_XY=M_XY0e^-t/T₂ [cos(ωmt-ω0t)-cos(ωmt+ω0t)], where M_XY0 is the initial value of magnetization in the XY plane. Similarly, the decay of magnetization in the Z plane is M_Z=M_Z0e-t/T₁ [cos(ω_mt-ω₀t)-cos(ω_mt+ω₀t)], where M_Z0 is the initial value of magnetization in the Z plane.

This model introduces the effect of source vibration on the MRI image reconstruction from the quantitative data (T₁ and T₂) collected from MRI machine of strength 1 Tesla and precession frequency of 42.576 MHz.

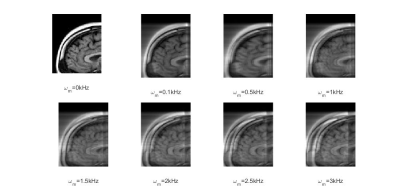
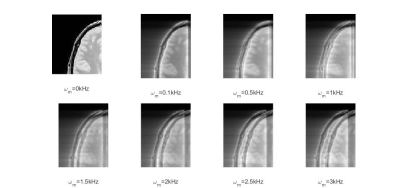
The effect of simulated source vibration at different vibration frequencies ω_m on the T₁ and T₂ MRI image segments of human brain which lead to blurring and ghosting in the MRI image segment are illustrated in Figures 1 and 2. The brain image was acquired at 1 Tesla magnetic field and the impact of Fourier components of the vibrations on magnetic moments were artificially introduced at a computational level in order to demonstrate the impact on image quality. The vibrational effects have a relatively higher impact on overall image quality with an increase in frequency which is well reflected in the image quality.

Discussion

Conclusion

Acknowledgements

References

1. Emsley J.W., Feeney, J. and Emsley, J. W., Feeney, J., & Sutcliffe, L.H. High Resolution Nuclear Magnetic Resonance Spectroscopy (Elsevier, Amsterdam, 2013). Vol. 2.

2. Brown W.F., Thermal fluctuations of a single-domain particle, Phys. Rev. 1963, 130 (5), 1677.

3. Carr, H.Y. and Purcell, E.M., Effects of diffusion on free precession in nuclear magnetic resonance experiments, Phys. Rev. 1954, 94 (3), 630.

4. Woessner, D.E. Brownian motion and its effects in NMR chemical exchange and relaxation in liquids, Conc. Mag. Res. 1996, 8 (6), 397-421.

5.Pipe, J. G. Motion correction with PROPELLER MRI: application to head motion and free-breathing cardiac imaging. Magnetic resonance in medicine, 1999, 42(5), 963-969.

6. Titze, I.R. and Strong, W.J., 1975. Normal modes in vocal cord tissues. The Journal of the Acoustical Society of America, 57(3), pp.736-744.

7. Foerster, B. U., Tomasi, D. and Elisabeth C. Caparelli, E.C. Magnetic field shift due to mechanical vibration in functional magnetic resonance imaging. Magnetic Res. Med. 2005, 54 (5), 1261-1267.