2656
Motion correction of T2*-weighted MRI with consideration of B0 and B1 effect1National Institute of Neurological Disorders and Stroke, National Institutes of Health, Bethesda, MD, United States
Synopsis
T2*-weighted MRI has broad applications in the brain and can provide both functional and (micro) anatomical information. Unfortunately, it has proven rather sensitive to subtle head motion, and the associated changes in B0 and to a lesser extent B1. In this study, the collective impact of pose-dependent B0 and B1 on T2*-weighted gradient echo MRI was investigated. A conjugate-gradient method was utilized for reconstructing MR images collected during variation of head poses.
Introduction
While T2*-weighted MRI is widely used for such applications as BOLD fMRI[1], venography[2], and the measurement of brain iron content[3], it is quite sensitive to image artifacts resulting from head motion, particularly for multi-shot techniques. These factors limit the clinical potential of T2*-weighted MRI, especially at high field (≥3 T). In this study, a conjugate-gradient-based reconstruction was developed for correcting the effect of different head poses and the pose-dependent B0 and B1 in multi-shot 3D gradient-echo (GRE) T2*-weighted MRI at 7 T.Methods
Two healthy subjects were recruited in this study. A 3D slab-selective multi-echo GRE (mGRE) sequence was utilized to acquire the T2*-weighted data, with TR of 40 ms, flip angle of 12ᵒ, field of view of 240x192x80 mm3 and isotropic resolution of 2 mm. Five echoes spaced by 3.5 ms, TEs ranging from 6 to 20 ms, were sampled for mapping B0 field and the phase from a common transmit B1 and local receive B1 field of each channel. The combined effect of the two will be called “B1 field” for short. The experiment was performed on a 7 T MRI scanner (Magnetom, Siemens) with a birdcage transmit and 32-channel receive head RF coil (Nova Medical).
The mGRE data was acquired at various head poses, whose translation and rotation parameters were estimated from inter-scan co-registration of the mGRE magnitude images. The B0 field was calculated using the unwrapped inter-echo phase difference of the last four GRE echoes to reduce the effect of eddy current. The magnitude of B1 field profile was estimated by smoothing the images of each channel after they were divided by a homogenized sum-of-magnitude reference image. The phase of the B1 field was calculated by removing the B0 phase component from the mGRE image phase for each channel.
To mimic the effect of intra-scan motion on image reconstruction, half of the sequential k-space data k, acquired in the echo at 20 ms TE at one pose (P0) was combined with the other half of the k-space data from a different head pose. Based on the conjugate gradient method[4], the following linear equation was solved to reconstruct the image vector ρ:
$$(\bf{FSBM})^H\boldsymbol{\Psi}^{-1}\bf{FSBM}\boldsymbol{\rho}=(\bf{FSBM})^H\boldsymbol{\Psi}^{-1}\bf{k}$$
where M, B, S and F represent the pose-, B0-, B1- and Fourier-encoding matrices, respectively, and Ψ is the noise covariance matrix. The evaluation was carried out in three correction modes: (1) “Full Correction” in which both B1 and B0 information for each head pose was utilized for the corresponding k-space data in the reconstruction, (2) “B1 Correction Off” in which B1 distribution was assumed to be independent of head pose and (3) “Partial B0 Correction” in which the B0 field from the subject was calculated from P0 and assumed to move with the head. For this purpose, the static external field (from magnet and shims) was quantified using a spherical phantom in the experiment of subject #2[5]. The image obtained at P0 was used as the ground truth for evaluating the quality of the images reconstructed from the assembled data.
Results
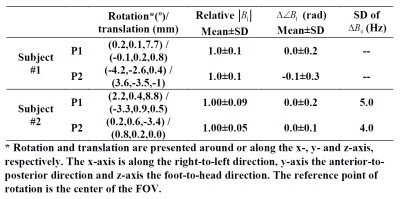
In both subjects, the measured head pose, relative |B1| change, B1 phase difference ($$$\angle{B_1}$$$) and standard deviation (SD) of B0 difference relative to those in P0 are summarized in Table I.
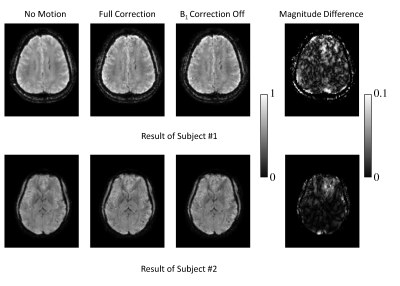
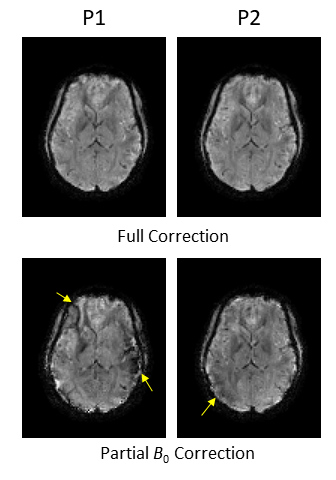
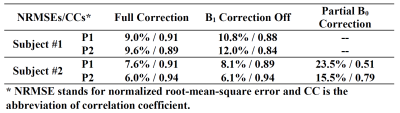
The reconstruction results comparing “B1 Correction Off” and “Full Correction” modes using k-space data assembled from two different head poses are shown in Fig. 1. The image obtained from a reconstruction of k-space data from the P0 scan (“No Motion”) is also shown. With “B1 Correction Off”, the images are slightly degraded both visually and quantitatively (Table II). In subject #2, as can be seen in Fig. 2 and Table II, the effect of B0 correction is more significant than the contribution of B1 correction shown in Fig 1, although the B0 inconsistency between poses only reaches a few Hertz of SD (Table I). The full correction mode in both subjects produced results similar to the ground truth from P0.
Discussion
In this study, a conjugate-gradient-based reconstruction was developed for correcting the effect of head pose, B0 and B1 field change on T2*-weighted MRI acquisition. In the observed scenarios with less than 9ᵒ of rotation and 4 mm of translation, the effect of pose-dependent B1 field is much less significant than the B0 field. However, this effect may be more severe with larger head movement. Data from other subjects have shown average B1 phase shift exceeding 1 rad when the head moved about 1 cm in the z-direction. Future work is needed to thoroughly examine the B1 field variation in the general range of head pose changes and address the issue of B0 field change due to head motion in realistic scanning situations.Acknowledgements
This work was supported by the Intramural Research Program of the National Institute of Neurological Disorders and Stroke.References
[1] S. Ogawa, T. M. Lee, A. R. Kay, and D. W. Tank, “Brain magnetic resonance imaging with contrast dependent on blood oxygenation.,” Proc. Natl. Acad. Sci. U. S. A., vol. 87, no. 24, pp. 9868–9872, Dec. 1990.
[2] R. H. Ayanzen, C. R. Bird, P. J. Keller, F. J. McCully, M. R. Theobald, and J. E. Heiserman, “Cerebral MR Venography: Normal Anatomy and Potential Diagnostic Pitfalls,” Am. J. Neuroradiol., vol. 21, no. 1, pp. 74–78, Jan. 2000.
[3] B. Yao, T.-Q. Li, P. van Gelderen, K. Shmueli, J. A. de Zwart, and J. H. Duyn, “Susceptibility contrast in high field MRI of human brain as a function of tissue iron content,” NeuroImage, vol. 44, no. 4, pp. 1259–1266, Feb. 2009.
[4] J. R. Shewchuk, “An introduction to the conjugate gradient method without the agonizing pain,” 1994.
[5] J. Liu, J. de Zwart, P. Van Gelderen, and J. Duyn, “Motion-induced magnetic field changes inside the brain,” in Proceedings of the 26th Annual Meeting of ISMRM, Honolulu, HI, USA, 2017, p. 1302.
Figures