Synopsis

Preoperative characterization of the renal lesions has clinical significance in determining the appropriate treatment strategy and evaluating prognosis. The current study aims to investigate the potential of multiparametric DWI models, including monoexponential, biexponential, stretched-exponential, and kurtosis models in distinguishing between benign and malignant renal lesions, different tumor types as well as different grading of RCC. Compared with monoexpontial model, these highly parameterized non-Gaussian diffusion models may provide more information in the characterization of renal lesions, which would be helpful in improving therapy strategies and prognoses in the future, and further evaluation are required.

Purpose: Diffusion-weighted imaging (DWI) is an effective and noninvasive technique and apparent diffusion coefficient (ADC) derived from fitting a monoexponential model has been widely used to characterize renal lesions despite its current limitations^{1, 2}. Previous researchers have suggested that advanced fitting models, such as biexponential or stretched exponential DWI models and diffusion kurtosis imaging (DKI) might provide more accurate information about water diffusion³. The purpose of this study was to determine the utility of these multiparametric DWI models in the differentiation and characterization of renal solid masses.

Materials and Methods: This study included 98 patients (23 benign and 75 malignant lesions) who underwent 3T MRI (with diffusion-weighted imaging at b values of 0, 30, 50, 100, 250, 500, 1000 and 2000sec/mm2). Histological subtype and nuclear grade were determined for each malignant lesion. Diffusion model selection was investigated in each lesion using the Akaike information criteria (AIC). Mann–Whitney U-test and receiver operating characteristic (ROC) curves were used for statistical evaluations.

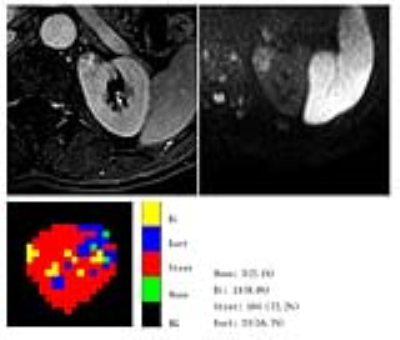
Results: Goodness-of-fit analysis showed that most benign and malignant lesion voxels (65.64% and 53.66%, respectively) were preferred by the stretched-exponential model. ADC, Ds and MK showed significant differences between benign and malignant lesions (P < 0.05), and between low grade and high grade ccRCC. In addition, α were significantly lower in the benign group than in the malignant group (P < 0.05). All diffusion measures showed significant differences between ccRCC and non-ccRCC (P < 0.05) except Df and α (P=0.217 and 0.065, respectively). Results of the diagnostic performance of diffusion parameters in differentiating benign and malignant lesions, ccRCC and non-ccRCC, as well as low and high grade ccRCC, are summarized in Figure 2-4.

Discussion: Goodness-of-fit analysis suggested a stretched exponential model for both benign and malignant renal lesions, indicating that significantly better fitting of the diffusion signals could be achieved by non-Gaussian models. Since the non-Gaussian diffusion models did not reveal significantly superior performance over the conventional ADC for renal cancer detection and subtyping and grading of RCC, the diagnostic value of parameters derived from non-monoexponential diffusion models needs further exploration. Furthermore, as highly parameterized non-Gaussian diffusion models may provide more information in the characterization of renal lesions, which would be helpful in improving therapy strategies and prognoses in the future, and also requires further evaluation.

Acknowledgements

References

References: 1. Zhang, J., Tehrani, Y. M., Wang, L., Ishill, N. M., Schwartz, L. H. and Hricak, H., Renal masses: characterization with diffusion-weighted MR imaging--a preliminary experience, RADIOLOGY, 2008, 247: 458-464.

2. Wang, H., Cheng, L., Zhang, X., Wang, D., Guo, A., Gao, Y. and Ye, H., Renal cell carcinoma: diffusion-weighted MR imaging for subtype differentiation at 3.0 T, RADIOLOGY, 2010, 257: 135-143.

3. Bai, Y., Lin, Y., Tian, J., Shi, D., Cheng, J., Haacke, E. M., Hong, X., Ma, B., Zhou, J. and Wang, M., Grading of Gliomas by Using Monoexponential, Biexponential, and Stretched Exponential Diffusion-weighted MR Imaging and Diffusion Kurtosis MR Imaging, RADIOLOGY, 2016, 278: 496-504.