2450
A Subspace Approach to Accelerated HASTE Acquisition for Fetal Brain MRI1Athinoula A. Martinos Center for Biomedical Imaging, Chalestown, MA, United States, 2Harvard Medical School, Boston, MA, United States, 3Boston Children's Hospital, Boston, MA, United States, 4Electrical Engineering, University of Southern California, Los Angeles, CA, United States, 5Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 6Radiology, Harvard Medical School, Boston, MA, United States
Synopsis
HAlf-fourier Single-shot Turbo spin Echo (HASTE) acquisition is widely used in fetal MR imaging due to its T2 contrast and motion robustness, but speed and T2-blurring remain a problem for fully sampled acquisitions. In the work, we describe a new reconstruction approach based on low-rank and subspace modeling of local k-space neighborhood to accelerate HASTE acquisition. The proposed approach decreases the echo-train length with improved image quality and noise robustness compared to conventional reconstruction. It is compatible with the vendor-provided acquisition. The effectiveness and utility of the proposed approach is evaluated with both retrospectively and prospectively undersampled fetal imaging data.
Introduction
Accelerated HAlf-fourier Single-shot Turbo spin Echo (HASTE) acquisition is widely used in fetal MRI1, since it provides good T2 contrast, and improves motion robustness. Conventional reconstruction approach accelerates HASTE acquisition with a hybrid half-Fourier2 and GRAPPA3 reconstruction. While widely used in clinical practice, it enables only a low to medium acceleration factor before severe noise amplification occurs. Recently, we introduced a low-rank model-based approach to accelerate HASTE4, which utilizes the linear predictability of local k-space neighborhood associated with limited image support. The proposed approach provides better image quality and noise robustness, and is compatible with the standard HASTE acquisition scheme. In this abstract, we extend the early work to investigate an alternative low-rank model, which models slowly-varying image phase. To enhance the computational efficiency, we further incorporate a subspace constraint into the reconstruction process. We demonstrate the effectiveness of the proposed approach on both retrospectively undersampled data and prospectively-undersampled data.Theory
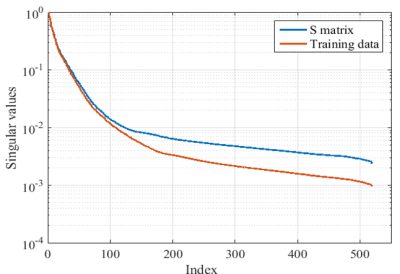
Early work has shown that an approximately low-rank matrix can be constructed by collecting patches of k-space data, if the underlying image has a slow-varying image phase5. Here we form such a data matrix, denoted as $$$\mathbf{S}\in\mathbb{C}^{M\times N}$$$. Moreover, to account for correlation between multi-coil data6, we further form the matrix $$$\mathbf{S}^P = [\mathbf{S^1}, \mathbf{S}^2,\cdots, \mathbf{S}^L]\in\mathbb{C}^{M\times LN}$$$. Here, by enforcing the low-rank property, i.e., $$$\mathrm{rank}(\mathbf{S}^P) \leq r$$$, we can formulate a matrix completion problem that enables reconstruction from sub-Nyquist data. Although directly solving the matrix completion problem often provides good accuracy, it often results in an expensive computational problem. To enhance the computational efficiency, we further introduce a null space constraint7, which pre-estimates the null space of $$$\mathbf{S}^P$$$ from the full-sampled calibration/training data. Figure 1 shows the singular value decays respectively from $$$\mathbf{S}^P$$$ and the calibration data, which follow a very similar trend. More specifically, let the column of $$$\mathbf{V}_s$$$ span the null space of $$$\mathbf{S}^P$$$. Enforcing both the low-rank constraint and the subspace constraint, we can formulate the following image reconstruction problem: $$\hat{\mathbf{z}} =\mathrm{arg}\underset{\mathbf{z} }{\mathrm{~min}}\parallel\mathcal{P}_s(\mathcal{T}(\mathbf{d})+\mathcal{T}^{c}(\mathbf{z}))\mathbf{V}_s\parallel^2_2$$ where $$$\mathcal{T}$$$ is the linear operator that maps the sampled k-space data into the complete k-space data vector, while filling unsampled k-space locations with zeros; $$$\mathcal{T}^c$$$ is the linear operator performing the complementary operation; and $$$\mathcal{P}_s$$$ maps the complete k-space data to the data matrix $$$\mathbf{S}^P$$$. Note that with the subspace constraint, the reconstruction problem reduces to a sparse linear least-squares problem, which can be efficiently solved by a number of numerical algorithms (e.g., the iterative LSQR algorithm).
Methods
We first evaluated the performance of the proposed approach with retrospectively-undersampled data. Here we compared the proposed approach with the conventional reconstruction. More specifically, under an IRB approved protocol, we performed the HASTE acquisition on one healthy pregnant woman at a 3T Siemens Skyra scanner, equipped with 20 coils. Here FOV = 360×360 mm2, slice thickness = 3.5 mm, and matrix size = 256×512. We performed a half-Fourier acquisition covering the 5/8 of the k-space, and then performed a factor of 4 undersampling in the outer k-space. The data acquisition scheme is illustrated in Figure 2. With this acquisition scheme, the net acceleration factor is 3. We compared the proposed approach with the reference obtained from the fully-sampled data, and the conventional approach using the GRAPPA and half-Fourier reconstruction. To evaluate the utility of the proposed approach, we further performed prospectively-undersampled HASTE acquisition of three imaging slices and reconstructed the data using the proposed approach.Results
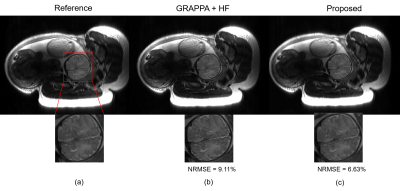
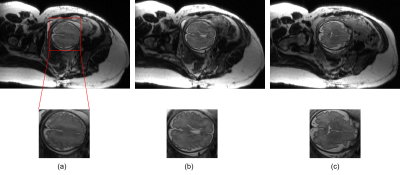
Figure 3 shows the results from the retrospectively-undersampled experiments. As can be seen, the proposed method provides improved image quality compared to the conventional reconstruction approach. In particular, it reduces the noise amplification, while well preserving the anatomical structure of the fetal brain. Figure 4 shows the results from the prospectively-undersampled experiments. As can be seen, the proposed approach consistently provides high-quality reconstructions for all the imaging slices.Conclusion
In this abstract, we developed a new imaging approach to accelerate HASTE acquisition for fetal MRI. The proposed approach enforces the low-rank modeling of local k-space neighborhood, and further incorporates the subspace constraint to simplify the computational problem. We demonstrated the effectiveness of the proposed approach with both retrospectively-undersampled data and prospectively-undersampled data.Acknowledgements
This work was support in part by NIHR01EB017337 and NIH-U01HD087211.References
[1] A. Gholipour, J. A. Estroff, C. E. Barnewolt, R. L. Robertson, P. E. Grant, B. Gagoski, S. K. Warfield, O. Afacan, S. A. Connolly, J. J. Neil, A. Wolfberg, and R. V. Mulkern. “Fetal MRI: A technical update with educational aspirations,” Concepts Magn. Reson. Part A, vol. 43, pp. 237-266, 2014.
[2] D. C. Noll, D. G. Nishmura, and A. Macovski, “Homodyne detection in magnetic resonance imaging,” IEEE Trans. Med. Imag. vol. 10, pp. 154-163, 1991.
[3] M. A. Griswold, P. M. Jakob, R. M. Heidemann, M. Nittka, V. Jellus, J. Wang, B. Kiefer, and A. Haase. “Generalized autocalibrating partially parallel acquisitions (GRAPPA),” Magn. Reson. Med., vol. 47, pp. 1202-1210, 2002.
[4] B. Zhao, Borjan Gagoski, Elfar Adalsteinsson, P. Ellen Grant, and Lawrence L. Wald, “Accelerated HASTE-Based Fetal MRI with Low-Rank Modeling”, In: Proc. Int. Soc. Magn. Reson. Med. 2016; p. 4820.
[5] J. P. Haldar, “Low-rank modeling of local k-space neighborhoods (LORAKS),” IEEE Trans. Med. Imag., vol. 33, pp. 668-681, 2014.
[6] J. P. Haldar and J. Zhuo, “P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data,” Magn. Reson. Med. vol.75, pp. 1499-1513, 2016.
[7] J. P. Haldar, “Autocalibrated LORAKS for fast constrained MRI reconstruction”, in Proc. IEEE Int. Symp. Biomed. Imaging, pp. 910-913, 2015.
Figures