2336
The case for 3D PRESTO fMRI: Improved temporal SNR via ghost suppression by temporal filtering1Biomedical Engineering, University of Michigan, Ann Arbor, MI, United States
Synopsis
We apply a recently-introduced method for more efficient RF-spoiling in dynamic imaging to PRESTO fMRI, and show that this improves temporal SNR significantly. For a whole-brain fMRI acquisition with high temporal resolution (TRvol=0.52s) and 3.3mm isotropic resolution, tSNR is maximized for a net gradient area of only about 1-1.5 cycles/voxel (applied to two gradient axes). We anticipate that the use of such low spoiler gradients will make PRESTO a much more viable alternative for 3D fMRI.
INTRODUCTION
There is an ongoing debate about the relative merit of 3D EPI vs simultaneous multi-slice1 (SMS) imaging for BOLD functional MRI2. Often “forgotten” in this discussion is 3D PRESTO3-4, an efficient sequence for T2*-weighted fMRI that is well suited for rapid 3D multi-shot imaging. In PRESTO, the echo time (TE) exceeds the sequence TR, eliminating the need for a “dead” time for T2* contrast buildup. In addition, 3D imaging has many potential advantages over 2D, including: contiguous voxels, reduced in-flow and other spin-history effects, reduced signal from cerebrospinal fluid (CSF) and hence reduced CSF/cortex partial volume effects, reduced RF power deposition (SAR), and potential for improved image signal-to-noise ratio (SNR) which may enable increased spatial resolution. However, despite its many potential advantages, 3D PRESTO has not become widely adopted. In part this is (likely) due to the sensitivity of segmented sequences to physiological fluctuations which reduces temporal SNR, particularly when TRvol exceeds the heart rate. However, this drawback will become less important as the field moves to higher frame rates5. We suspect that another reason that PRESTO is still mainly used for certain niche fMRI applications is the need for relatively large spoiler gradients, which increase scanner noise and peripheral nerve stimulation (PNS), and makes the sequence more susceptible to flow- and motion-induced signal fluctuations (due to larger first-order gradient moment) which reduces tSNR. For example, to shift the echo into the following TR (1-echo shifting), two gradient lobes with area −A and 2A , respectively, are required for a net zero-order moment A in each TR interval (Fig. 1(a)). It is therefore necessary to balance the competing needs for good spoiling, achieved by increasing A, and reduced sensitivity to flow/motion and PNS as well as reduced TR, which requires decreasing A. Here we apply a recently introduced method for more efficient RF-spoiling6 to 3D PRESTO, to investigate whether this can improve tSNR and reduce the required spoiler gradient size A, thus making PRESTO a more viable option for fMRI. We also compare the resulting tSNR against a matched SMS sequence.METHODS
We obtained 3D PRESTO resting-state fMRI data in five volunteers on a 3T GE scanner with a 32-channel receive array, using stack-of-spirals imaging with 3- and 1.8-fold undersampling in kx-ky and kz, respectively (Fig. 1(a)) [3.3 mm isotropic resolution; 72x72x54 matrix; TE/TR/TRvol=32/20/523 ms; acquisition bandwidth ±125kHz; flip angle 10o]. We repeated the scan several times, varying the spoiler gradient size A. We reconstructed a 3D image volume at each temporal frame using iterative non-Cartesian SENSE with nuFFT and mild total variation regularization, implemented with the Image Reconstruction Matlab toolbox7.
In Ref. 6 it was shown that by careful choice of the RF spoiling increment Φ and the acquisition matrix, the “ghost” signal (due to imperfect RF spoiling) across subsequent frames will oscillate at the sampling (Nyquist) frequency 1/(2×TRvol). The ghost signal can then be suppressed by applying a notch filter at the Nyquist frequency. In this work we used Φ = 150o, 30 excitations (shots) per TRvol, and the notch filter shown in Fig. 2(a). We applied the filter to the (complex) image time-series. In three of the volunteers we also obtained SMS EPI data with similar spatio-temporal resolution [3.3 mm isotropic resolution; matrix 72x72x42 matrix; multi-band factor 6; TE/TRvol = 32/530 ms; acquisition bandwidth ±250 kHz; flip angle 44o]. SMS images were reconstructed using a vendor-provided algorithm.
RESULTS
Figure 3 shows that applying the temporal filter technique from Ref. 6 improves tSNR for all values of A in the observed range (0.5 to 2.0 cycles/voxel). Moreover, the temporal SNR peaks at a typical value of only about 1-1.5 cycles/voxel (applied along two gradient axes), likely reflecting an optimal tradeoff between spoiling efficiency and sensitivity to flow/motion. Similar results were obtained in the other volunteers (not shown).
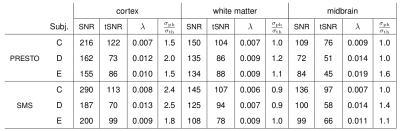
Table 1 summarizes SNR and tSNR measurements using PRESTO and SMS, in three volunteers. The reported values are based on the definitions $$$ tSNR=\sqrt(\sigma_{th}^2 + \sigma_{th}^2)$$$ and $$$\sigma_{ph} = \lambda S$$$, where $$$\sigma_{th}$$$ and $$$\sigma_{th}$$$ are the thermal and physiological noise standard deviations, S is the mean time-course signal, and $$$\lambda$$$ is a proportionality constant to be determined. We observe that tSNR is approximately equal for 3D PRESTO and SMS, in all three regions.
CONCLUSION
Applying the ghost reduction technique in Ref. 6 to dynamic 3D PRESTO imaging improves tSNR significantly for a given spoiler gradient area A. In addition, applying this ghost suppression technique reduces the gradient area A that maximizes tSNR. Taken together, our results indicate that for whole-brain fMRI with high temporal resolution (~0.52 sec), 3D PRESTO can be an attractive alternative to SMS.Acknowledgements
This work was supported by NIH grants R01EB023618 and R21EB019653.References
1. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med 2012;67:1210–1224.
2. Stirnberg, R, Huijbers, W, Brenner, D, Poser, BA, Breteler, M, Stöcker, T. Rapid whole-brain resting-state fMRI at 3 T: Efficiency-optimized three-dimensional EPI versus repetition time-matched simultaneous-multi-slice EPI. Neuroimage 2017;163:81-92.
3. Moonen CT, Liu G, van Gelderen P, Sobering G. A fast gradient-recalled MRI technique with increased sensitivity to dynamic susceptibility effects. Magn Reson Med 1992;26:184–189.
4. van Gelderen P, Duyn JH, Ramsey NF, Liu G, Moonen CT. The PRESTO technique for fMRI. Neuroimage 2012;62:676–681.
5. Lee HL, Zahneisen B, Hugger T, LeVan P, Hennig J. Tracking dynamic resting-state networks at higher frequencies using MR-encephalography. Neuroimage 2013;65:216–222.
6. Nielsen JF, Noll DC. Improved spoiling efficiency in dynamic RF-spoiled imaging by ghost phase modulation and temporal filtering. Magn Reson Med 2016;75:2388–2393.
7. http://www.eecs.umich.edu/∼fessler
Figures
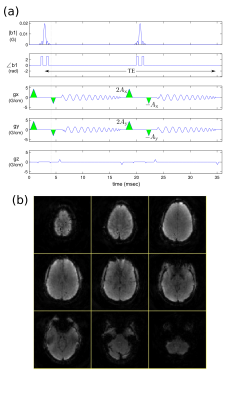
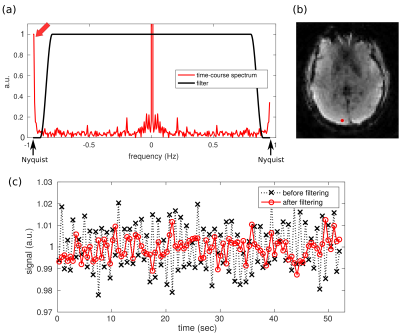
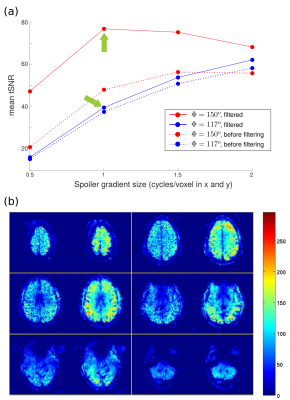
Fig. 3. Results obtained in one of the five volunteers. (a) Dependence of tSNR on spoiler gradient size, both before (dotted lines) and after (solid lines) temporal filtering. Results are also shown for Φ=117o, an acquisition choice that does not cause the unwanted ghost signal to oscillate at the temporal Nyquist frequency (as required by Ref. 6). (b) tSNR maps for the points indicated by the green arrows in (a).