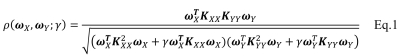Introduction

Single voxel analysis with Gaussian smoothing (SV) can improve the signal-to-noise ratio of fMRI data, but it also introduces spatial blurring of activation patterns, leading to poor specificity [1]. To adaptively model the shapes of activation patterns, local canonical correlation analysis (local CCA) was proposed for fMRI data analysis [2, 3]. Local CCA, however, could handle only 2D applications by using in-plane 2D spatial neighborhoods instead of 3D neighborhoods because of computational time requirement for 3D neighborhoods. Also, local CCA needs constraints on the spatial basis functions to increase the specificity of the method. In this study, we have implemented an efficient sequential quadratic programming (SQP) algorithm to solve the 3D local constrained CCA problem. We also propose a novel global kernel CCA method to analyze the time series of the whole brain simultaneously. All these analysis methods were evaluated on episodic memory task fMRI data acquired from normal controls and amnestic mild cognitive impairment (aMCI) subjects.

Method

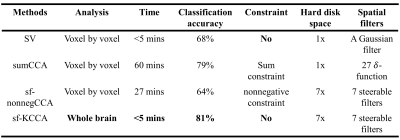
Subjects: Episodic memory task fMRI data of 7 NCs and 7 aMCI subjects were acquired on a 3.0T GE MRI scanner. The entire task consisted of six periods of encoding, distraction, recognition and instruction periods. Analysis: Along with the conventional SV method, two local CCA methods, including sumCCA and sf-nonnegCCA, and the proposed global kernel CCA method (sf-KCCA) were used. The sumCCA method uses 27 3D $$$\delta$$$-functions on 3 x 3 x 3 voxel neighborhoods whereas the sf-nonnegCCA and sf-KCCA use a set of steerable filters [4] to model activations. Local CCA methods require spatial constraints to avoid overfitting. Specifically, sumCCA requires the weight of center voxels greater than the sum of the weights of neighboring voxels (called sum constraint) and sf-nonnegCCA requires the weights of filtered time series to be nonnegative. We developed a SQP algorithm to efficiently solve sumCCA and sf-nonnegCCA. The proposed global sf-KCCA method uses KCCA with regularization parameter $$$\gamma$$$ [5] to maximize the correlation between design matrix $$$X$$$ and the whole brain time series filtered by steerable filters $$$Y$$$. The correlation is defined as in Eq.1, where $$$K_{XX}=XX^T$$$ and $$$K_{YY}=YY^T$$$. The parameter $$$\gamma$$$ controls overfitting and is selected to maximize the correlation difference between active-state data and wavelet-resampled null data. sf-KCCA does not require any spatial constraint and can be solved as a standard eigenvalue problem. The weight of oriented filters at voxel $$$q$$$ can be computed as $$$\alpha_q=Y^T_q\omega_Y$$$ and then the coefficient of the design matrix $$$\beta_q$$$ can be solved as a least square problem by minimizing $$$||X\beta_q-Y_q\alpha_q||_2$$$. A brief comparison of these four analysis methods is shown in Table 1. The F statistic was used to construct activation maps for all of the analysis methods we compared. A receiver operating characteristic (ROC) estimation method [6] was used to evaluate the detection accuracy of different analysis methods. A radial basis function (RBF) classifier was applied for group classification with input features as the percentage of activated voxels in hippocampal subregions at significance levels 10^-3, 10^-4 and 10^-5.

Results

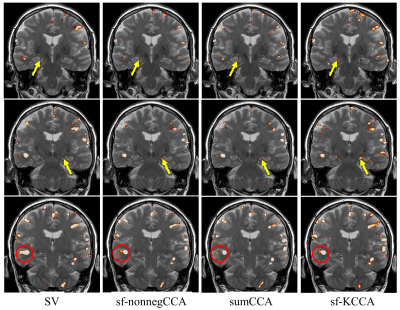
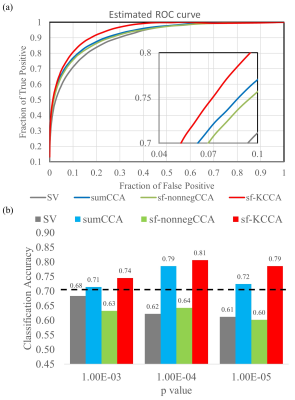
Fig.1 shows the seven steerable filters used in sf-nonnegCCA and sf-KCCA, which consist of one isotropic Gaussian filter and six oriented filters. Fig.2 shows the F statistic activation maps for contrast “encoding – distraction” at $$$p$$$ value 10^-4. The activation map for SV shows strong blurring of activation patterns into white matter or CSF regions, whereas for the other methods spatial blurring is reduced (compare activations in red circle). Furthermore, sf-KCCA detects the strongest activation pattern in the hippocampus, as marked by a yellow arrow. Fig.3a shows that sf-KCCA has the largest area under the ROC curve, which indicate that sf-KCCA can most accurately detect activations. Furthermore, we have classified subjects as aMCI or NCs using a RBF method, and the proposed sf-KCCA achieves the best group discrimination.

Conclusion

In this study, the 2D local constrained CCA problem was extended to 3D for fMRI data analysis and solved with an efficient SQP algorithm. In addition, a 3D global spatially-adaptive KCCA method was proposed. This novel sf-KCCA method outperformed local CCA methods and univariate methods in detecting brain activation, especially in small regions such as the hippocampus and its subfields. Unlike local CCA methods requiring spatial constraints and CPU time, the global sf-KCCA method achieves highest classification accuracy and is the most computationally efficient method and does not need spatial constraints.

Acknowledgements

The study is supported by the National Institutes of Health (grant number 1R01EB014284 and P20GM109025).