Introduction

Data analysis in fMRI usually consists of a two level model where the 1^st level detects the effect of each individual subject and the 2^nd level makes group-inferences¹. In the 2^nd level analysis, summary statistics and combining hypothesis tests such as Fisher’s data fusion are most widely used^2,3,4. These univariate methods assume independent neighboring voxels and are not sensitive enough for data with low signal-to-noise ratio. Multivariate canonical correlation analysis (CCA) has been applied in fMRI 1^st level analysis and has been shown to improve sensitivity in activation detection^5,6. In this study, we introduce a multivariate CCA model to incorporate neighboring voxels in fMRI 2^nd level analysis to obtain more accurate group activation maps and group activation difference maps.

Methods

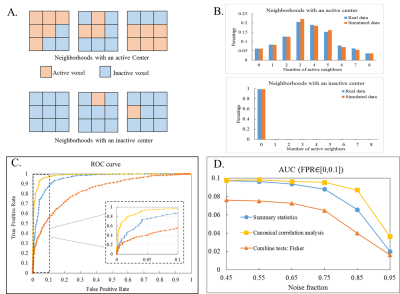
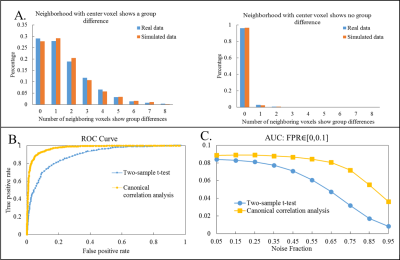
Model: The 1^st level model in fMRI can be written as y=Xβ+ε, where vector y represents time course from a single voxel, X represents functions used to model the BOLD response, and β is the subject effect. The 2^nd level CCA is then modeled as Bα_G=X_Gβ_G+ε_G, where B=(β₁,β₂,...,β_m)(size: Nxm) is a matrix that represents 1^st level effects of m voxels in a local neighborhood (m= 9 for a 3x3 neighborhood) from N subjects, and X_G (size: Nx1or2) is the design matrix modeling either within-group activation detection (X_G=[1,...,1]^T) or between-group difference detection (X_G=[1,...,1,0,...,0;0,...,0,1,...,1]^T ). Using CCA, local weighting coefficient α_G for the neighborhood and group inference β_G for the centering voxel are found by maximizing the canonical correlation coefficient between Bα_G and X_Gβ_G. With a proper normalization term, the solution of maximizing the correlation is equivalent to minimizing the variance of the error term ε_G^Tε_G. Statistical analysis: Wilk’s lambda statistics is used to determine the group inference of the center voxel for a specific contrast c (c=1 for within-group activation detection and c=[1,-1]^T for between-group difference detection). Statistical thresholds for significance are computed from the null distribution non-parametrically (see Table. 1). Imaging: fMRI data (TR/TE/resolution=2s/30ms/1.7x1.7x5mm³, 25 slices, coronal oblique, 288 time frames) from 8 normal subjects and 8 MCI subjects each consisting of a resting-state data set and a memory task data set were analyzed. The memory task involved viewing faces paired with occupations and contained instruction, encoding, recognition and control (distraction) periods. Validation with Simulated data: 1000 3x3 neighborhoods with active center voxels and 1000 neighborhoods with inactive center voxels for 16 subjects were simulated. The distribution of active neighbors in each local neighborhood followed the empirical distribution of real fMRI data analyzed with the summary statistics method. Time courses for simulated neighborhoods were obtained from neighborhoods in real data with the same activation patterns (both resting-state and task fMRI). Specifically, wavelet-resampled resting-state time courses were added to the task time-series with different noise fractions to simulate time courses at different noise levels. Both univariate and multivariate techniques were applied to the simulated data and receiver operating characteristic (ROC) method was used to evaluate the performance of each method. Validation with real data: Standard mass-univariate method was applied in fMRI 1^st level analysis and a voxel-wise effect map of contrast encoding v/s control was computed for each subject. Both univariate and multivariate techniques were applied to the 2^nd level analysis. Both within-group activation map and between-group difference map were computed.

Results

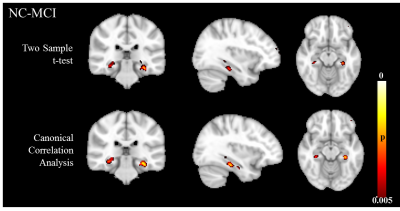
Table. 1 summarizes the univariate and multivariate methods applied in the 2^nd level analysis. Results from simulation are shown in Fig.1 (within-group activation detection) and Fig.2 (between-group difference detection). Area under the ROC curves (AUC) at multiple noise levels demonstrate optimum performance of the proposed CCA methods, especially at high noise levels. Whole brain within-group activation map for real fMRI data with contrast encoding v/s control is shown in Fig.3 (p<0.001, uncorrected) and between-group difference map (NC-MCI) for the same contrast is shown in Fig. 4 (p<0.005, uncorrected). Improved activations are observed in fusiform gyrus (Fig. 3) and larger between-group differences are seen in hippocampus (Fig. 4) using multivariate CCA method, as compared to the univariate summary-statistics. Further, when compared to the fisher’s data fusion technique in detecting within-group activations, multivariate CCA method detects less false positives (Fig. 3).

Discussion and Conclusion

We have introduced a multivariate CCA method to incorporate local neighboring voxels in fMRI 2^nd level analysis. Using simulation, we demonstrated better performance in both activation and difference detection of the proposed method over univariate techniques. Applying the proposed method to real fMRI episodic memory data, larger within-group activation in fusiform gyrus and stronger between-group differences in hippocampus were found.

Acknowledgements

The study is supported by the National Institutes of Health (grant number 1R01EB014284 and P20GM109025).