Introduction

Empirical Mode Decomposition (EMD)^1,2,3 was used as a data-driven method to study the natural occurring frequency bands of resting-state data, and specifically investigate energy-period relationships of Intrinsic Mode Functions (IMFs) for resting-state networks. The novelty of the current approach lies in the data-adaptive and user-independent decomposition of fMRI data using the Hilbert-Huang Transform and identification of networks based on characteristic data-driven energy-period signatures of IMFs.

Methods

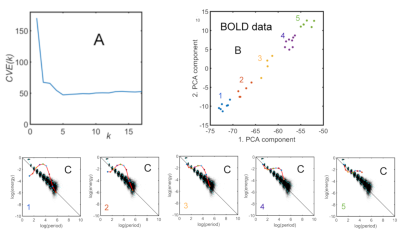
FMRI was performed on 22 healthy subjects in a 3T Siemens MRI scanner equipped with a 32-channel head coil using multiband EPI with imaging parameters: MB8, TR 765ms, TE = 30ms, flip 44deg, partial Fourier 7/8 (phase), FOV = 19.1 x 14.2 cm, 80 slices in oblique axial orientation, resolution 1.65mm x 1.65mm x 2mm, BW =1724 Hz/pixel, 2380 time frames (30min scanning duration). After the usual preprocessing steps all voxels were resampled to a 2mm x 2mm x2mm grid. Group ICA (based on the FastICA algorithm⁴) was performed by stacking all data in the temporal domain and 30 resting-state networks were computed. The group time series signatures of all ICA networks were obtained and further decomposed by EMD into 9 IMFs. The mean energy per unit time and the mean period were computed for each IMF of all ICA components. Energy and period of all IMFs can be considered as a feature vector of each ICA component. We used k-means clustering on all feature vectors, ran cross- validation using the leave-one-out method and determined the optimal number of clusters. Using Principal Component Analysis (PCA) we plotted all 30 ICA time signatures in a 2-dim plot spanning the major principal components. To compare EMD results, we also generated artificial Gaussian noise data (1000 time series, TR 765ms, 30 min duration) using 3 different AR(1) processes. Energy-period plots were then generated for all noise processes and compared with fMRI resting-state signatures.

Results

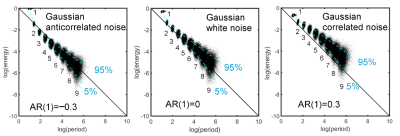
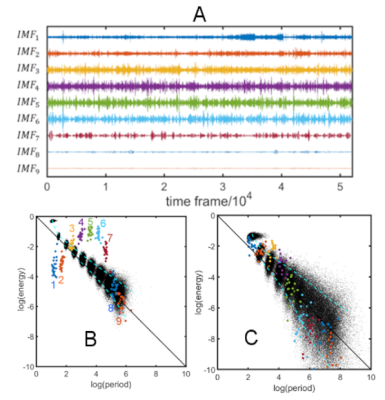
Fig.1 shows the energy-period relationship for different noise processes. All energy-period data points belonging to a specific IMF form an oval-shaped cluster of points. Note that with increasing AR(1) coefficient, the energy-period spectrum is shifted upwards for IMFs 2-9, whereas for IMF1 the shift is downwards towards the diagonal line. The blue dotted lines represent the 5 and 95 percentile of the energy-period distribution for all IMFs. Fig.2A shows the results for the fMRI resting-state data for the Default mode Network (DMN) time signature using EMD. The top portion shows the temporal decomposition into 9 IMFs. The bottom portion (Fig. 2B) shows the energy-period relationship of the IMFs superimposed on the white noise spectrum (black dots). Note the characteristic inverted V shape of the fMRI signal characteristic. For comparison, we show similar resting-state data but collected with a larger TR (TR 2.4s) leading to a spread of the noise component and no characteristic shape of the energy-period signature of the DMN. Here, all signal components are within the 5 to 95 percentile of the noise distribution. Fig.3 shows the results of the K-means clustering of all energy-period feature vectors overlaid on white noise data. The cross-validation error leads to an optimum cluster size of 5 (Fig.3A). Fig. 3B shows the partitioning of all 30 ICA time signatures into 5 clusters. Fig. 3C shows the corresponding mean energy-period profiles of the 5 clusters.

Discussion

The energy-period relationship of the fMRI IMFs provides characteristic signatures that have the shape of an inverted V and are quite different from Gaussian white noise properties. In general, the intermediate IMFs bulge out above the diagonal white noise line defined by log(E)+log(T)=0 and signify networks with strong autocorrelations. Clustering of the shape of these energy-period signatures leads to well-defined ordering of ICA components. We obtained 5 major clusters and were able to rank each network component according to the form of the energy-period relationship by PCA. It is interesting to see that cluster 1, containing 7 ICA components, has the largest signature difference from white noise. These components consist of visual networks, DMN, fronto-parietal networks and auditory network. The clusters further away from cluster 1 (the extreme case is cluster 5) contain higher frequency networks with cerebellar and subcortical features and a signature closer to the white noise energy-period line.

Conclusion

We have studied resting-state networks using EMD to obtain energy-period information. IMFs and associated spatial maps provide a data-driven decomposition of resting-state networks. We found that the IMFs of resting-state networks showed characteristic inverted V-shaped energy-period signatures that allows a natural ranking of all resting-state networks when compared to signatures of white noise.

Acknowledgements

This research project was supported by the NIH (COBRE grant 1P20GM109025 and 1R01EB014284).