Synopsis

Magnetic resonance electrical property tomography (MREPT) is a technology for noninvasively reconstructing electrical properties (EPs) (permittivity, e, and electrical conductivity, s) of the human body from B1-map from MRI. Boundary inaccuracy and noise sensitivity are two problems of most MREPT methods. Previous studies showed that regularization can be one solution for both of the problems. However, there have been few reports on how to set up regularization terms. In this study, we show how region-specific regularization can achieve higher accuracy and noise tolerance.

Synopsis

Magnetic resonance electrical property tomography (MREPT) is a technology for noninvasively reconstructing electrical properties (EPs) (permittivity, $$$ε$$$, and electrical conductivity, $$$σ$$$) of the human body from B1-map from MRI scanning. Boundary inaccuracy and noise sensitivity are two problems of most MREPT methods. Previous studies showed that regularization to convection-reaction MREPT (crMREPT) can be one solution for both of the problems. However, there have been few reports on how to set up regularization terms. In this study, we show how region-specific regularization can achieve higher accuracy and noise tolerance.

Introduction

Magnetic resonance electrical property tomography (MREPT) is a technology for noninvasively reconstructing electrical properties (EPs) (permittivity, $$$ε$$$, and electrical conductivity, $$$σ$$$) of the human body from B1-map from MRI scanning. Boundary inaccuracy and noise sensitivity are two problems of most MREPT methods. Viscosity type regularized MREPT1, could be a solution for both the problems. It could significantly improve the accuracy of the reconstructed EPs, and decrease the sensitivity to noise compared with convection-reaction MREPT (crMREPT)2 which numerically solves a partial differential equation derived from the Maxell’s equations. Regularization is a useful technique for solving ill-posed inverse problems. However, there have been few reports on how to set up the regularization terms for specific problems. In this work, we show how region-specific regularization can achieve higher accuracy and noise tolerance.

Methods

In the study, B1-maps at 128 MHz (3T MRI) were obtained by simulating a double-layered cylindrical phantom (Fig. 1 with details labelled) illuminated by a 16-rung high pass birdcage coil using COMSOL. Different pairs of EPs were assigned to the inner and the outer layers. The table in Fig. 1 (c) lists a number of combinations . The stabMREPT1 (Eq.1), where r is the coefficient for the viscosity-type regularization, was then solved with both region-independent and region-specific $$$ρ$$$ values for different areas of the boundary in question. Note when the region-specific regularization was explored, $$$ρ$$$ is a 2D or 3D vector for two and three regions, respectively. In this case, 1D $$$ρ$$$ means region-independent regularization. Fig. 1 (d) shown two different regions that different $$$ρ$$$’s are applied, the boundary region surrounded by dotted lines and the rest.

Results

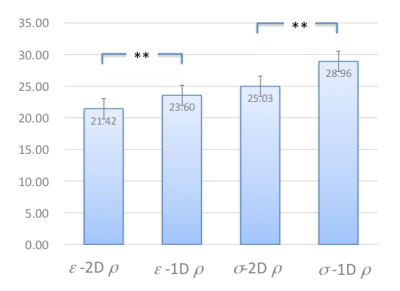
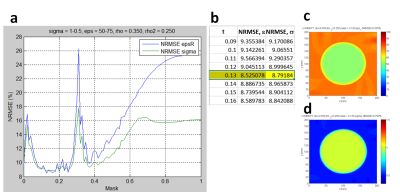
Figure 2 shows the reconstructed EPs, and the explored 2D $$$ρ$$$-NRMSE (Normalized Root Mean Squared Error) space. It is clear that the 2D $$$ρ$$$ resulted in a smaller minimal NRMSE than the 1D $$$ρ$$$ regularization, for the phantom shown in the figure 1 (a). 3D $$$ρ$$$, was also probed in which the $$$ρ$$$ for inner cylinder and outer cylinder apart from the around-boundary ring was set to different values $$$ρ$$$1 and $$$ρ$$$3, for exploration. As a result, $$$ρ$$$1=$$$ρ$$$3 gave the minimal NRMSE. Figure 3 shows a comparison between 2D-$$$ρ$$$ and 1D-$$$ρ$$$ regularization in terms of NRMSE of EPs for 36 phantoms. As shown in the figure, for both $$$ε$$$ and $$$σ$$$, the 2D $$$ρ$$$ led to a better reconstruction, with a significant difference. Figure 4 shows the results of an exploration of the size of the ring 2t, t is a ratio of the inner radius. Figure 4 (a) shows the NRMSE versus t for the reconstructed eps and sigma. As shown, there is a minimum value which lies at t = 0.13. At t = 0.13, the reconstructed EPs are shown in Figure 4 (c) and (d), respectively. When the noise level is SNR=60dB, there exists 2D $$$ρ$$$ which can lead to a smaller NRMSE than 1D $$$ρ$$$.

Discussion

The current work is an approach based on the hypothesis that, the area around the boundary need a specific regularization than the non-boundary area. The results showed that, the boundary-relevant region-specific regularization showed better performance than the regularization with identical coefficient. In future, we will explore the possibility to identify the optimal regularization for more complex boundary morphology with machine learning technology, for the real application, such as, medical diagnosis for cancer tissues based on EP contrasts.

Conclusion

Acknowledgements

References

[1] Changyou Li, Wenwei Yu, and Shao Ying Huang, An MR-Based Viscosity-Type Regularization Method for Electrical Property Tomography (2017) TOMOGRAPHY.ORG, 3, 1, 50-59

[2] Hafalir F, Oran O, Gurler N, et al. Convection-reaction equation based magnetic resonance electrical properties tomography (cr-MREPT). IEEE Trans. Med. Imag. 2014; 33(3): 777-793.