2250
A Novel Phase-unwrapping Method by Using Phase Jumps Detection and Local Polynomial Surface Fitting: Application to Dixon Water-Fat MRI1School of Automation Engineering, University of Electronic Science and Technology of China, Chengdu, China, 2Guangdong Provincial Key Laboratory of Medical Image Processing, School of Biomedical Engineering, Southern Medical University, Guangzhou, China, 3Philips Healthcare, Guangzhou, China
Synopsis
Current phase-unwrapping algorithms are generally challenged by severe noise, rapid-varying phase or disconnected regions. We present a novel phase-unwrapping method by using phase jumps detection and local polynomial surface fitting. The proposed method first segments the whole phase map into blocks by exploiting the phase jumps that are automatically identified. Intra-block wrapping may still exist if the true phase difference between adjacent pixels exceeds π inside a block. To address potential intra-block wraps, we further segment each block into subblocks using the phase partition method, and perform inter-subblock unwrapping using the block-growing method. Simulation and in vivo Dixon water-fat separation experiments were implemented to evaluate the performance of the proposed method, with comparisons to PRELUDE and CLOSE. This method has great potential in phase-related MRI applications in practice.
Introduction
Robust phase-unwrapping is of vital importance with application for Dixon water-fat separation1 and quantitative susceptibility mapping2. However, phase-unwrapping remains challenging due to severe noise, rapid-varying phase or disconnected regions. In this work, we present a novel phase-unwrapping method for Dixon water-fat separation by using phase jumps detection and local polynomial surface fitting (LPSF).
Methods
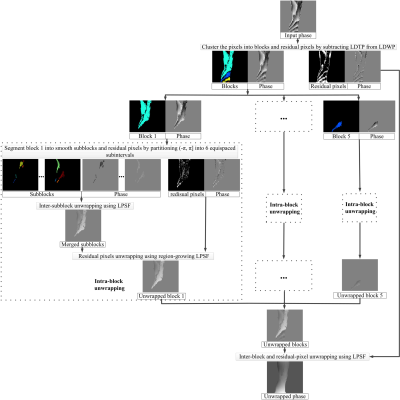
The proposed algorithm: The local difference of phasor reflects the local variation of true phase (LDTP), and is theoretically less than or equal to the local difference of wrapped phase (LDWP)3. As shown in Figure 1, the proposed method first clusters the pixels into blocks and residual pixels by exploiting the phase jumps that are detected by the nonzero difference between LDWP and LDTP. Thereafter, the proposed method sequentially performs intra-block, inter-block and residual-pixel unwrapping. For intra-block unwrapping, the proposed method first segments each block into subblocks using phase partition approach, and then clusters small subblocks into residual pixels. Thereafter, the proposed method sequentially performs inter-subblock and residual-pixel unwrapping using the LPSF approach. The inter-subblock phase-unwrapping starts with the largest subblock, and proceeds with the closest subblock. The variance of the second-order partial derivatives4, 5 as a quality criterion is combined with stack technique to optimize the unwrapping path of residual pixels. The inter-block and residual-pixel unwrapping in the whole phase map are similar to the inter-subblock and residual-pixel unwrapping inside a block.
The extension of the proposed method from 2D to 3D is straightforward. The LDWP, LDTP and quality map are calculated using a 26-neighborhood window, the voxels are grouped into 3D blocks, and the underlying true phase was approximated by a 3D LPSF model. Subblocks are limited within plane to avoid that a single subblock includes two areas where true phase differs by more than 2π. The proposed method was performed on simulation and in vivo Dixon water-fat separation data, with comparison to phase region expanding labeler for unwrapping discrete estimates (PRELUDE)6 and (phase-unwrapping algorithm based on pixel clustering and local surface fitting ) CLOSE3, 7.
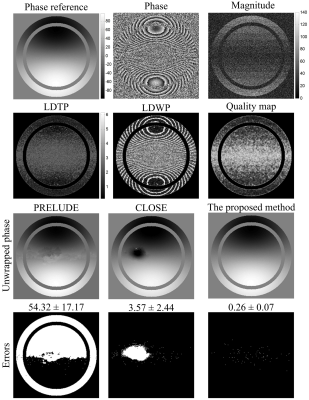
Simulations: In simulation experiment, the magnitude of simulation data was created with 13 sectors. The magnitude of sectors first decreased from 70 to 10, and then increased to 70 with an interval of 10. The phase is obtained by the following formulas8:
$$phase= 500\times \left ( \frac{x}{256}-0.5 \right )\times exp(-5\times ((\frac{x}{256}-0.5)^{2}+(\frac{y}{256}-0.5)^{2}))$$
Zero-mean Gaussian noise with a SD of 20 was added to the real and imaginary parts of the synthesized complex data.
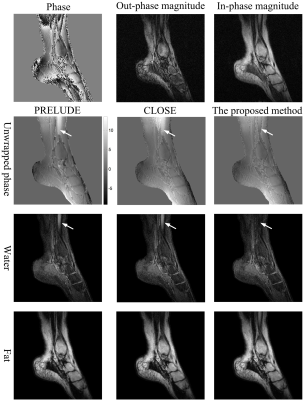
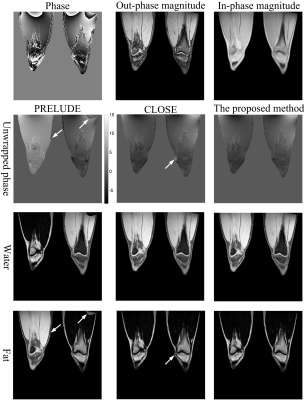
In vivo study: The 3-point Dixon water-fat separation datasets1 were acquired on a 0.35T permanent magnet MR scanner (Xingaoyi Company, Ningbo, China) from 13 volunteers with following parameters: TR/TE = 580/28 ms, FOV = 240×240 mm2, matrix size = 256×256, 10 slices for sagittal and transverse knee, and 5 slices for sagittal ankle. Additionally, the two-point Dixon 3D knee water-fat separation datasets9 were acquired on a 3.0T MR scanner (Philips, Achieva, The Netherlands) from 6 volunteers with following parameters: TR/TE1/TE2 = 20/1.15/2.30 ms, voxel size = 1.36×1.36×3.0 mm3, matrix size = 256×256×30. The unwrapped images are exploited in 2- or 3-point Dixon techniques to generate water and fat images.
Results
Figure 2 shows the unwrapped results of the simulation using the three methods. The results generated by the proposed method have no obvious residual wraps, and the mean and SD of misclassification ratio is 0.26 ± 0.07%.
The representative phase-unwrapping and water-fat separation results of a sagittal ankle slice in the 0.35 T in vivo Dixon water-fat datasets are shown in Figure 3. Figure 4 shows the unwrapped images and water-fat separation results of a representative coronal slice in the 3.0 T 3D knees data. No obvious residual wraps and water-fat swaps are found in the results produced by the proposed method. Among all subjects studied, the number of slices with swaps produced by PRELUDE and CLOSE are separately 194 and 39, while that produced by the proposed method is 9 out of the total knee and ankle images.
Discussion
This work presents a phase-unwrapping method by using phase jumps detection and LPSF. The proposed method realizes phase-unwrapping by exploiting the region-growing LPSF approach, which is insensitive to noise and can acquire accurate unwrapped results even when adjacent true phase difference exceeds π. Additionally, the variance of the second-order partial derivatives as a quality criterion is combined with stack technique to improve the unwrapping path of residual pixels, and this will reduce error propagation and accumulation.
Conclusion
The simulation and in vivo Dixon water-fat separation results demonstrate that the proposed method can accurately unwrap the phase data even in the presence of severe noise, rapid-varying phase and disconnected regions. This method will benefit phase-related MRI applications such as Dixon water-fat separation.Acknowledgements
No acknowledgement found.References
1. Glover G, Schneider E. Three-point Dixon technique for true water/fat decomposition with B0 inhomogeneity correction. Magn Reson Med 1991; 18(2):371-383.
2. Haacke E M, Liu S, Buch S, et al. Quantitative susceptibility mapping: current status and future directions. Magnetic resonance imaging, 2015, 33(1): 1-25.
3. Cheng J, Mei Y, Liu B, et al. A novel phase-unwrapping method based on pixel clustering and local surface fitting with application to Dixon water–fat MRI. Magn Reson Med 2017.
4. Ghiglia DC, Pritt MD. Two-dimensional phase unwrapping: theory, algorithms, and software: Wiley New York; 1998.
5. Zhou K, Zaitsev M, Bao S. Reliable two-dimensional phase unwrapping method using region growing and local linear estimation. Magn Reson Med 2009; 62(4):1085-1090.
6. Jenkinson M. Fast, automated, N-dimensional phase-unwrapping algorithm. Magn Reson Med 2003;49(1):193-197.
7. Cheng J, Liu B, Mei Y, et al. A Robust 3D Phase Unwrapping Method with Application to Quantitative Susceptibility Mapping. The 25th ISMRM (Hawaii, America): 2951, 2017.
8. Dalmau O, Rivera M, Gonzalez A. Weighted robust Basis Function for phase unwrapping. Optics and Lasers in Engineering 2015; 69:13-19.
9. Coombs BD, Szumowski J, Coshow W. Two-point Dixon technique for water-fat signal decomposition with B0 inhomogeneity correction. Magn Reson Med 1997; 38(6):884-889.
Figures