2245
Investigating the Effect of Rapid Exchange Rate on the Accuracy of the Bayesian CEST Model at 7T1Wellcome Centre for Integrative Neuroimaging, FMRIB, University of Oxford, Oxford, United Kingdom
Synopsis
The Bayesian model-based approach has shown a remarkable ability to accurately characterize the APT-CEST effect in vivo. However, no studies have been performed to ensure this performance is maintained when examining labile protons exchanging at faster exchange rates. Here, we examine how exchange rates in the intermediate-to-fast exchange regime affect the characterization of the CEST effect by a model-based approach, and compare it with the MTRasym measurement. The results suggest that the Bayesian model accurately characterizes the CEST effect in question at exchange rates up to 2000 Hz, and outperforms the MTRasym when faced with multiple confounding pools.
Introduction
Chemical Exchange Saturation Transfer (CEST) is an MRI technique sensitive to the presence of low concentration mobile protons exchanging with water, such as the backbone amide protons of proteins. Recently, a Bayesian inference model (BayCEST) has been developed, which has been shown to accurately characterize slow-exchanging species such as amides1. However, this model has not been extensively tested for faster exchanging species, such as amine and hydroxyl molecules. In this work, we investigate the ability of BayCEST to accurately quantify the CEST effect arising from fast-exchanging species up to 2000 Hz.Methods
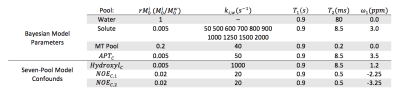
All analyses were performed in MATLAB (Mathworks, Natick, MA). Several sets of Monte Carlo simulations (100 trials in all cases) with an SNR of 100 were performed by numerically simulating the Bloch-McConnell equations over a range of exchange rates from 50 Hz to 2000 Hz for a CEST effect at 3 ppm, with a concentration relative to water of 0.5%. In all cases, the data were generated at 7T using a 2 second pulse train of 25 ms Gaussian pulses with a 50% duty cycle. Each pulse had a maximum amplitude of 4 µT to maximize sensitivity to fast-exchanging species. The CEST pulse train was followed by a 2 second readout, for a TR of 4 seconds. Data was generated for offsets spaced equally between ±5 ppm, with an additional reference scan at 100 ppm.
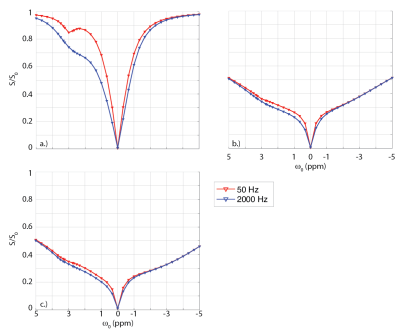
First, a two-pool CEST model was simulated to determine how the model would behave under ideal conditions (i.e. only water and a single solute), and the resulting spectra were fit over all exchange rates to estimate the exchange rate and CEST concentration. Next, a semisolid pool, with a Lorentzian lineshape, symmetric about 0 ppm1,2, was added, and all three-pools were fit to determine how the model would react under more complex conditions. Lastly, another CEST pool at 3.5 ppm, with an exchange rate of 50 Hz (similar to that of amides), a CEST pool at 1.2 ppm, with an exchange rate of 1000 Hz (simulating hydroxyls), and two NOE pools at -2.25 and -3.25 ppm were added, for a total of seven pools, to determine how the model would react under more realistic conditions (see Table 1 for pool parameters). This seven-pool model was then fit using only a four-pool model (water, solute, confound at 3.5 ppm, and the semisolid pool) in order to evaluate the ability of the model to fit the solute of interest in the presence of multiple “unknown” confounds. Figure 1a-c displays the ideal simulated Z-spectra for the two-pool, three-pool, and seven-pool models, respectively, for the 50 Hz and 2000 Hz cases.
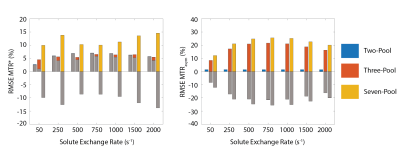
The results of these data were used to generate the MTR*, a measure of the MTRasym in an ideal two-pool model, as described in Chappell et al1, for each trial. The MTRasym was also calculated from the simulated data for comparison. The root-mean-square error (RMSE) against the true values was calculated for MTRasym and MTR*. These results were then plotted, along with the mean error, which was used as a measure of the bias in the estimates seen across the 100 instances.
Results
Figure 2 displays the RMSE and mean error for the MTR* and MTRasym over the 100 noise instances of the simulations. The RMSE of MTR* stays relatively constant across all exchange rates, and stays below 10% for the two- and three-pool models. Whilst the seven-pool model produces larger error, this is expected as the fitting parameters are not accounting for the complexity of the simulated data. Furthermore, the mean error of the MTR* is positive for the two- and three-pool models (indicating an overestimation of the MTR*), whereas the seven-pool model MTR* is underestimated. This result demonstrates that the model may over-fit the data if any confounding pools are present. Finally, the lower RMSE in the MTR* compared to the MTRasym for the three- and seven-pool data demonstrates that the MTRasym measure is not an appropriate parameter for measuring CEST effects from fast-exchanging species in normal biological systems.Conclusions
This study has shown that BayCEST accurately characterizes the CEST effect originating from fast-exchanging protons up to 2000 Hz, and outperforms MTRasym in the presence of confounding proton populations. Future work includes applying BayCEST to investigate fast-exchanging species in vivo, as well as comparing it with other analysis methods such as AREX3-5.Acknowledgements
Funding provided by: Whitaker International Program Fellowship and St. Hilda’s College Junior Research Fellowship.References
1. Chappell, M.A., et al. Quantitative Bayesian model-based analysis of amide proton transfer MRI. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine 70, 556-567 (2013).
2. Jones, C.K., et al. In vivo three-dimensional whole-brain pulsed steady-state chemical exchange saturation transfer at 7 T. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine 67, 1579-1589 (2012).
3. Zhang, X.Y., et al. CEST imaging of fast exchanging amine pools with corrections for competing effects at 9.4 T. NMR in biomedicine (2017).
4. Zaiss, M., et al. Relaxation-compensated CEST-MRI of the human brain at 7T: Unbiased insight into NOE and amide signal changes in human glioblastoma. NeuroImage 112, 180-188 (2015).
5. Ray, K.J., et al. Determination of an optimally sensitive and specific chemical exchange saturation transfer MRI quantification metric in relevant biological phantoms. NMR in biomedicine 29, 1624-1633 (2016).
Figures