2206
An automatically referenced quantitative susceptibility mapping algorithm: QSMauto_ref1Department of Electrical and Computer Engineering, Seoul National University, Seoul, Republic of Korea, 2Department of Radiology, Seoul St. Mary’s Hospital, College of Medicine, The Catholic University of Korea, Seoul, Republic of Korea, 3Division of Biomedical Engineering, Hankuk University of Foreign Studies, Yongin, Republic of Korea, 4Seoul National University, Seoul, Republic of Korea
Synopsis
We proposed a new QSM algorithm that automatically sets CSF as a susceptibility reference. The algorithm utilizes susceptibility effects on R2’ as a regularization term. The proposed algorithm does not require either segmentation of CSF or a well-refined brain mask and, therefore, can be used reliably.
Purpose
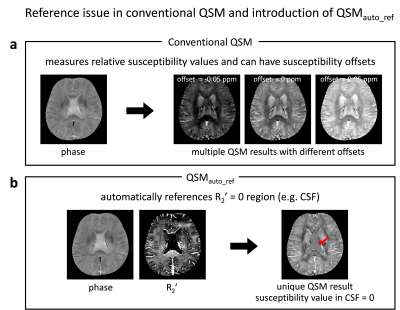
In quantitative susceptibility mapping (QSM), defining a proper reference has been one of the important challenges. So far, reference susceptibility has been set to the average susceptibility value of the whole brain or that of CSF1. The results of these approaches may depend on the brain mask or segmentation result2. In this study, we demonstrated a QSM algorithm that automatically enforces R2’ = 0 regions (e.g. CSF) as a susceptiblity reference (Fig. 1).Methods
[QSMauto_ref: Automatically referenced QSM] A susceptibility source in the magnetic field creates field perturbation that increases reversible transverse magnetization relaxation rate (R2’). This effect has been modeled as follows: $$R_2^{\:'}=D_m\:\cdot\:\sum |\chi|\:\:\:\:[Eq. 1] $$ where Dm is the effect size of unit susceptibility on R2’ (98 Hz/ppm3,4) and χ is the susceptibility value of each source in a voxel. When R2’ of a voxel is zero, susceptibility value should be bounded to zero according to the model.
In order to designate susceptibility reference regions as voxels with zero R2’, QSMauto_ref utilizes the following model: $$argim_{\chi_{pos},\chi_{neg}}|(R_2^{\:'}+i2{\pi}f)-D_m*(|\chi_{pos}+|\chi_{neg}|)-i2{\pi}D_p*(\chi_{pos}+\chi_{neg})|+{\lambda}g(\chi_{pos},\:\chi_{neg})\:\:\:\:[Eq. 2] $$ where f is frequency shift, Dp is a field perturbation kernel, g(χ) is a regularization term5, and λ is a regularization factor. The algorithm with no regularization and that with regularization were tested.
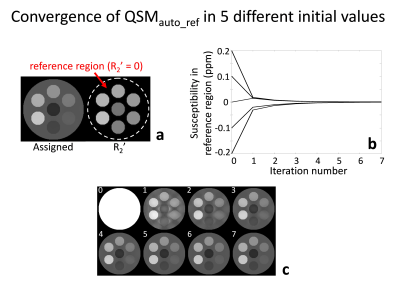
[Numerical simulation] A geometric phantom was deveoped to validate the proposed QSM algorithm. Total seven different cylinders were included in one large cylinder with different compositions of susceptibility values (values: -0.05:0.03:0.13, and 0 ppm; location: center, bottom, counter-clockwise, and large cylinder) and R2’ (values: 9:1:15, and 0 Hz; the same location as susceptibitlies). Frequency shift maps were generated following the dipole field convolution model6. In order to confirm the automatic convergence of the reference, five different initial susceptibility values were tested (Fig. 2b).
[In-vivo experiment] Five healthy volunteers were scanned at 3T MRI.
To estimate R2* and frequency shift, 3D multi-echo GRE data were acquired with the following parameters: voxel size=1×1×2mm3, TR=64ms, TE=2.9 to 25.9ms with echo spacing of 4.6ms, flip angle=22°, and acquisition time=7:02min. For R2* mapping, the multi-echo magnitude data were fitted to a mono-exponential decay function.
For R2 estimation, 2D multi-echo SE data were acquired with the following parameters: voxel size=1×1mm2, slice thickness=2mm, #slices=36, TR=4800ms, TE=20 to 120ms, and acquisition time=7:09min. R2 values were fitted from the multi-echo data with stimulated echo and slice-profile corrected mono-exponential fitting7.
Negative values of R2’ was set to zero enforcing physical mechanism. For an ROI analysis, six regions (see Fig. 4) were manually selected.
Results
In numerical simulation, the area with R2’ = 0 is indicated by red arrow in Fig. 2a. When five different initial susceptibility values were tested, all of the reconstructed susceptibility values in the R2’ = 0 region automatically converged to zero as the algorithm iterated (Fig. 2b). An example is visualized in Fig. 2c, revealing the automatic convergence of the susceptibility map from an initial point to the final results while enforcing the susceptibility reference to the region with R2’ = 0 (Fig. 2c).
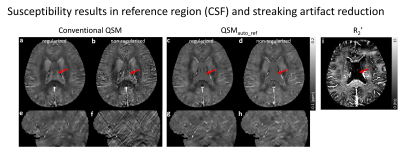
In the brain, the CSF region has nearly zero R2’ (red arrow in Fig. 3i). Therefore, the results from QSMauto_ref show uniformly zero susceptibilities in the CSF region (red arrows in Fig. 3c, d) while those from the conventional QSM reveal brighter and non-uniform contrasts (red arrows in Fig. 3a, b). QSM results, streaking artifacts become severe when regularization is not used (Fig. 3e, f). On the other hand, the new algorithm helps to prevent streaking artifacts. In the sagittal view of the conventional QSM results, streaking artifacts become severe when regularization is not used (Fig. 3e, f). On the other hand, there are no clear streaking artifacts in the non-regularized results of the proposed method (Fig. 3f, h).
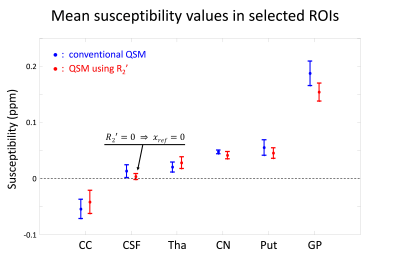
For further analysis, ROI averaged susceptibility values were reported (Fig. 4). In the CSF region, QSMauto_ref shows nearly zero susceptibility while the conventional QSM has positive susceptibility. This may result in the higher susceptibility values in deep gray matter (CN, Put, and GP) from the conventional QSM than those from the proposed algorithm.
Conclusion and Discussion
QSMauto_ref automatically enforces CSF as susceptibility reference in the brain. This approach requires no segmentation step and seems to be less sensitive to QSM mask enabling reliable QSM data analysis. Additionally, the proposed method shows robustness against streaking artifact. On the other hand, the linear R2’ model needs further investigated for regions with large source concentration (e.g. GP) or myelin microstructure (e.g. CC).Acknowledgements
This work was supported by Creative-Pioneering Researchers Program through Seoul National University(SNU) and by the Brain Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Science, ICT & Future Planning (NRF-2015M3C7A1031969).References
[1] Liu, Z., Spincemaille, P., Yao, Y., Zhang, Y., & Wang, Y. (2017). MEDI+0: Morphology enabled dipole inversion with automatic uniform cerebrospinal fluid zero reference for quantitative susceptibility mapping. Magnetic Resonance in Medicine.
[2] Bilgic, B., Pfefferbaum, A., Rohlfing, T., Sullivan, E. V., & Adalsteinsson, E. (2012). MRI estimates of brain iron concentration in normal aging using quantitative susceptibility mapping. Neuroimage, 59(3), 2625-2635.
[3] Langkammer, C., Schweser, F., Krebs, N., Deistung, A., Goessler, W., Scheurer, E., ... & Ropele, S. (2012). Quantitative susceptibility mapping (QSM) as a means to measure brain iron? A post mortem validation study. Neuroimage, 62(3), 1593-1599.
[4] Sedlacik, J., Boelmans, K., Löbel, U., Holst, B., Siemonsen, S., & Fiehler, J. (2014). Reversible, irreversible and effective transverse relaxation rates in normal aging brain at 3T. Neuroimage, 84, 1032-1041.
[5] Liu, T., Liu, J., De Rochefort, L., Spincemaille, P., Khalidov, I., Ledoux, J. R., & Wang, Y. (2011). Morphology enabled dipole inversion (MEDI) from a single‐angle acquisition: comparison with COSMOS in human brain imaging. Magnetic resonance in medicine, 66(3), 777-783.
[6] Salomir, R., de Senneville, B. D., & Moonen, C. T. (2003). A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering, 19(1), 26-34.
[7] McPhee, K. C., & Wilman, A. H. (2017). Transverse relaxation and flip angle mapping: evaluation of simultaneous and independent methods using multiple spin echoes. Magnetic resonance in medicine, 77(5), 2057-2065.
Figures