2204
Background Field Removal for Large Susceptibility Anatomical Structures in Human Brain with Orientation Variations1Department of Electronic Science, Xiamen University, Xiamen, China
Synopsis
We propose a novel background field removal method for large susceptibility anatomical structures, e.g., tissues around paranasal sinuses and interfaces of the tissue and skull, under various scanning orientations. The proposed method employs the gradient and magnitude of the phase map, combined with a normalized wrap count. Experimental results were both validated on four-orientation numerical simulation and in vivo human brain, which demonstrated the proposed method suppressed the residual phase error better than the other methods.
Introduction
The field perturbations are associated with geometric structure of the brain tissue, which indicates that the background field produced by the paranasal sinuses will contaminate the surrounding tissues as we change the head position during the scanning1,2. Published background field removal methods have to discard the brain tissues around these regions with a binary mask or remain different levels of residual phase errors 3. We propose an iRSHARP method that can effectively remove the orientation-dependent background field and suppress the susceptibility artifacts.Methods
Background field removal in the regions of large susceptibility can be removed using region adaptive spherical Gaussian kernels (SGK) depending on the local phase4. Then the local field $$$ B_{int}(r) $$$ is estimated from $$$ B_{int}(r)=(\delta - \rho_{G})\otimes^{-1}B_{temp}^\triangle $$$ where $$$ B_{temp}^\triangle $$$ is the interim dataset. The wrap count K(r) is calculated from the wrapped and unwrapped phase at the same echo that results from the evolution of total field perturbations at the echo time3,5. Accordingly, we assume that the standard deviation σ(r) of SGK can be formulated as $$$\sigma(r)=1/[M\cdot K(r)^{2}] $$$ where M is a positive constant. As we know, the background field in the large susceptibility regions is several orders of magnitude greater than the local field so that we can make an approximation that the background field equals to the total field. Since the background field $$$ B_{ext}(r) $$$ is harmonic through the entire volume of interest, a three-dimensional Taylor expansion is used to formulate the background field centering at r0 within a neighborhood (r0-R, r0+R) where R is the radius. Hence, the standard deviation σ(r) is related to the gradient ($$$\triangledown B^{\triangle}$$$) and magnitude ( $$$B^{\triangle}$$$) of the field map and a normalized term of wrap count $$$K_{n}\in[0,1]$$$, represented as $$$ \sigma(r)=1/[M\cdot (\triangledown B^{\triangle}+\epsilon)\cdot( B^{\triangle}+\epsilon)\cdot (K_n^2+\epsilon)] $$$ where $$$ \epsilon $$$ is a small positive constant to avoid dividing by zeros. The Gaussian kernel is $$$ \rho_{G}(m,n,l)=exp[-(m^{2}+n^{2}+l^{2})/2\sigma^{2}]/(\sigma\sqrt{2\pi}) $$$ with (m, n, l) denoting the point coordinate in SGK.Results
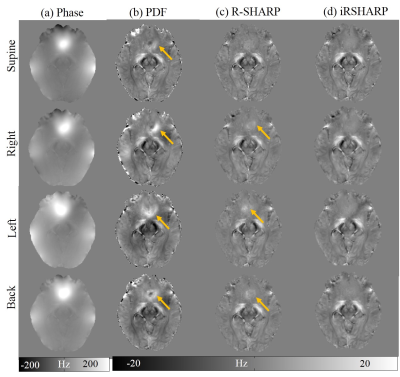
The numerical simulation data was created in a 128x128x64 matrix, in which five small spheroids were embedded to mimic the human brain tissues. The ball corresponding to paranasal sinus was rotated to simulate different head positions and a normal Gaussian noise was added to each head position data. In Fig. 1, the iRSHARP method shows better results than PDF, similar as R-SHARP but less computation time.
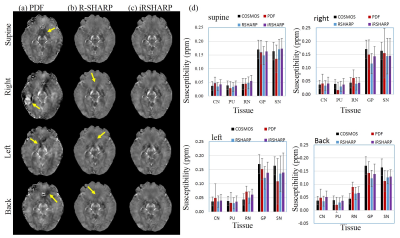
The in vivo human brain data was acquired from a healthy male volunteer on a 7T MRI scanner in Hospital of Johns Hopkins University approved by the local IRB. In Fig. 2, there are noticeable phase differences related to the head position around the paranasal sinuses. The PDF method cannot effectively remove the background field in these regions, while the R-SHARP method performs well at the supine position but tiny residual errors still can be observed at the other head positions. The proposed iRSHARP method performs best at all positions without noticeable residual errors. Susceptibility maps are reconstructed by SFCR method3 and COSMOS method is employed as the gold standard6. In Fig. 3, the susceptibility artifacts are well suppressed by the iRSHARP method which obtains more accurate susceptibility values of the deep gray nuclei as well.
Discussion
The iRSHARP method exploits a region adaptive spherical Gaussian kernel based on the spatial features of the dipole field, i.e. gradient and magnitude of field map and a normalized wrap count. These spatial features enable to detect the large susceptibility regions and adjust the Gaussian kernels adaptively. Experimental results on both multi-orientation numerical simulation and in vivo human brain data demonstrated that the proposed iRSHARP method can well suppress the background field and result in better susceptibility estimation at multiple head positions.Conclusion
Our proposed iRSHARP method can remove the orientation-dependent background field and outperforms the other methods. Compared to R-SHARP method, iRSHARP takes less computation time and is more convenient to use with less parameters, which can be applied in the related researches of quantitative susceptibility mapping and clinical diagnosis.Acknowledgements
This work was supported in part by NNSF of China under Grant 813012277, 113755147, Doctoral Program of Higher Education of China 20130121120010 and NSF of Fujian Province of Chine 2014J05099.References
[1] X. Li, D. S. Vikram, I. A. Lim, C. K. Jones, J. A. Farrell, and P. C. van Zijl, Mapping magnetic susceptibility anisotropies of white matter in vivo in the human brain at 7 T, Neuroimage, 2012; 62:314-330.
[2] L. Bao, X. Li, C. Cai, Z. Chen, P. van Zijl, Quantitative Susceptibility Mapping using Structural Feature based Collaborative Reconstruction (SFCR) in the Human Brain, IEEE transactions on medical imaging, 2016; 35(9):2040-2050.
[3] F. Schweser, A. Deistung, B. W. Lehr, and J. R. Reichenbach, Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: an approach to in vivo brain iron metabolism?, Neuroimage, 2011; 54:2789-2807.
[4] J. Fang, L. Bao, X. Li, P. C. M. V. Zijl, and Z. Chen, Background Field Removal Using A Region Adaptive Kernel for Quantitative Susceptibility Mapping of Human Brain, Journal of Magnetic Resonance, 2017; 281:130-140.
[5] M. A. Schofield, and Y. Zhu, Fast phase unwrapping algorithm for interferometric applications, Optics Letters, 2003; 28:1194-1196.
[6] Liu T, Spincemaille P, De R L, et al. Calculation of susceptibility through multiple orientation sampling (COSMOS): A method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI[J]. Magnetic Resonance in Medicine, 2009; 61(1):196–204.
Figures