2203

Nonlinear projection onto dipole fields with preconditioning (nPDF)
Carlos Milovic1,2, Berkin Bilgic3, Bo Zhao3, Christian Langkammer4, Julio Acosta-Cabronero5, and Cristian Tejos1,2

1Department of Electrical Engineering, Pontificia Universidad Catolica de Chile, Santiago, Chile, 2Biomedical Imaging Center, Pontificia Universidad Catolica de Chile, Santiago, Chile, 3Martinos Center for Biomedical Imaging, Harvard Medical School, Charlestown, MA, United States, 4Department of Neurology, Medical University of Graz, Graz, Austria, 5Wellcome Centre for Human Neuroimaging, UCL Institute of Neurology, University College London, London, United Kingdom

Synopsis

QSM requires to remove fields originated outside a region of interest prior to inversion. This is prone to generating artifacts due to noise and error propagation from previous processing steps such as coil combination or phase unwrapping. To address this, we reformulated the widely used projection onto dipole fields (PDF) method as a nonlinear problem with pre-conditioning. This new formalism is wrap-insensitive, results in improved noise/error management, and might enable a more straightforward implementation of multi-coil/-echo combination and background removal steps into a single optimizer.

PURPOSE

Quantitative susceptibility mapping (QSM) is inferred from nonlocal gradient-recalled echo (GRE) signals. Thus, most inversion algorithms require phase filtering procedures to exclude spurious background phase components originated outside of a predefined ROI. This is commonly achieved assuming that external sources generate harmonic fields inside the ROI1,2. For example, Laplacian-based3,4 approaches solve a Poisson equation with predefined boundary conditions. Other previously proposed methods exploit the spherical mean value property of harmonics5,6. Such approaches, however, have important caveats, e.g. the latter erodes the ROI to a smaller trustable region and the former is incompatible with fast Fourier algorithms, preventing it from an integration into single-step formulations. An alternative is to use the orthogonal property of the basis functions by iteratively modulating the strength of dipole sources outside the ROI (one per voxel). Dipoles outside the ROI generate harmonics inside, which through a least-squares minimization with respect to the measured field estimate the background field – this method is known as projection onto dipole fields (PDF)7. A common limitation of the aforementioned approaches is the requirement that the measured field must be accurately unwrapped. Wrapping errors generate artifacts potentially amplified and propagated in subsequent processing steps leading, thus, to incorrect susceptibility estimates. In order to extend PDF to operate directly on wrapped data, and theoretically improve noise propagation, we present the following preconditioned nonlinear PDF method:

METHODS

Given the nonlinear functional: $$$argmin_{\chi}\frac{1}{2}\parallel w(e^{id\star m\chi}-e^{i\phi})\parallel^2_2$$$ with d the dipole kernel, χ the susceptibility distribution, w a magnitude dependent weight, m an inverted ROI binary mask and ϕ the acquired phase. In the context of the alternating direction method of multipliers (ADMM)8,9, we first perform variable splitting by introducing an auxiliary variable $$$z=DF\chi$$$ to decouple the equation system into different subproblems and iterate between solutions until convergence. The subproblem for χ becomes: $$$argmin_{\chi} \frac{\mu}{2}\parallel F^HDFm\chi-z+s\parallel^2_2$$$, where s is the associated Lagrangian multiplier and μ is a Lagrangian weight. We introduce the variable $$$ z_2 = m\chi $$$ to further decouple the problem leading to: $$$argmin_{\chi,z_2}\frac{\mu}{2}\parallel F^HDFz_2-z+s\parallel^2_2+\frac{\mu_2}{2}\parallel m\chi-z_2+s_2\parallel^2_2$$$, which has closed-form solutions: $$$\chi=m(z_2-s_2)$$$ and $$$Fz_2=\frac{\mu D^HF(z-s)+\mu_2F(m\chi+s_2)}{\mu D^HD+\mu_2}$$$. Finally, the nonlinear subproblem z can be solved iteratively as in Milovic, et al10 with an initial estimate of the unwrapped phase consisting of an ROI-specific least-squares fitting procedure that solves for the step function, $$$\kappa d\star m+\phi_0$$$, with κ and ϕ0 constants. Thus, the nonlinear PDF operation can be seen as a perturbation from such preconditioned initial state.

The proposed algorithm—empirically set to converge for 1,500 iterations with μ=0.0018—was compared with original PDF and Laplacian boundary value (LBV) methods—both initialized with Laplacian and iterative-Laplacian unwrapped phases11 in the following experiments:

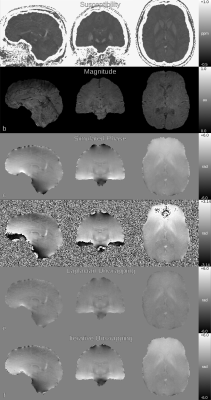
A) COSMOS12 ground-truth (3D spoiled-GRE on a 3T Siemens Tim Trio with 1.06-mm isotropic voxels, 240×196×120, TE/TR=25/35ms, 12 head orientations), from which a noisy field map was forward simulated with a widespread distribution of external sources (Fig. 1).

B) In vivo data (3D spoiled-GRE on a 3T Philips system, 352×352×170, 0.6×0.6×1.0 mm3, TE/TR=[7.2,13.4,19.6,25.8,32]/44ms, α=17°) processed with an in-house temporal unwrapping algorithm and subsequent magnitude-weighted nonlinear multi-echo combination.

QSM was calculated from all pre-filtered field maps using the FANSI toolbox10 with μ2 set to 1.0.

RESULTS

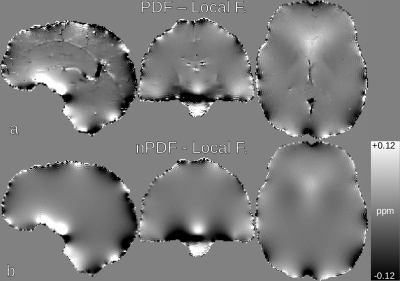
A) Resulting field maps, RMSE scores and difference maps are shown in Fig. 2. nPDF returned the lowest RMSE values and a less structured residual than the original PDF method (Fig. 3). RMSE scores for QSM (not shown) relative to COSMOS were: LVB=70.3%, PDF=61.5% and nPDF=58.6%, respectively. A stability test on the ADMM μ parameter revealed less than 0.5% RMSE variation for a μ range spanning an order of magnitude.

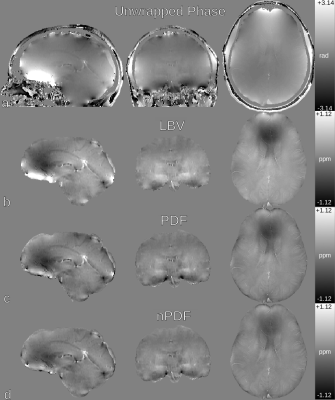
B) Fig. 4 illustrates the resulting local field estimates from the three background filtering algorithms investigated in the present study. Qualitatively, although all methods incompletely removed the background field, nPDF yielded the least prominent residual from dipole fields originated from cranial cavities.

DISCUSSION & CONCLUSION

The present study demonstrates accurate preconditioning is crucial for robust nonlinear PDF. Provided this is achieved, the proposed method results in improved noise management, less vulnerability to error propagation and overall, improved robustness to inaccuracies near the ROI boundary, which is highly desirable as it enables minimal or no erosion to the trustable region. Since this algorithm works with raw data as input, it may be extended to perform simultaneous coil or multi-echo combinations.

Acknowledgements

FONDECYT 1161448, CONICYT Programa PIA Anillo ACT1416, Becas de Doctorado Nacional CONICYT Folio 21150369 and Wellcome-UK [203147/Z/16/Z].

References

1. Li L, Leigh JS. Quantifying arbitrary magnetic susceptibility distributions with MR. Magn. Reson. Med. 2004; 51: 1077–1082.

2. Li L, Leigh JS. High-precision mapping of the magnetic field utilizing the harmonic function mean value property. J. Magn. Reson. 2001; 148: 442–448.

3. Zhou D, Liu T, Spincemaille P, Wang Y. Background field removal by solving the Laplacian boundary value problem. NMR in Biomedicine. 2014;27(3):312–319.

4. Li W, Avram AV, Wu B, Xiao X, Liu C. Integrated Laplacian-based phase unwrapping and background phase removal for quantitative susceptibility mapping. NMR Biomed. 2014;27(2):219-227.

5. Schweser F, Deistung A, Lehr BW, Reichenbach JR. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: an approach to in vivo brain iron metabolism? Neuroimage 2011;54:2789–2807.

6. Wu B, Li W, Guidon A, Liu C. Whole brain susceptibility mapping using compressed sensing. Magn Reson Med. 2012;67(1):137–147.

7. Liu T, Khalidov I, de Rochefort L, Spincemaille P, Liu J, Tsiouris AJ, Wang Y. A novel background field removal method for MRI using projection onto dipole fields (PDF) NMR Biomed. 2011;24(9):1129–1136.

8. Bilgic B, Chatnuntawech I, Langkammer C, Setsompop K. Sparse Methods for Quantitative Susceptibility Mapping. Wavelets and Sparsity XVI, SPIE 2015. doi: 10.1117/12.2188535

9. Zhao B, Setsompop K, Ye H, Cauley S. and Wald LL. Maximum likelihood reconstruction for magnetic resonance fingerprinting, IEEE Trans Med Imaging 2016;35:1812-1823.

10. Milovic C, Bilgic B, Zhao B, Acosta-Cabronero J, Tejos C. A Fast Algorithm for Nonlinear QSM Reconstruction with Variational Penalties. Proceedings of the Fourth International Workshop on MRI Phase Contrast & Quantitative Susceptibility Mapping. 2016;1:132.

11. Schofield MA, Zhu Y. Fast phase unwrapping algorithm for interferometric applications. Opt Lett. 2003;28(14):1194–1196.

12. Liu T, Spincemaille P, De Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): A method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magnetic Resonance in Medicine. 2009;61(1):196–204.

Figures

Fig. 1: COSMOS-brain experiment. a) Ground truth susceptibility, b) magnitude, c) forward simulated phase, d) Noise-corrupted, wrapped phase (i.e. input data), e) Laplacian unwrapping, f) Iterative-Laplacian unwrapping.

Fig. 2: Results for the COSMOS-brain experiment. a) Simulated, noise-corrupted local field. b), d), f), h) and j) are the local fields from all algorithms evaluated (in parenthesis the unwrapping method used as pre-processing). c), e), g), i) and k) are the corresponding difference maps. In the top right corners are displayed the RMSE scores for each reconstruction.

Fig. 3 Contrast-enhanced version of Fig. 2e and 2k, respectively.

In vivo local field results for all algorithms investigated. Input phase is the result of temporal unwrapping and subsequent nonlinear multi-echo combination.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
2203