2197

Machine Learning in QSM:   Inversion Using Multi-Resolution Decomposition and Convolutional Neural Networks.
Kevin Koch1, Tugan Muftuler2, Robin Karr1, and Andrew Nencka1

1Radiology, Medical College of Wisconsin, Wauwatosa, WI, United States, 2Medical College of Wisconsin, Wauwatosa, WI, United States

Synopsis

One of the remaining translational challenges in QSM is the need for post-processing algorithms that are rapid, robust, and accurate. Here, we present an alternative formulation of the QSM inversion problem. The field-to-source inversion is divided into a multi-resolution decomposition, whereby each resolution stage is divided into small independent processing regions. The basic premise of this concept is the isolate local susceptibility fields and sources at varying levels of resolution. When the susceptibility problem is divided in this fashion, field-to-source inversions can occur in regions of very volumetric matrix sizes (with varying voxel sizes per inversion). After inverting each of the sub-volumes, a combination procedure is implemented to combine the volumes and the resolution layers. Due to the small size of the inversion volumes, the dimensionality of the problem lends itself to the use of convolutional neural network modeling and application.

Introduction

One of the remaining translational challenges in QSM is the need for post-processing algorithms that are rapid, robust, and accurate. Multi-orientiation acquisition and processing techniques [1] are the most robust approaches to QSM, but are not viable in a clinical workflow. Many regularization techniques have been proposed to stabilize the inversion, though most of the techniques have a substantial tradeoff between accuracy, robustness, and processing time [2]. Here, we present an alternative formulation of the QSM inversion problem. The field-to-source inversion is divided into a multi-resolution decomposition, whereby each resolution stage is divided into small independent processing regions. The basic premise of this concept is the isolate local susceptibility fields and sources at varying levels of resolution. When the susceptibility problem is divided in this fashion, field-to-source inversions can occur in regions of very volumetric matrix sizes (with varying voxel sizes per inversion). After inverting each of the sub-volumes, a combination procedure is implemented to combine the volumes and the resolution layers. Rapid mechanisms must be used for each of the volume inversions. Due to the small size of the inversion volumes, the dimensionality of the problem lends itself to the use of convolutional neural network modeling and application. Here, we demonstrate the multi-resolution decomposition, inversion, and reconstruction concept. In addition, present a convolutional neural network that was successfully trained to invert 8x8x8 volumetric regions similar to those used in this multi-resolution decomposition demonstration.

Methods

The input tissue field and COSMOS inversion result of the 2016 ISMRM Workshop Challenge dataset was utilized for this demonstration [3]. A rudimentary multi-resolution decomposition was utilized for this demonstration. Twenty-eight resolution layers were constructed through successive blurring and residual propagation of the input maps. The matrix dimensions of each layer were reduced successively by subtractions of four in each dimension. Each layer was then sub-divided into 8x8x8 volumetric regions, which overlapped each other by 50%. Beginning with an interpolated isotropic 256x256,256 grid, this process resulted in over 200,000 8x8x8 regions to be inverted (within the tissue mask). For an initial demonstration, these regions were then inverted using a closed form L2 regularized approach [4]. The inverted volumes were then combined into composite layer maps at each resolution, and then the layer maps were simply added in a scaled superposition to form a final composite map. A 3D convolutional neural network was trained on real volumetric regions at the highest resolution layer. The training set consisted of 4500 regions with high variance relative to the norm of the full layer set. 500 regions were set aside for testing purposes. The network was constructed in TensorFlow using the Python API. 6 layers, using layer feature maps of [512, 256, 128, 64, 32, 1], isotropic 3D convolution kernels of [2 6 6 4 2 2], 330 epochs using batch sizes of 128 volumes. The dataset was allowed to train for 30 hours on a k80 GPU machine.

Results

Figure 1 presents several field maps at different resolution settings (top row), along with the residual fields (second row) computed through a forward model convolution using input susceptibilities (COSMOS) within the volumetric isolation scheme.

Figure 2 presents several susceptibility inputs at different resolution settings (top row), along with the inverted maps (second row) computed through the local closed form inversion within the volumetric isolation scheme.

Figure 3 provides maps in three different planes computed using the input tissue field and the iterative FANSI [5] technique, closed form L2 [3], and multi-resolution volumetric isolation approaches.

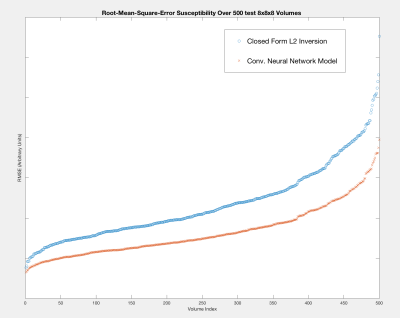
Figure 4 presents the results of the convolutional neural network performance on a selection of 500 volumes extracted from the highest resolution multi-resolution layer. Figure 5 presents the accuracy improvements feasible when using the neural network model in comparison to the L2 approach.

Discussion

In summary, we have outlined a process that allows for substantial dimensionality reduction of the QSM inversion process. This multi-resolution approach considers the importance of capturing distant field effects in the inversion process, while allowing for inversion of small low-matrix size volumes. This approach is very well suited to machine learning application using GPU computations of applied models. Here, we have demonstrated the training and accuracy improvements feasible with a convolutional neural network. The network was trained on real multi-resolution maps — at a worst case scenario in the highest resolution layer. Future work will investigate improved multi-resolution decomposition schemes, which move beyond the crude linear approach demonstrated in this example. In particular, wavelet resolution decomposition is expected to provide more advantageous decomposition capabilities.

Acknowledgements

No acknowledgement found.

References

[1] Liu et al, Calculation of susceptibility through multiple orientation sampling (COSMOS): a method for conditioning the inverse problem from measured magnet- ic field map to susceptibility source image in MRI. Magn Reson Med 2009

[2]Wang et al, Quantitative susceptibility mapping (QSM): Decoding MRI data for a tissue magnetic biomarker. Magnetic Resonance in Medicine, 2014

[3] Langkammer et al, Quantitative susceptibility mapping: Report from the 2016 reconstruction challenge, MRM, 2017

[4] Bilgic et al, Fast image reconstruction with L2 regularization, JMRI, 2014

[5] C. Milovic et al, A Fast Algorithm for Nonlinear QSM Reconstruction, ISMRM'17 p3669

Figures

Figure 1 presents several field maps at different resolution settings (top row), along with the residual fields (second row) computed through a forward model convolution using input susceptibilities (COSMOS) within the volumetric isolation scheme. The far left column of the second row shows the scaled combination of the computed field. The accuracy of the resolution decomposed images demonstrates the ability of the localized processing to accurately convolve the local field. The errors in the combined field are due to imperfect characterization of the multi-resolution decomposition applied in this demonstration. The far left column of the second row shows the scaled combination of the computed field.

Figure 2 presents several susceptibility inputs at different resolution settings (top row), along with the inverted maps (second row) computed through the local closed form inversion within the volumetric isolation scheme. These inversions utilized the multi-resolution inputs in the top row of Figure 1 at each isolation layer. The far left column of the second row shows the scaled combination of the computed susceptibility map. Similar to Figure 1, the results show excellent accuracy within the individual layers, but a slightly compromised composite combination — again, due to the crude multi-resolution decomposition.

Figure 3 provides maps in three different planes computed using the input tissue field and the iterative FANSI [5] technique, closed form L2 [3], and multi-resolution volumetric isolation approaches. Of note, the streaking reduction and resolution feasible with the multi-resolution approach are advantageous compared to the other two methods. The L2 approach shows substantial streaking across the entire brain, but shows no visible streaking when applied within the local volumes in the multi-resolution approach.

Figure 4 presents the results of the convolutional neural network performance on a selection of 500 volumes extracted from the highest resolution multi-resolution layer. The applied network is shown in two slices of one volume and compared to the input susceptibility (gold standard) and the L2 approach used for the aforementioned multi-resolution demonstration.

Figure 5 presents the accuracy improvements feasible when using the neural network model in comparison to the L2 approach.Both approaches can be applied very quickly, and are well suited for GPU application. However, it is clear that the neural network outperforms the L2 closed form, particularly in the cases of more severe susceptibility variations prone to greater inversion error.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
2197