2194
Phase Corrected Bipolar Acquisition for Simultaneous Water-Fat Separation and Quantitative Susceptibility Mapping of the Carotid Artery Wall1Department of Radiology, University of Cambridge, Cambridge, United Kingdom, 2Department of Radiology, Cambridge University Hospitals NHS Foundation Trust, Cambridge, United Kingdom
Synopsis
In this work we investigated the feasibility and assessed the performance of a bipolar compared to a unipolar gradient echo readout for a combined method of water-fat separation and quantitative susceptibility mapping for application in the carotid artery wall.
Introduction
Carotid atherosclerosis involves formation of plaques, which may rupture and cause ischemic stroke.1 Plaques can become calcified and may contain haemorrhage1, which makes them of interest for investigation using Quantitative Susceptibility Mapping (QSM). Application in the neck requires modification of the processing, to avoid errors in the field non-uniformity map ΔB, caused by the water-fat chemical shift, which propagate into susceptibility maps. We have previously implemented the IDEAL water-fat separation to correct for these errors when performing QSM in the neck.2,3,4
IDEAL fits complex multi-echo gradient echo MR data to estimate water, fat, and ΔB. Increasing the number of echoes and shortening echo spacing have shown to improve SNR and reduce phase wraps in QSM,5 and to improve robustness of IDEAL processing.6 Using bipolar instead of unipolar readout gradients, improves acquisition efficiency while minimizing echo spacing. However, opposite readout gradient polarities cause phase discrepancies between odd and even echoes, that require compensation. We investigated the feasibility and potential benefits of acquiring data with bipolar sequences for simultaneous water-fat separation and QSM in the neck compared to the conventional unipolar echoes.
Methods
The phase φ of the multi-echo gradient echo sequence is a function of ΔB, echo time TE, initial phase offset φ0, and the gradient polarity specific phase offsets Δθi(x,y), which are caused by gradient delays and eddy currents:
φ(x,y,TEEVEN)=φ0-γΔB(x,y)TEEVEN+Δθ1(x,y)
φ(x,y,TEODD)= φ0-γΔB(x,y)TEODD+Δθ2(x,y)
We subsequently implemented a correction to remove these offsets.7-11 A nonlinear fit of the complex data from odd echoes gives the phase difference Φ=-γΔB(x,y)(TE3-TE1).12-14 After spatial phase unwrapping15 and scaling by a factor of TEi/(TE3-TE1), Φ corresponds to the phase at TEi without any offset. The differences between Φ and the phase of the complex images S at echo times TE1 and TE2 give the gradient polarity specific offsets:
Δθ1(x,y)+φ0=∠(S(TE1)conj(ei*Φ*TE1/(TE3-TE1)))
Δθ2(x,y)+φ0=∠(S(TE2)conj(ei*Φ*TE2/(TE3-TE1)))
We assumed that the phase offset varies linearly in space7-10 and can be described by two constants, m and n, and is modeled as Δθi(x,y)fitted=mx+ny+b. This was used to correct the complex data so that even and odd echoes are without phase offset(Fig.1):
S(TEODD)corr= S(TEODD)conj(eiΔθ1(x,y)fitted)
S(TEEVEN)corr= S(TEEVEN)conj(ejΔθ2(x,y)fitted)
Six healthy subjects were scanned using a 3D multi-echo gradient echo acquisition with bipolar gradients at 3T (MR 750, GE Healthcare, Waukesha, WI) and one patient with carotid artery stenosis at 1.5T (MR450w, GE Healthcare, Waukesha, WI)(Table1). Before performing QSM, the phase offsets from odd and even echoes were removed from the bipolar dataset. This is unnecessary when using odd echoes only, since they all have the same offset Δθ1(x,y). The results from both datasets were compared using a large number of echoes (twelve bipolar/six unipolar), to assess feasibility of using bipolar acquisitions for QSM and IDEAL, and a smaller number (eight/four) to assess potential improvements of bipolar acquisitions if the results of the unipolar echoes are degraded. QSM consisted of estimating ΔB using IDEAL,2,3 followed by background field removal16-18 and dipole field inversion to estimate the susceptibility map.19-23
Results
The unipolar and bipolar methods produced similar results, using six and twelve echoes respectively(Fig.2). Water-fat separation robustly estimated ΔB with minimal artifacts which resulted in clear visualization of anatomical features like fat and vessel wall on both susceptibility maps. The measured susceptibility difference between tissue and fat, 0.57ppm, agreed with previously published values, 0.61ppm.3,26
When limiting the number of unipolar echoes to four, ΔB showed errors at the boundary between water and fat that resulted in streaking artifacts on the susceptibility map(Fig.3.a),c)). The use of all eight bipolar echoes acquired during the same time improved image quality on ΔB and removed streaking artifacts(Fig.3.b),d)) to allow for clear visualization of relevant anatomical features.
In the patient scan a bipolar acquisition produced susceptibility maps in which the vessel wall and a strongly diamagnetic region (thought to be vessel wall calcification) were clearly identifiable(Fig.4).
Discussion
The feasibility of performing simultaneous water-fat separation and QSM using bipolar echo readouts was demonstrated in comparison with the unipolar method using a large number of echoes. Reducing the number of echoes degraded ΔB estimation. Strong errors on ΔB from the unipolar acquisition caused severe streaking artifacts on the susceptibility maps that could be minimized using additional bipolar echoes. In the patient scan the number of echoes was limited to six since minimum echo spacing was increased in the wide bore MRI scanner. Therefore, we used a bipolar acquisition which produced high quality susceptibility maps.Conclusion
In this work we were able to demonstrate the feasibility of using bipolar readout gradients for simultaneous water-fat separation and QSM and its potential in increasing robustness of estimating ΔB, when limited echo data is available.Acknowledgements
Pascal Ruetten is funded by a Medical Research Council/Sackler Stipend.References
[1] Gillard, Jonathan, et al., eds. "Carotid disease: the role of imaging in diagnosis and management." Cambridge University Press, 2006.
[2] Reeder, Scott B., et al. "Multicoil Dixon chemical species separation with an iterative least‐squares estimation method." Magnetic Resonance in Medicine 51.1 (2004): 35-45.
[3] Dimov, Alexey V., et al. "Joint estimation of chemical shift and quantitative susceptibility mapping (chemical QSM)." Magnetic resonance in medicine 73.6 (2015): 2100-2110.
[4] Ruetten, Pascal P R, et al. "Quantitative Susceptibility Mapping of the Carotid Artery Wall using IDEAL" 34th Annual Scientific Meeting of ESMRMB; Barcelona. 2017; abstract 798
[5] Haacke, E. Mark, et al. "Quantitative susceptibility mapping: current status and future directions." Magnetic resonance imaging 33.1 (2015): 1-25.
[6] Yu, H.; Shimakawa, A.; McKenzie, CA.; Vu, AT.; Brau, ACS.; Beatty, PJ.; Reeder, SB.; Brittain, JH. "A multi-echo acquisition method with reduced echo spacing for robust IDEAL water-fat decomposition at 3T." Proceedings of the 16th Scientific Meeting of ISMRM; Berlin. 2007. abstract 3353
[7] Feng, Wei, Jaladhar Neelavalli, and E. Mark Haacke. "Catalytic multiecho phase unwrapping scheme (CAMPUS) in multiecho gradient echo imaging: removing phase wraps on a voxel‐by‐voxel basis." Magnetic resonance in medicine 70.1 (2013): 117-126.
[8] Li, Jianqi, et al. "Phase-corrected bipolar gradients in multi-echo gradient-echo sequences for quantitative susceptibility mapping." Magnetic Resonance Materials in Physics, Biology and Medicine28.4 (2015): 347-355.
[9] Yu, Huanzhou, et al. "Phase and amplitude correction for multi‐echo water–fat separation with bipolar acquisitions." Journal of Magnetic Resonance Imaging 31.5 (2010): 1264-1271.
[10] Lu, Wenmiao, et al. "Water–fat separation with bipolar multiecho sequences." Magnetic resonance in medicine 60.1 (2008): 198-209.
[11] Sun, Hongfu, et al."Phase Correction of a Bipolar Gradient-Echo Acquisition for Quantitative Susceptibility Mapping" Proceedings of the 24th Scientific Meeting of ISMRM; Singapore. 2016. abstract 2987
[12]Liu, Tian, et al. "Nonlinear formulation of the magnetic field to source relationship for robust quantitativesusceptibility mapping." Magnetic resonance in medicine 69.2 (2013): 467-476.
[13] Kressler, Bryan, et al. "Nonlinear regularization for per voxel estimation of magnetic susceptibility distributionsfrom MRI field maps." IEEE transactions on medical imaging 29.2 (2010): 273.
[14] de Rochefort, Ludovic, et al. "Quantitative MR susceptibility mapping using piece-wise constant regularizedinversion of the magnetic field." Magnetic Resonance in Medicine 60.4 (2008): 1003-1009.
[15] graph cut phase unwrapping, code available from "http://weill.cornell.edu/mri/pages/qsm.html"
[16] Zhou, Dong, et al. "Background field removal by solving the Laplacian boundary value problem." NMR inBiomedicine 27.3 (2014): 312-319.
[17] Liu, Tian, et al. "A novel background field removal method for MRI using projection onto dipole fields." NMR in Biomedicine 24.9 (2011): 1129-1136.
[18] de Rochefort, Ludovic, et al. "Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging." Magnetic Resonance in Medicine 63.1 (2010): 194-206.
[19] Liu, Tian, et al. "Nonlinear formulation of the magnetic field to source relationship for robust quantitativesusceptibility mapping." Magnetic resonance in medicine 69.2 (2013): 467-476.
[20] Liu, Jing, et al. "Morphology enabled dipole inversion for quantitative susceptibility mapping using structuralconsistency between the magnitude image and the susceptibility map." Neuroimage 59.3 (2012): 2560-2568.
[21] Liu, Tian, et al. "Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: comparison withCOSMOS in human brain imaging." Magnetic resonance in medicine 66.3 (2011): 777-783.
[22] de Rochefort, Ludovic, et al. "Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging." Magnetic Resonance in Medicine 63.1 (2010): 194-206.
[23] Shmueli, Karin, et al. "Magnetic susceptibility mapping of brain tissue in vivo using MRI phase data." Magnetic Resonance in Medicine 62.6 (2009): 1510-1522.
[24] the codes referenced in [12-22] are available at "http://weill.cornell.edu/mri/pages/qsm.html"
[25] code from [23] from "Wang, Yi, and Tian Liu. "Quantitative susceptibility mapping (QSM): decoding MRI datafor a tissue magnetic biomarker." Magnetic resonance in medicine 73.1 (2015): 82-101."; available at"http://weill.cornell.edu/mri/pages/qsmreview.html"
[26] Szczepaniak, Lidia S., et al. "Bulk magnetic susceptibility effects on the assessment of intra‐and extramyocellular lipids in vivo." Magnetic resonance in medicine 47.3 (2002): 607-610.
Figures
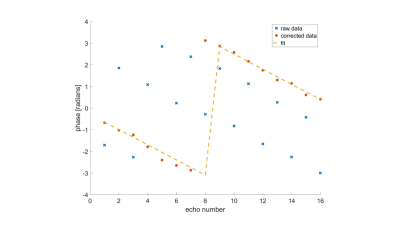

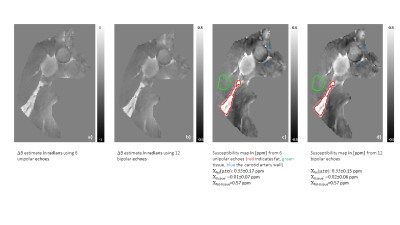
Figure 2: Feasibility of using bipolar echoes for QSM in the neck

Figure 3: Artifact reduction on susceptibility maps through the use of bipolar echoes
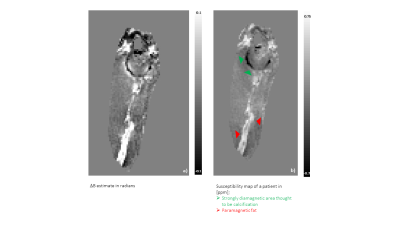
Figure 4: Application of the proposed bipolar data acquisition for QSM in a patient