2103
Improving susceptibility mapping using multiple thresholding k-space division19000 Rockville Pike, CNRM, NIH/USU, Bethesda, MD, United States, 2National Institutes of Health, Bethesda, MD, United States
Synopsis
A major challenge in QSM is inverting the acquired phase measurement to estimate the underlying susceptibility. Thresholded K-space division (TKD) is a straightforward technique to calculate the magnetic susceptibility distribution from a single orientation phase images. In this work, we propose to obtain an optimal inverse dipole kernel by using multiple thresholding to minimize the RMSE of the resultant susceptibility map against a susceptibility map
Introduction
Quantitative Susceptibility Mapping (QSM) is a quantitative method to measure magnetic susceptibility from the acquired phase. A major challenge in QSM is inverting the acquired phase measurement to estimate the underlying susceptibility. The inversion is ill-posed because it involves inverting zeros lying on the cone surface of the dipole kernel with polar angles of ±54.7° with respect to the B0 field. One way to overcome this issue is to acquire data from multiple orientations to overlay the zeros of one dipole kernel with non-zeros of other dipole kernels. However, acquiring data from multiple orientations is time intensive and impractical. Thresholded K-space division (TKD) is a straightforward technique to calculate the magnetic susceptibility distribution from a single orientation phase images [1,2]. In the TKD method, the inversion is performed by truncating the direct inversion of the dipole kernel by a constant value δ. The thresholded inverse dipole kernel Dinv is expressed as
Dinv(δ,k) = (1/3 - kz×kz/k2)-1 if |1/3 - kz×kz/k2|>δ,
= sign(1/3 - kz×kz/k2) x δ-1 otherwise.
The TKD method is easy to implement and is relatively fast. Its accuracy, however, is moderate. In the 2016 QSM reconstruction challenge3, a version of TKD (UCL TKD 1) was ranked 7th in the category of root mean squared error (RMSE). In this work, we propose to obtain an optimal inverse dipole kernel by using multiple thresholding to minimize the RMSE of the resultant susceptibility map against a reference susceptibility map obtained from multiple-orientation tissue phase images using either the susceptibility tensor imaging approach4.
Method
Tissue phase images, the brain mask, orientation vectors, and a susceptibility map (χ33), and a TKD script (δ = 0.19) were downloaded from 2016 QSM workshop website3. The χ33 map, which was reconstructed from tissue phase images of 12 orientations, served as the reference susceptibility map in this work.
We performed the optimization of the inverse dipole kernel by minimizing the RMSE value with respect to the reference map. The optimization steps used to generate the optimal inverse kernel (Dinv_opt) are described below:
(1) Initialize an inverse dipole kernel using Eq (1) with δ = 0.67,
(2) Iterate a range of threshold values for kz = 0, e.g. from 0.1 to 0.4 with an increment of 0.01,
(3) Select the threshold value that gives minimal RMSE, and update Dinv_opt at ±kz with the optimal threshold,
(4) Repeat steps 2-3 for each kz up to the periphery of k-space (max kz).
Results
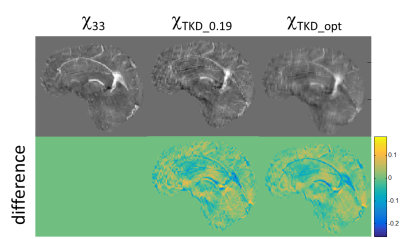
The axial and sagittal views of the optimized inverse dipole kernel (Dinv_opt) and the inverse dipole kernel with δ = 0.19 (Dinv_0.19) are shown in Figure 1. As compared to Dinv_0.19, the plot of the Dinv_opt kernel is relatively uniform because of larger threshold values. Furthermore, optimal threshold values of low frequencies (low kz) of Dinv_opt were smaller than those of mid and high frequencies. The susceptibility maps χTKD_0.19 and χTKD_opt reconstructed from Dinv_0.19 and Dinv_opt respectively were compared with the reference χ33 map, shown in axial and sagittal views in Figures 2 and 3 respectively. The proposed Dinv_opt in this work led to a RMSE of 72.7, which was better than the RMSE of 86.49 from χTKD_0.19.
Discussion and Conclusion
It is well know that the TKD method with a small threshold value will results in a susceptibility map with prominent streaking artifacts. These streaking artifacts comprise mostly high frequencies, and can be substantially reduced by using a threshold value in the range of 0.2 to 0.52. The QSM reconstructed using the proposed optimal inverse dipole kernel is blurry because the optimization is performed with respect to a blurry reference map. The RMSE from this multiple thresholding k-space division is small that it would be the 3rd best algorithm in the RMSE category in 2016 QSM challenge. Lastly, while the optimization is performed against a gold standard susceptibility map using RMSE as a criterion, the multiple thresholding k-space division can be used for optimization using other criteria.
Acknowledgements
This work was supported by the Intramural Program of the National Institutes of Health, and the Department of Defense in the Center for Neuroscience and Regenerative Medicine.References
[1] Warton et al., MRM 2010;63:1292-1304.
[2] Shnueli et al., MRM 2009;62:1510-1522.
[3] http://qsm.neuroimaging.at/.
[4] Liu, MRM 2010;63:1471-1477.
Figures

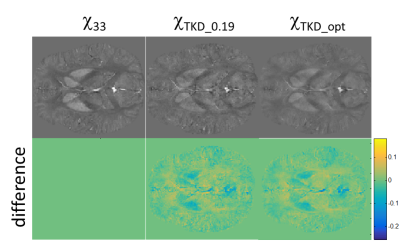
Comparison of χTKD_0.19 and χTKD_opt with the reference χ33. (upper row), as well as their differences (bottom row), in axial view.