2054
Eight fold acceleration for isotropic T2w and T2FLAIR imaging using Multi-Contrast Second-Order Directional Total Generalized Variation (dTGV).1Weill Cornell Medical College, New York, NY, United States, 2Cornell University, Ithaca, NY, United States
Synopsis
We propose a second-order directional total generalized variation (dTGV) that makes use of directional edge information in T1w to reconstruct highly undersampled T2w and T2FLAIR data. This allows a further doubling of the acquisition speed over the standard four fold accelerated protocol. The proposed dTGV regularizer promotes structural similarity between contrasts.
INTRODUCTION
In clinical MRI, multiple contrasts such as T1w, T2w, and T2 FLAIR are sequentially acquired one at a time. The lengthy scan time increases patient discomfort and decreases patient compliance. Although there has been abundant research in parallel imaging and compressed sensing to shorten scanning time, many techniques focus on acceleration a single scan. Anatomical images in different contrasts have structural information in common, which is exploited here to further accelerate multicontrast MRI data acquisition. To this end, we propose second-order directional total generalized variation (dTGV) that makes use of such structural information for a variational image reconstruction of highly undersampled MRI data.
THEORY
1) Rank-2 Orthogonal Projector
In this work, the structural information that coexists between contrasts is encoded using the orientation of edges (up to sign) of T1w. We extract this information using the following rank-2 orthogonal projector:
$$ \mathbb{M} = \left( \begin{array}{ccc} \mathbb{M}_{11} & \mathbb{M}_{12} \\ \mathbb{M}_{21} & \mathbb{M}_{22} \\ \end{array} \right) = I - \frac{(\nabla w)(\nabla w)^\top}{(\nabla w)^\top(\nabla w)},$$
where $$$w$$$ is the T1w image. That is, the operator $$$\mathbb{M}$$$ acts on a vector and extracts perpendicular component of the vector with respect to $$$\nabla w$$$. Fig. 1 shows this projector computed from a T1w image.
2) Direction Total Generalized Variation (dTGV) based Multicoil/Multicontrast MRI Reconstruction
The dTGV MRI reconstruction solves
$$ \min_{u,v} \frac{1}{2}\sum_{j=1}^{P}\|\Omega{\cal F}S_ju - g_j \|_2^2 + \alpha_1 \|\mathbb{M}\nabla u - v \|_1 + \alpha_0\|Ev\|_1,$$
where $$$g_1, \dots, g_P$$$ is the undersampled multichannel k-space raw data, P the number of channels, $$$S_1, \dots, S_P$$$ coil sensitivity maps, and $$$\Omega$$$ the k-space sampling mask. The last two terms are a variation of second-order TGV [2]. Observe that the rank-2 orthogonal projector is involved in the first L1 regularization term, which promotes parallel orientation of edges that coexist in T1w and T2w/T2 FLAIR. The operator is the symmetrized gradient. This optimization is then solved by the Chambolle—Pock algorithm with further dualization on the first term.
METHOD
Four healthy subjects were scanned at a 3T GE scanner with 32ch coils to acquire SAG 3D T1 BRAVO, SAG CUBE T2, and SAG CUBE T2 FLAIR with 1mm isotropic resolution and 1 healthy subject was scanned at the same system to acquire SAG 3D T1 BRAVO and SAG CUBE T2 with 1mm isotropic resolution. For T2w and T2 FLAIR, we acquired 1) fully sampled data, 2) standard data (ACC slice 2 x phase 2), 3) undersampled data (ACC slice 2 x phase 4). Matrix size is 256x256x192 and scan time was: 5:11 min for T1w, 34:46 min for fully sampled T2 FLAIR, 8:56 min for standard T2 FLAIR, 5:23 min for the proposed sampling scheme, 18:59 min for fully sampled T2w, 3:58 min for standard T2w, and 2:10 min for the proposed sampling scheme.
The regularization parameters $$$\alpha_1$$$ and $$$\alpha_0=2*\alpha_1$$$ and an optimized sampling scheme were selected by repeating the reconstruction of a single slice using 30 different regularization values and 10 different patterns (Fig. 2), respectively. Two radiologists scored (on a scale of 1 (bad) to 5 (excellent)) these images and we chose the sampling pattern by consensus. Coil sensitivity maps were estimated using ESPIRiT [1].
Reconstructed images were quantitatively evaluated with respect to fully sampled data using RMSE (root mean squared error), HFEN (high frequency error norm), SSIM (structure similarity index).
RESULTS
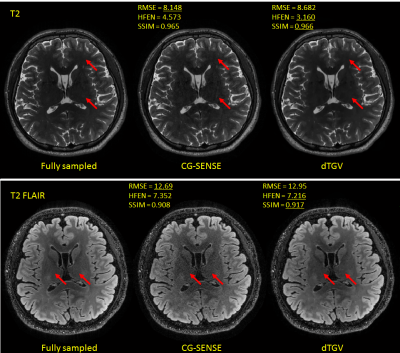
Fig. 3 shows T2w and T2 FLAIR reconstructions using Eq. 2 based on retrospectively undersampled data. For comparison, fully sampled image as well as a conventional conjugate gradient SENSE reconstruction of the undersampled data is shown. Compared to the SENSE reconstruction, dTGV appears less noisy, suppresses the undersampling artifacts visible in the SENSE reconstruction (arrows in Fig. 3) and show comparable quality with the standard acquisition/reconstruction.DISCUSSION
Although visual quality of reconstructed images by dTGV is comparable to those of the fully sampled acquisition, quantitative measures vary to a large extend from subject to subject and reconstruction to reconstruction. Further work is needed to make the proposed dTGV robust to interscan motion by spatial registration of the fully sampled central k-space data.Acknowledgements
No acknowledgement found.References
[1] Uecker et al. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. MRM 2014.
[2] Bredies, Kunisch, and Pock. Total Generalized Variation. SIIMS 2010.
Figures