1761

Analysis of the target gradient method for asymmetric gradient coils
Ashwini Kumnoor1,2, Sebastian Littin2, Feng Jia2, Sairam Geethanath1,3, and Maxim Zaitsev2

1Medical Imaging Research Center, Dayananda Sagar Institution, Bangalore, India, 2Dept.of Radiology,Medical Physics, University of Freiburg, Medical Center, Freiburg, Germany, 3Dept.of Radiology, Columbia University Medical Center, NewYork, NY, United States

Synopsis

Gradient coils are traditionally designed using variations of the target field method. For asymmetric coils it may however be advantages to allow for a flexible field offset and specify the field gradient as a target instead. In this work we evaluate the performance of the target gradient method for generating head gradient inserts with a window in a lower face region.

Introduction

Gradient coil design is traditionally accomplished using a variety of current target field methods (TFM) [1,2], whereby the z-component of the desired encoding field Bz within a target region of interest is specified and a current density on the coil’s current carrying surface is sought using an optimization method of choice. Typically the current carrying surface is represented by a cylinder centered about a spherical or elliptical target region. The current density is typically represented by a stream function, which can easily be converted to a winding pattern by plotting its level lines. A variation of the target field method may easily be derived, which specifies the components of the gradient of Bz in the target region instead of the Bz itself. This has an advantage of a more direct control of the local deviations of the gradient strength, which is of a great relevance for imaging applications. A further advantage of the gradient-based method that it is capable of choosing an optimal center field offset for coils with a non-symmetric or irregular current carrying surfaces. In this study, we evaluate the performance of the target gradient method (TGM) and compare it to TFM on an example of an unshielded head gradient insert with a window in the face region.

Methods

In this study, we have chosen to employ a thin wire approximation [3] as a fast and flexible gradient prototyping method. A cylindrical support surface of a diameter of 38 cm and length of 90 cm was segmented in 32 circumferential and 33 longitudinal cells. Each cell was characterized by a current density flowing in a circumferential direction. A modification of the original method has been derived, which directly calculates the gradients of the current elements instead of their Bz. All coil designs allowed for a gradient strength deviation of 7% within a spherical target volume with a diameter of 10 cm. As a reference, a design was generated with the target volume centered within the coil. All other designs considered a target volume shifted in z-direction towards the patient end of the coil with a distance of 16 cm between the edge of the coil and the center of the target region. Four head gradient configurations were simulated: without a window, with a small window of 16 cm and 30°, medium window of 8 cm and 60° and a large window of 16 cm and 60°. For all configurations and all three gradient directions maximum current and dissipated power were calculated and scaled to the reference symmetric gradient coil. For all coils generated with TGM and TFM design was performed with the field deviation specification from the TGM design.

Results and Discussion

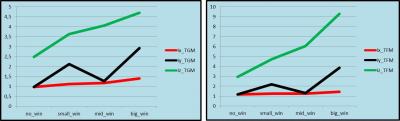
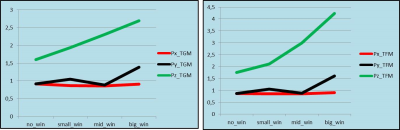
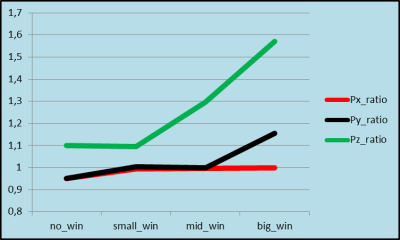
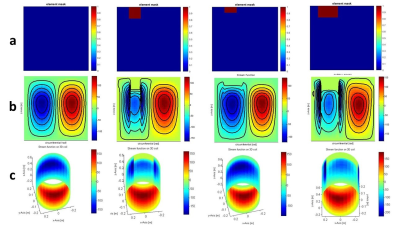
Figure 1 shows the peak current in the coil designs generated by both TGM and TFM, normalized to the symmetric TGM design. As seen, the proximity of the center of the target volume to the coil end readily presents a problem for Gz for a design without a window resulting in a 2.5 and 3 fold increase for the TGM and TFM designs, respectively. Both Gy and Gz are affected by the window, whereas window width presents a larger challenge for Gz, and window height for Gy, respectively, whereas TGM shows a consistently better performance. Figure 2 presents similar data for the power dissipated by the coil and is characterized by similar trends. Figure 3 displays the ratio between the power dissipated by TFM to that of TGM designs. As seen, TGM shows a consistently good performance and appears to be particularly advantageous for Gz. Figure 4 shows examples of different window size along with its stream functions.

In this study, we did not consider force- and torque-balance explicitly, which may be an issue for non-symmetric coils, but it is expected that upon introduction of these constraints TGM will preserve its advantages. Further research is needed to verify the performance of TGM for shielded gradient designs.


Conclusions


Target gradient method is advantageous for a design of gradient coils with a non-symmetric or irregular support for their ability to introduce a global field offset and thereby reduce maximum current and dissipated power.

Acknowledgements

This work was supported, in part, by the ISMRM Research Exchange Program.

References

[1] Lemdiasov RA, Ludwig R. A stream function method for gradient coil design. Concepts Magn. Reson. Part B: Magn. Reson. Eng. 2005 26B:67-80.

[2] Poole M, Bowtell R. Novel gradient coils designed using a boundary element Method. Concepts Magn. Reson. Part B: Magn. Reson. Eng. 2007 31B:162-75.

[3] Littin S, Gallichan D, Welz AM, Jia F, Dewdney A, Weber H, Schultz G, Hennig J, Zaitsev M. Monoplanar gradient system for imaging with nonlinear gradients. MAGMA. 2015 28:447-57.


Figures

Figure 1: Maximum absolute current in the coil designs generated by both TGM (left) and TFM (right) methods, normalized to the symmetric TGM design.

Figure 2: Power dissipated in the coil designs generated by both TGM (left) and TFM (right) methods, normalized to the symmetric TGM design.

Figure 3: Ratio of the power dissipated in the coil designs generated by TFM to that of the TGM design.

Figure 4: Examples of different window sizes shown along with its stream function. (a).Element mask (b).Stream function.(c).Stream function displayed on a 3D coil.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
1761