1757
Design of breast gradient coil with the control of field nonlinearity1Dept. of Radiology, Medical Physics, Medical Center University of Freiburg, Faculty of Medicine, University of Freiburg, Freiburg, Germany, 2Institute of Radiology, University Hospital Erlangen, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 3Medical Physics in Radiology, German Cancer Research Center, Heidelberg, Germany
Synopsis
High performance gradient coils are required to assess the tissue microstructure in human breast in vivo with diffusion-weighted imaging. A deisgn methodology of nonlinear breast gradient coil is proposed to increase resultant gradient strength with the control of field nonlinearity. The method is tested by designing a unilateral breast gradient coil for diffusion weighting. The results are analysis to reveal new insights of coil designs.
Introduction
In order to gain information about the tissue microstructure in human in vivo with diffusion-weighted imaging (DWI), high performance gradient coils would be required. Currently, a local breast gradient coil1 with the gradient strength of 300 mT/m was constructed with a potential application in DWI. This gradient coil was designed to generate a linear encoding field. Recently, a nonlinear gradient coil design methodology2,3 has been proposed to maximize the gradient strength when a target field is unknown, which has been successfully used to design coil elements for localized high resolution imaging applications such as PatLoc4. Up to now, the exact relationship between resultant gradient strengths for the linear and non-linear coil design remains unclear. In this work, an optimization problem is formulated to explore this relationship. One parameter is proposed to assess the performance of different coil designs. The proposed optimization problem and the performance measure are tested by attempting to design a unilateral single-channel breast gradient coil for diffusion weighting. The results of the breast gradient coil design are analyzed to reveal new insights into coil designs.Methods
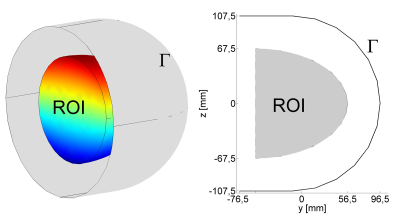
The following design requirements of the gradient coil were considered: firstly, the coil has to generate an encoding field with strong gradients at every test point within a region of interest (ROI). Secondly, the coil inductance should be considered during the coil design in order to reduce switching rates. Thirdly, some engineering constraints, such as wire track width, have to be considered for the practical fabrication of the coil. Finally, non-linearity of resultant field needs to be controlled.
Based on the requirements above, an optimization problem is proposed as follows:
$$\min_{\psi}\mbox{ } F, \mbox{ }F:=-\sum_{\vec{x}_i\in{\text{ROI}}}\left|\nabla B_z(\psi,\vec{x}_i)\right|+\alpha_J \lVert\vec{J}(\vec{x})\rVert_{p}$$
$$\text{subject to}\quad\frac{1}{\mu}\int_{\Gamma^{'}}\int_{\Gamma}\frac{|\vec{J}(\vec{x})\vec{J}(\vec{x}^{'}|}{|\vec{x}-\vec{x}^{'}|}d{\Gamma}d\Gamma^{'}\leq W_{\max}\quad\text{and}\quad|B_z(\vec{x}_i)-B_z^*(\vec{x}_i)|\leq\delta\max|B_z^*(\vec{x})|.$$
Here, $$$\psi$$$ denotes the stream function of the electric current density vector $$$\vec{J}(\vec{x})$$$ where $$$\vec{J}(\vec{x})= \nabla\times(\psi(\vec{x})\vec{n})$$$ on a current-carrying surface $$$\Gamma$$$(Fig. 1) with a normal unit vector $$$\vec{n}$$$. The $$$B_z$$$ is the z-component of the magnetic fields generated by current density $$$\vec{J}$$$ on $$$\Gamma$$$ (Fig. 1) and is calculated using the Biot-Savart law. The $$$B_z^*$$$ is a target magnetic field, which is the linear z-gradient field of 50 mT/m gradient strength in the examples. The points $$$\vec{x}_i=(x_i, y_i, z_i), i=1, …, m$$$, denote the coordinate vectors of $$$m$$$ test points in the ROI, $$$\mu$$$ indicates the vacuum permeability, $$$W_{\max}$$$ denotes a specified maximal magnetic energy of the designed coil which is used to control the coil inductance and δ is a parameter to tune the non-linearity of resultant $$$B_z$$$. The objective function F of the problem (1) consists of two terms. The first one is related to the gradient strength of the encoding fields and the other is applied to control the minimal width of wire tracks of the designed coil by the p-norm (||·||p) method2. One positive constant $$$\alpha_J$$$ is to balance the tradeoff among them.
In order to assess different coil designs, a performance metric is defined as follows:
$$\beta:=\frac{\sum_{\vec{x}_i\in{\text{ROI}}}\lvert\nabla B_z(\psi,\vec{x}_i)\rvert}{m\sqrt{W_{\max}}}$$
Here, the figure of merit β is intended to measure the coil efficiency based on the average of the gradient magnitude of the encoding field over the ROI. From equation of $$$\beta$$$, it is clear that an ideal high-performance coil should have a high $$$\beta$$$. All numerical examples were solved with the function fmincon in MATLAB (The MathWorks. Natick, USA).
Results and Discussion
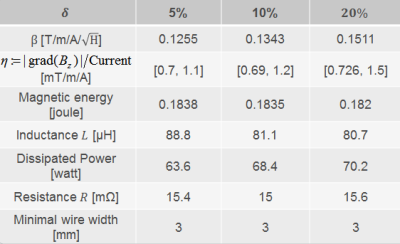
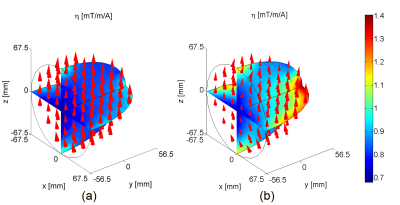
Figure 2 presents the effect of different values of $$$\delta$$$ on the figure of merit, gradient strength per current and other coil properties. As seen, the figure of merit $$$\beta$$$ grows upon the increase of $$$\delta$$$. For example, compared to $$$\delta$$$ = 5%, which is a typical relative error for a linear encoding field, the figure of merit increases by a factor of 1.2 when $$$\delta$$$ = 20%. Considering that the stored magnetic energy of the coils decreases slowly, the large increase of $$$\beta$$$ mainly comes from the variation of gradient strength over the ROI with the increase of $$$\delta$$$. Figure 3 shows the comparison of the gradient strength distributions of the resultant fields between $$$\delta$$$ = 5% and $$$\delta$$$ = 20%. As seen, compared to the case of $$$\delta$$$ = 5%, the gradient strength for $$$\delta$$$ = 20% increases in the most part of the ROI. Especially at the most distant point of the ROI (Fig. 3), the gradient strength for $$$\delta$$$ = 20% increases by a factor of 1.34.Conclusions
The proposed design method is useful to obtain realizable non-linear gradient coils. The proposed performance parameter can be used to quantify resultant gradient strengths for linear and nonlinear gradient coils and assist a decision-maker to determine which a nonlinear coil is suitable for its purpose.Acknowledgements
Financial support by the German Research Foundation (DFG, project number 326944748) is gratefully acknowledged.References
1. van der Velden T, van Houtum Q, Gosselink M, et al., Characterization of a breast gradient insert coil at 7 tesla with field cameras. ISMRM. 2016;p3543.
2. Jia F, Littin S, Layton KJ et al., Design of a shielded coil element of a matrix gradient coil. J Magn Reson. 2017;281:217-228.
3. Littin S, Jia F, Layton KJ et al.,Development and implementation of an 84-channel matrix gradient coil. Magn Reson Med. 2017;doi: 10.1002/mrm.26700.
4. Hennig J, Welz AM, Schultz G, et al., Parallel imaging in non-bijective, curvilinear magnetic field gradients: a concept study. MAGMA. 2008; 21: 5–14.
Figures