Introduction

For decades, fractal geometries have been successfully employed and exploited in the design of antennas for telecommunication systems¹ but to our knowledge this approach has rarely been employed in the design of novel radiofrequency (RF) coils for magnetic resonance imaging (MRI). This is important because engineering and physics research continues to generate new ways to measure biomarkers of lung physiology using hyperpolarized ¹²⁹Xe MRI. However, pulmonary applications of ¹²⁹Xe MRI is exquisitely sensitive to RF coil field (B1⁺) inhomogeneities that often result in signal intensity artifacts which mask the novel information inherent to these unique images². Until now, however, no engineering approaches have been designed or implemented to prospectively correct B1⁺ inhomogeneities. Our objective was to explore fractal geometry in the design of RF coils to minimize B1⁺ inhomogeneities with direct application in hyperpolarized ¹²⁹Xe MRI.

Methods

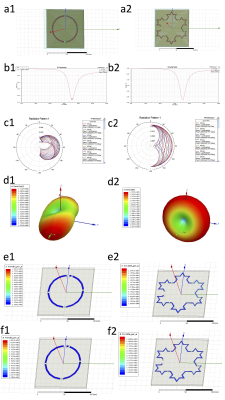
A Koch fractal-shaped micro-strip was selected as it closely resembles a simple circular surface coil. Fig1.a1, a2 shows the circular and fractal design respectively. Both copper micro-strip coils were mounted on a 5mm thick substrate RO4305 with a 20mm thick air radiation box on top. Both coils were tuned to 35.3MHz (¹²⁹Xe frequency at 3T) with 50Ω match, as seen in Fig1.b1, b2. All simulations were performed in HFSS³, which is a well-known finite element solver for electromagnetic structures.

Results and Discussion

The energy radiated by the circular and fractal coils is represented by the radiation pattern on Fig1.c1, c2 in polar coordinates. A radiation pattern defines the variation of the power radiated by an antenna as a function of direction away from the antenna. This power variation as a function of the arrival angle is observed in the antenna's far field on Fig1. d1, d2. Here, it can be observed that the fractal-patterned coil shows a more homogeneous radiation pattern than the circular coil. The electric (e1, e2) and magnetic (f1, f2) field distributions at the surface of the micro-strip conductor for both resonators are shown in Fig.1. It can be seen that the fractal-patterned coil shows relatively higher H field compared to the circular coil. Quantitative measurements of both fields are also presented in Table1. The maximum E field in the surface of the fractal-patterned micro-strip coil is reduced 68% compared to the E field in the circular coil while the mean H field at the surface of the fractal-patterned micro-strip coil is 30% higher and more evenly distributed than the H field from the circular coil. Table1 shows the maximum and mean magnetic field calculated in the air volume adjacent to the coil. In the air volume, the fractal-patterned coil shows relatively higher H compared to the circular coil.

Conclusions

Fractal-patterned MRI coils could offer some improvement in signal penetration and magnetic field homogeneity, while concurrently reducing the electric field. However, further studies including additional patterns and iterations are necessary to determine the optimal geometry design.

Acknowledgements

No acknowledgement found.