1681
On the estimation of the apparent bundle-wise diffusivity profiles for axon damage detection1Computer Science, Centro de Investigacion en Matematicas, Guanajuato, Mexico, 2Institute of Neurobiology, Universidad Nacional Autonoma de Mexico, Queretaro, Mexico
Synopsis
To estimate the physical features of intra-voxel axon bundles in the detection of axon damage it is important to compute bundle-wise apparent diffusivities. There is a first family of methods that factors-out the effects of the orientation-dispersion under a convolution model (e.g. Spherical Mean), and a second family that associates the diffusivity properties with specific orientations (e.g. Gaussian-Mixture-Models). Here we demonstrate that only the second family provides bundle-wise apparent diffusivities, and thus it provides the useful information for clinical applications. This is demonstrated on a broad synthetic validation as well as on ad-hoc rat ex-vivo phantom with a damaged bundle.
Introduction and Purpose
DW-MRI allows studying the white matter (WM) architecture1,8. In voxels containing multiple fibers it is important to estimate their individual diffusion properties in order to identify intra-voxel damaged bundles.2,3 There are two recently proposed methods aimed to estimate the intravoxel Gaussian diffusivity profiles parameterized as the axial ($$$\lambda_{\|}$$$) and radial ($$$\lambda_{\bot}$$$) diffusivities: 1) the Spherical Mean Technique (SMT)4, which utilizes averages of the measurements per $$$b$$$-value to factor out the effects of the orientation dispersion and 2) the Multi-Resolution Discrete-Search method (MRDS)5, which estimates orientations, volume fractions and per-bundle diffusivity profiles. SMT takes into account the orientation dispersion of the fibers, but it does not provide bundle-wise diffusivities, MRDS provides bundle-wise diffusivities, but does not explicitly account for orientation-dispersion. In this work, the capability of bundle-wise damage detection of these two state-of-the-art methods was extensively evaluated on synthetic data and on ad-hoc rat ex-vivo phantom3, where healthy and damaged axon bundles co-exist within the voxels.Methods
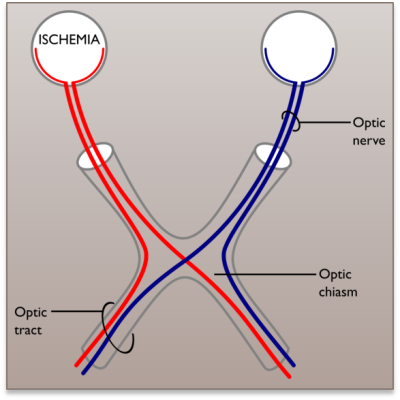
We used the SMT code provided by the authors (https://github.com/ekaden/smt). Two cases were tested on synthetic data with and without dispersion: 1) the intra-voxel-bundles have the same diffusion profile (to simulate normal tissue) and 2) the intra-voxel-bundles have different diffusion properties (simulating one normal and one damaged fiber bundles). The signals without dispersion were simulated using the Gaussian-Mixture-Model (GMM)6; for the data with dispersion, the signal from each tensor (response function) was convolved with a Watson distribution before being added in the GMM. For the dispersed signals, the apparent diffusivities ($$$\lambda^{APP}$$$) were computed by fitting a diffusion tensor to the dispersed/convolved signals associated with a single bundle. For the signals without dispersion $$$\lambda^{APP}=\lambda^{GT}$$$, where $$$\lambda^{GT}$$$ denote the diffusivity profile of the response function. For the Experiment 1, the data were simulated for several intra-voxel configurations with $$$N$$$ bundles $$$N=1,2,3$$$: crossing angles ($$$N=2;40-90^{\circ}$$$, $$$N=3:60-90^{\circ}$$$) and different volume fractions per bundles. $$$\lambda^{APP}_{\|}$$$ and $$$FA^{APP}$$$ were in the ranges of interes $$$[0.0005-0.0019]$$$mm^2/s and $$$[0.70-0.90]$$$, respectively. For Experiment 2, two-fiber signals with crossing angles in the range $$$60-90^{\circ}$$$ were simulated in a way that one fiber bundle had normal diffusivity properties ($$$\lambda_{\|}^{APP}=0.0017$$$ and $$$FA^{APP}=0.799$$$), and the other was computed for several degrees of damage ($$$\lambda_{\|}^{APP}$$$ and $$$FA^{APP}$$$ in the ranges $$$[0.0011-0.0017]mm^2/s$$$ and $$$[0.5,0.799]$$$, respectively). For the signals without dispersion, the tissue damage was simulated by changing the apparent GMM eigenvalues and for the dispersed signals the response functions were fixed and the dispersion was increased. For all the synthetic experiments, 50 DW signals with b-value=1000 $$$s/mm^{2}$$$, 50 with b-value=3000 $$$s/mm^{2}$$$, and 10 $$$S_{0}$$$ with SNR=20,30 were used. The ex-vivo data3 contain15 rat brains, retinal ischemia was induced in one optic nerve for 11 rats allowing the study of the per-bundle-diffusion-properties in the optic chiasm where the optic nerves cross, see Figure 4; the other 4 healthy rats are used as control group. The ex-vivo acquisition protocol contains 80 DW signals with b-value=2000 $$$s/mm^{2}$$$, 80 with b-value=2500 $$$s/mm^{2}$$$, and 20 $$$S_{0}$$$ signals.Results
The results for the synthetic Experiments 1 and 2 are shown in Figures 1 and 2, respectively. Figure 1 shows that even with dispersion MRDS is stable, while SMT shows larger errors even for the cases without dispersion. Figure 2 shows MRDS correctly estimates the different diffusion properties for both cases, with and without dispersion, SMT was not able to differentiate them and showed larger error w.r.t. the bundle's apparent diffusivities. Figure 3 shows the results for the ex-vivo data, for MRDS the estimated diffusivities are plotted for both optic-nerves and both optic-chiasm-bundles, the results show that the parameters estimated by MRDS allow to differentiate between the normal and damaged bundles for the ischemic rats, while in the control rats there were not significant changes between the diffusivities of the fiber bundles. For SMT, the diffusivities were plotted for both optic-nerves and the optic-chiasm, the results show that SMT tends to estimate sticks ($$$\lambda_{\bot}^{APP}≈0$$$) and does not allow for the identification of the normal and damaged bundles, the limitation above can be appreciated in the FA maps of both methods on Figure 5.
Conclusions
Our experiments indicate that the local microstructure diffusivity profiles computed by SMT are not suitable to detect axon-bundle damages at heterogeneous voxels, i.e., the bundle-wise apparent diffusivity profiles that may be computed using Gaussian-Mixture-Modeling. As demonstrated by the ex-vivo experiments the SMT diffusivity profiles (nearly sticks) do not contain information about the microstructure differences per bundle, where such information is vital for clinical applications because SMT cannot associate diffusivity profiles to bundles (compartments7). On the other hand, this association, which permits the differentiation of healthy and damaged bundles, may be successfully performed by the MRDS technique.
Acknowledgements
LC was partially funded by PAPIIT/DGAPA (IG200117). ARM and JLM were partially supported by SNI-CONACYT, Mexico, (Grants 169338 and 6243). GRV and RCL were supported by scholarships from CONACYT, Mexico. C-LR, R-MA, MJL, LC, R-VG and N-IR were supported by the Laboratorio Nacional INB-UNAM-CIMAT project from CONACyT.
References
1. Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys. J. 1994;66(1):259–67.
2. Alexander D.C. Multiple-fiber reconstruction algorithms for diffusion MRI. Ann NY Acad Sci., 2005, 1064(1),113-33.
3. Concha L., Larriva-Sahd J., et al. Diffusion MRI of axonal degeneration in areas of fiber crossing: Histological correspondence. ISMRM 2017 Hawaii, USA, #3814.
4. Kaden E., Kruggel F., et al. Quantitative mapping of the per‐axon diffusion coefficients in brain white matter. Magn Reson Med. 2016, 75(4): 1752-1763.
5. Coronado-Leija R., Ramirez-Manzanares A. et al. Estimation of individual axon bundle properties by a Multi-Resolution Discrete-Search method. Medical Image Analysis . 2017, 42(1), 26-43.
6. Tuch D.S., Reese T.G. High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magnetic resonance in medicine, 2001, 48(4), 577-582.
7. Panagiotaki E., Schneider T., et al. Compartment models of the diffusion MR signal in brain white matter: A taxonomy and comparison. NeuroImage. 2012; 59(3): 224-2254.
8. Zhang H., Schneider T., et al. NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage. 2012; 61(4): 1000-1016.
Figures
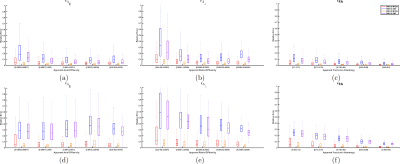
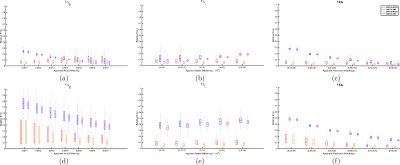
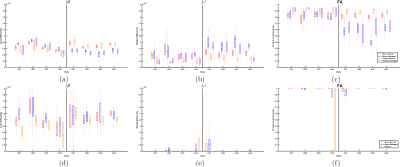
Figure 2. Relative errors of the diffusivities obtained by MRDS and SMT for Experiment 2 (two fiber bundles, one normal and the other damaged). (a)-(c) Results for data without dispertion and different diffusivities per bundle, MRDS was able to estimate the apparent diffusivities with smaller errors than SMT, the quality decreases as the differences between bundles increases. (d)-(f) Results for data with same diffusivities and different dispersions per bundle, although its results were degraded because of the dispersion, MRDS was able to estimate correctly the bundle-wise apparent diffusivities, while SMT reported the same diffusivities in all cases without detecting the damage.