1679
Measuring water exchange using cumulant expansions1Harvard Medical School, Boston, MA, United States, 2Brigham and Women's Hospital, Boston, MA, United States, 3Lund University, Lund, Sweden
Synopsis
Diffusion MRI (dMRI) can provide important information about water exchange between different tissue compartments. In this abstract, we introduce a generalized model to measure the exchange rate using arbitrary gradient sequences. We present a unified theory that incorporates water diffusion and exchange as a stochastic diffusion-exchange process. Our work for the first time allows to compare different diffusion sequences and allows to determine the optimal experimental configurations to measure the exchange rate. In the most common situation with single- or double-diffusion encoding (SDE, DDE) sequences, our theory shows that DDE is more sensitive to water exchange at short time scale. We validate our theory using Monte-Carlo simulations.
Introduction
The standard approach for measuring water exchange is the Kärger model1 which uses a single diffusion encoding (SDE) sequence. Recent experiments suggested the potential benefit of using a DDE sequence with the so-called filter exchange imaging (FEXI) method2. Both these measurement techniques are sequence dependent and the field lacks a general biophysical model that is independent of the measurement technique. To overcome this limitation, we propose a general cumulant expansion of dMRI signals for any type of gradient sequences. In the special case of SDE and DDE, the proposed solution provides new insights about the difference between dMRI signals from the two sequences at different time scales.
Theory
Diffusion-and-exchange process: We consider a stochastic differential equation that models the microscopic-scale motions of water molecules described by
$$d x(t)=\sigma(x(t))dw(t)$$
where $$$x(t)$$$ denotes the position of a water molecule, $$$w(t)$$$ denotes the standard Wiener process and $$$\sigma(x(t))$$$ characterizes the underlying diffusivity of tissue components with $$$\sigma(x(t))=2D_1, 2D_2$$$ when $$$x(t)$$$ belongs to the two tissue components, respectively. Moreover, the molecules exchang between the two components with their probability distribution evolving according to
$$\frac{d}{dt}p(t)=Kp(t)$$
with $$$K=[-k_{12}, k_{21}; k_{12}, -k_{21}]$$$. To simplify the analysis, we consider the situation with isotopic diffusivity and with only two tissue components, though the theory can be extended to more general situations. We note that the assumption of static diffusivity is well-founded as the diffusion coefficient changes with time only at short time-scales and converges to the ``bulk" diffusion coefficient $$$D_\infty$$$ at long time scales3. The proposed microscopic stochastic model of diffusion-and-exchange processes not only explains the evolution of the ensemble average propagator provided by the Kärger model for narrow-pulsed SDE sequences, but also provides a solution for computing dMRI signals for any type of sequences.
On the cumulant expansion: Let $$$\phi(T)=\int_0^T g(t)x(t)dt$$$ denote the phase change of a diffusing spin under a gradient sequence $$$g(t)$$$ with $$$t\in[0, T]$$$. Since the proposed SDE model provides the probability distribution of the entire trajectory $$$x(t)$$$, all the statistical moments of $$$\phi(T)$$$ can be theoretically computed. Specifically, we show that the cumulant expansion for the dMRI signals is given by
$$\ln S(b)\approx -\bar D b+\tfrac12 Var(D) h(\cdot) b^2,$$
where $$$\bar D$$$ and $$$Var(D)$$$ denote the mean and variance of the diffusivities, respectively, and $$$h(\cdot)$$$ quantifies the sensitivity of the pulse sequence to water exchange which is defined as
$$h(\cdot):=2\int_0^Te^{-kt} q_4(t)dt,$$
with $$$q_4(t):=\frac{1}{b^2}\int_0^T q^2(s) q^2(s+t)ds$$$ with $$$q(t)=\int_0^t g(s)ds$$$, and $$$k=k_{12}+k_{21}$$$. Moreover, for $$$kT\ll 1$$$, it can be further simplify that $$$h(\cdot)\approx 1- kT_{ex}$$$ with $$$T_{ex}=2\int_0^T t q_4(t)dt$$$.
For SDE sequences, we have
$$T_{ex, {\rm SDE}}=\tfrac13 f(\delta,\Delta),$$
with $$f(\delta,\Delta)=(\Delta-\tfrac13 \delta)^{-2}(\Delta^3-\Delta^2\delta+\tfrac23 \delta^2 \Delta-\tfrac{4}{21}\delta^3)\approx (\Delta-\tfrac13\delta).$$
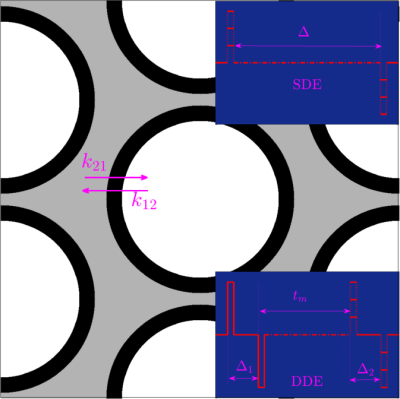
For the FEXI-type DDE sequence shown in Fig. 1 with $$$\Delta_1=\Delta_2$$$, the corresponding $$$T_{ex}$$$ is given by
$$T_{ex,{\rm DDE}}=\tfrac{b_1^2+b_2^2}{b^2}f(\delta,\Delta)+\tfrac{2b_1b_2}{b^2}(\Delta_1+t_m)\approx \tfrac{b_1^2+b_2^2+6b_1b_2}{3b^2} \Delta_1+\tfrac{2b_1b_2}{b^2}t_m-\tfrac{b_1^2+b_2^2}{9b^2}\delta.$$
Comparing SDE and DDE signals: We used the above cumulant expansions to analyze the sensitivity of SDE and DDE signals to water exchange. To this end, we constrain the diffusion time to $$$T\in[T_{\rm min}, T_{\rm max}]$$$ and the maximum b-value to $$$b_{\rm max}$$$. Then, we compare the maximal signal differences $$$e_{\rm SDE}=\ln S(b_{\rm max},T_{\rm min})-\ln S(b_{\rm max},T_{\rm max})$$$ for the two types of sequences. For simplicity, we consider the situation with narrow-pulses.
At long-time scale, i.e. $$$kT_{\rm max}\gg 1$$$, we obtain
$$ e_{\rm SDE}\approx \tfrac12 Var(D)(1-\tfrac13kT_{\rm min}) b_{\rm max}^2,$$
$$ e_{\rm DDE}\approx \tfrac14 Var(D)(1-\tfrac13kT_{\rm min}) b_{\rm max}^2.$$
On the other hand, if $$$kT_{\rm max}\ll 1$$$, the signal differences are given by
$$ e_{\rm SDE}\approx \tfrac16 Var(D) k(T_{\rm max}-T_{\rm min})b_{\rm max}^2,$$
$$ e_{\rm DDE}\approx \tfrac14 Var(D) k(T_{\rm max}-T_{\rm min})b_{\rm max}^2,$$
respectively. Moreover, the optimal $$$e_{\rm DDE}$$$ is obtained when $$$\Delta_1=\tfrac12T_{\rm min}$$$ and $$$b_1=\tfrac12 b_{\rm max}$$$.
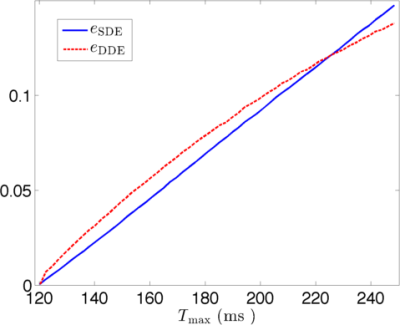
Thus, $$$e_{\rm SDE}< e_{\rm DDE}$$$ at short-time scale and $$$e_{\rm SDE}> e_{\rm DDE}$$$ at long-time scale.
Experiment
The proposed theoretical results were validated using Monte-Carlo simulations based on a synthetic structure, as shown in Fig. 1, using the approach described in4. The intra-to-extra and extra-to-intra exchange rates are given by $$$k_{12}=0.0032 {\rm ms}^{-1}$$$, and $$$ k_{21}=0.0072 {\rm ms}^{-1} $$$, respectively. The simulated diffusivity was equal to $$$3 {\rm \mu m^2/ms}$$$. Based on the simulated trajectories, we computed the dMRI signals with $$$T_{\rm max}\in[120, 240] {\rm ms}$$$ and $$$b_{\rm max}=20 {\rm ms/\mu m^2}$$$.Results
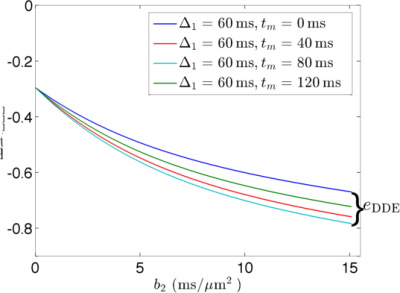
Fig. 2 and Fig. 3 show the simulated dMRI signals for narrow-pulse SDE and DDE sequences, respectively, with different diffusion times. Fig. 4 compares $$$e_{\rm SDE}$$$ with $$$e_{\rm DDE}$$$ for different $$$T_{\rm max}$$$. As expected, dMRI signals from DDE sequences are more sensitive to exchange at a relatively short-time scale but SDE sequence can provide larger contrast at long-time scales.Acknowledgements
Work in this abstract was supported in part by NIH grants under R01MH097979 (PI: Rathi), R01MH111917 (PI:Rathi), R01MH074794(PI:Westin).
References
[1]. J. Kärger, NMR self-diffusion studies in heterogeneous systems, Adv Col- loid Interface Sci 23 (1985) 129–148.
[2]. S. Lasič, M. Nilsson, J. Lät, F. Ståhlberg, D. Topgaard, Apparent exchange rate mapping with diffusion MRI, Magn. Reson. Med. 66 (2) (2011) 356– 365.
[3]. L. Ning, K. Setsompop, C.-F. Westin, Y. Rathi, New insights about time- varying diffusivity and its estimation from diffusion MRI, Magn. Reson. Med. 78(2) (2007) 763-774.
[4]. M. Nilsson, E. Alerstam, R. Wirestam, F. Støahlberg, S. Brockstedt, J. Lätt, Evaluating the accuracy and precision of a two-compartment Käger model using Monte Carlo simulations, J. Magn. Reson. 206 (1) (2010) 59–67.
Figures