Synopsis

Recent studies showed that PCA denoising algorithms using random matrix theory provide an optimal compromise between noise suppression and loss of anatomical information for standard diffusion measures and tractography approaches. In this study, we show that this algorithm seems also to optimally preserve the non-Gaussian diffusion properties. Several factors that influence the performance of the PCA denoising algorithm are also assessed, such as the spatial heterogeneity of diffusion parameters across neighbour voxels and different scanning protocols. Moreover, the compatibility of PCA denoising with Gibbs artefact suppression and noise bias correction is evaluated.

Introduction

Theory

Assuming that $$$X$$$ is a $$$M×N$$$ matrix containing the $$$N$$$ diffusion-weighted measures for $$$M$$$ neighbour voxels, the local PCA can be performed from the eigen-decomposition of the covariance matrix $$$C$$$:

$$C=\frac{1}{M}X^TX=\frac{1}{M}U\Lambda U$$ (1)

where $$$U$$$ is the matrix containing the eigenvectors of $$$C$$$ and $$$\Lambda$$$ is a diagonal matrix containing its eigenvalues $$$\lambda$$$. The eigenvalues corresponding to the noise components can be identified by finding the number of low-intensity eigenvalues that best fit the Marčenko-Pastur distribution¹:

$$P(\lambda)=\frac{\sqrt{(\lambda_+-\lambda)(\lambda-\lambda_-)}}{2\pi \gamma\lambda\sigma^2}$$ (2)where $$$\sigma$$$ is the raw data noise standard deviation, $$$\gamma=\frac{N}{M}$$$ and $$$\lambda_\pm=\sigma^2(1\pm\gamma^{1/2})^2$$$. The denoised version of $$$X$$$ can then be computed as:

$$X_D=XU_pU_p^T $$ (3)

where $$$U_p$$$ is a matrix containing only the signal component eigenvectors.

Methods

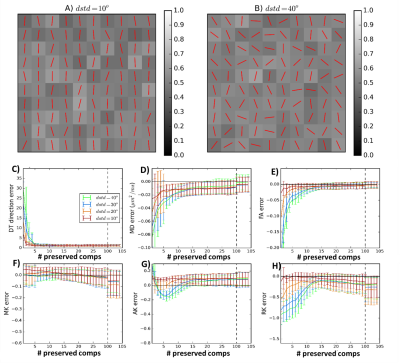
In-silico: PCA denoising is first evaluated in synthetic phantoms so that factors that may impact the algorithm performance (i.e. different diffusion acquisition protocols and different levels of diffusion heterogeneity between neighbour voxels) are assessed in a controlled fashion (Fig.1A-B). Phantoms are used to perform three experiments:

1.Finding the optimal number of preserved components: Phantoms corrupted by Rician noise (nominal SNR=20) are first decomposed into principal components (Eq.1). Then, different phantom versions are reconstructed for different numbers of components (Eq.3). The optimal number of preserved components is associated with the phantom version that presents the lowest errors in diffusion measurements. Non-gaussian diffusion is quantified using three diffusion kurtosis imaging (DKI) measures: mean kurtosis (MK), axial kurtosis (AK), and radial kurtosis (RK)².

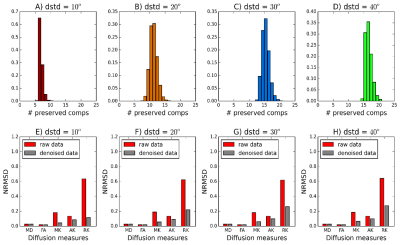
2.Evaluating the number of signal components preserved by PCA denoising: The PCA algorithm is then applied to the noise-corrupted phantoms. The random matrix classifier has optional performance if the number of signal components detected matches the number of preserved components determined in experiment 1.

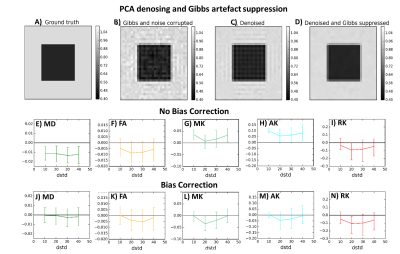
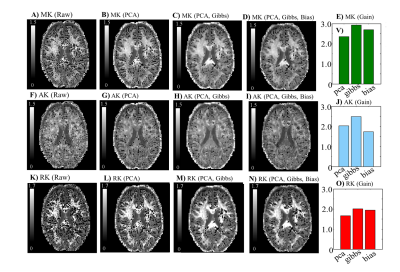
3.Evaluating the compatibility with other pre-processing techniques: denoising does not remove Rician signal bias nor MRI artefacts. Therefore, the performance of the Rician bias inversion technique³ is evaluated in denoised phantoms. Moreover, the combination of PCA denoising and a sub-voxel shift unringing algorithm is tested in phantoms corrupted by Gibbs artefacts⁴ (Fig.3A-C).

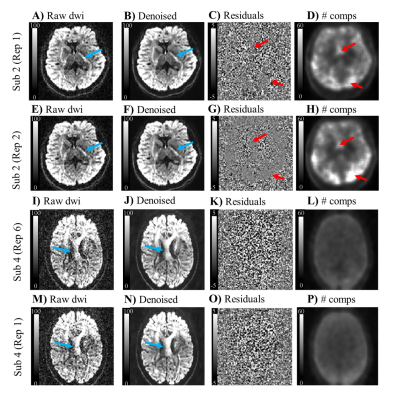
In-vivo: Dataset of two human brains were acquired on a 3T Siemens Prisma scanner using a twice-refocus spin-echo sequence. The two datasets were acquired based on different diffusion parameters: 1.Long protocol - b-values of 300, 1000, and 2000 s/mm² along 8, 30, and 60 directions respectively and two b-value=0 images; 2.Fast protocol - b-values of 1000 and 2000 s/mm² for 30 directions and two b-value=0 images. To estimate the denoising gain ($$$SNR_{denoised}/SNR_{raw}=\sigma_{raw}/\sigma_{denoised}$$$), protocol 1 and 2 were repeated 4 and 7 times.

Results and Discussion

Simulations:

1) Optimal number of preserved components: The profiles of errors as a function of the number of preserved components seems to be different for each diffusion measure and seems to depend on the level of the neighbour voxel heterogeneity (Fig.1C-H).

2) Number of signal components preserved by PCA denoising: The random matrix theory classifier successfully detects a larger number of signal components for phantoms with higher neighbour voxel heterogeneity (Fig.2A-D). Denoising seems to decrease the errors of DKI's measurements but no denoising benefits were observed for DTI metrics (Fig2.E-H).

3) Compatibility with other pre-processing techniques: The combined use of Denoising and Gibbs unringing seems to successfully suppress noise and Gibbs artefacts (Fig.3.A-D). Noise bias correction seems to decrease the biases of DTI measures. However, this algorithm seems to slightly increase the error variance of DKI measures (Fig3.E-N).

In-vivo: The denoising performance seems to depend on volume misalignment induced by motion, particularly for the data acquired with the long protocol (Fig.4). As predicted by simulations, the combined use of Denoising and Gibbs unringing seem to induce the higher SNR gains for DKI measures (Fig.5).

Conclusion

Acknowledgements

References

1. Veraart J, Novikov DS, Christiaens D, et al. Denoising of diffusion MRI using random matrix theory. Neuroimage 2016:146, 394-406. doi: 0.1016/j.neuroimage.2016.08.016.

2. Tabesh A, Jensen JH, Ardekani BA, Helpern JA. Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magn. Reson. Med. 2011:65(3); 823–836. doi:10.1002/mrm.22655

3. Koay CG, Basser PJ. Analytically exact correction scheme for signal extraction from noisy magnitude MR signals. J Magn Reson 2006:179; 317–322. doi:10.1016/j.jmr.2006.01.016

4. Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magn. Reson. Med. 2016:76(5); 1574–1581doi: 10.1002/mrm.26054