1653

Efficient Reconstruction of Diffusion Kurtosis Imaging Based on a Hierarchical Convolutional Neural Network
Ting Gong1, Hongjian He1, Zhiwei Li2, Zhichao Lin2, Qiqi Tong1, Chen Li1, Yi Sun3, Feng Yu2, and Jianhui Zhong1,4

1Center for Brain Imaging Science and Technology, Key Laboratory for Biomedical Engineering of Ministry of Education, College of Biomedical Engineering and Instrumental Science, Zhejiang University, Hangzhou, China, 2Department of Instrument Science & Technology, Zhejiang University, Hangzhou, China, 3MR Collaboration NE Asia, Siemens Healthcare, Shanghai, China, 4Department of Imaging Sciences, University of Rochester, Rochester, NY, United States

Synopsis

Diffusion kurtosis imaging (DKI) captures more complex microstructural properties than the widely used diffusion tensor imaging (DTI) but requires a longer acquisition time. To accelerate its acquisition, and thus facilitate its practical clinical use, a hierarchical convolution neural network (H_CNN) reconstruction method was proposed. The results showed that the H_CNN method provides efficient reconstruction of all eight DTI and DKI measures using as few as nine DWIs, with improved robustness against noise and the retention of fine structures, compared to artificial neural network-based methods. The H_CNN method potentially enables DKI clinical applications with an acquisition time of one minute.

Introduction

Diffusion kurtosis imaging (DKI)-derived measures 1 are indicators of microstructural complexity in many diseases 2. They significantly extend the diffusion tensor imaging-based biomarkers at the cost of extended acquisition and post-processing. An artificial neural network (ANN)-based q-space deep learning (q-DL) method that allows a direct estimation of the diffusion measures from efficiently reduced diffusion-weighted images (DWIs) 3 has been proposed. We hypothesized that consideration of the spatial correlation among voxels and a customized network structure could further improve the deep learning-based reconstruction of DKI.

Method

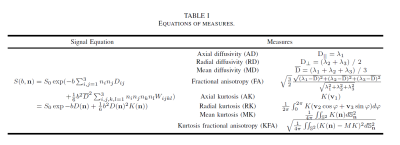
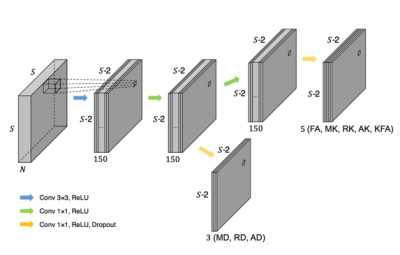
In the DKI model, the signal equation and eight important measures are defined in Table 1. To exploit the commonalities among the measures and improve the generalizability 4, all eight measures were output together in a single network. Since adjacent voxels typically share a similar micro-tissue structure, using the intrinsic spatial correlation of neighboring voxels achieves better statistical power. 5 Considering the above discussion, we proposed a CNN-like network with a partially shared hierarchical structure to make use of the correlation of spatial neighborhoods and target measures, which we called a hierarchical convolutional neural network (H_CNN). An overview of the proposed H_CNN is presented in Figure 2.

The ethics committee of the local institute approved this human study. MRI data were collected on a MAGNETOM Prisma 3T MR scanner (Siemens Healthcare, Erlangen, Germany) equipped with a 64-channel head-neck coil. Three healthy subjects were scanned over three repetitions with a simultaneous-multi-slice EPI sequence: TR/TE=5400/71 ms; FOV=220 × 220 mm2; resolution = 1.5 × 1.5 × 1.5 mm3; number of slices = 93; and SMS factor = 3. Diffusion weightings of b = 1000, 2000, and 3000 s/mm2 were applied in 30 directions respectively 6, with six b=0 volumes equally entered, resulting in 96 DWIs. Images of both opposite phase-encoding directions were acquired.

Image preprocessing for motion and distortion correction as well as alignment across the three scans were conducted in FSL (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/). 7, 8 DKI model fitting was performed using a constrained linear least-square method implemented in DKE (http://academicdepartments.musc.edu/cbi/dki/dke.html). 9 The averaged results of three fully sampled model outputs were taken as the ground truth. Two of the subjects’ data were used as the training set, and the third was used as a test set. Keras 10 was used for training and testing with Tensorflow 11 running backend. All the codes were run on a platform with an NVIDIA GTX-1080 graphics card and the CUDA Deep Neural Network library 12 installed.

Results&Discussion

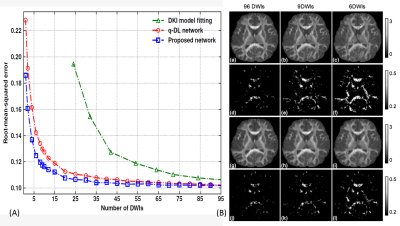
As shown in Figure.3, the H_CNN achieved good estimation performance, even when the number of DWIs decreased to nine. In contrast, the conventional DKI fitting method would be underdetermined with fewer than 24 DWIs. Figure 4 demonstrates the superiority of the H_CNN structure. Both the CNNs and ANNs with more than three hidden layers had higher capacities than the needed capacity of the estimation task, and the CNNs always achieved an approximately 8% improvement on the root-mean-squared error. In addition, the table shows that by separating the scalar measures into two different depths based on complexity, the hierarchical structure achieves a lower root-mean-squared error on all the scalar measures than the CNNs with two or three hidden layers.

As shown in Figure 5, errors of the H_CNN were lower than those of the q-DL, and the gap increased from 0.0003 to 0.04 when the DWIs decreased from 96 to only 1. An overall error of 0.124 with 6 DWIs in the H_CNN is comparable to the error of 12 DWIs in the q-DL network. When the number of DWIs was reduced, the RK difference maps from the q-DL network became much noisier, with smaller values in some white matter skeletons, resulting in a lower contrast to gray matter and loss of some subtle structures. Both the numerical and graphical results showed that the proposed H_CNN outperformed the q-DL network. Although a visually comparable performance could be achieved with only 6 DWIs, a more modest choice of 9 DWIs is recommended to retain some fine structures.

In this study, subsampled DWIs were used as inputs. A subject for future research would be training a network with b-values and directions as auxiliary information that is applicable to various subsampling schemes, thus improving the generalizability.

Conclusion

By introducing the convolution kernels and partially shared structure, we proposed the H_CNN as a more efficient reconstruction method for DKI, with only 9 DWIs required in a one-minute acquisition time. The hierarchical structure can be applied to other complex models with multiple related targets, which may further extend its potential applications.

Acknowledgements

This work was supported by the National Key R&D Program of China (2017YFC0909200), National Natural Science Foundation of China (81401473, 91632109) and the Fundamental Research Funds for the Central Universities (2017QNA5016).

References

1. Jensen J H, Helpern J A, Ramani A, et al. Diffusional kurtosis imaging: The quantification of non‐gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine, 2005, 53(6): 1432-1440.

2. Steven A J, Zhuo J, Melhem E R, et al. Diffusion Kurtosis Imaging: An Emerging Technique for Evaluating the Microstructural Environment of the Brain. American Journal of Roentgenology, 2014, 202(1).

3. Golkov V, Dosovitskiy A, Sperl J I, et al. q-Space Deep Learning: Twelve-Fold Shorter and Model-Free Diffusion MRI Scans. IEEE Transactions on Medical Imaging, 2016, 35(5): 1344-1351.

4. Caruana R. Learning Many Related Tasks at the Same Time with Backpropagation. neural information processing systems, 1995: 657-664.

5. Zhu T, Hu R, Tian W, et al. SPatial REgression Analysis of Diffusion tensor imaging (SPREAD) for longitudinal progression of neurodegenerative disease in individual subjects. Magnetic Resonance Imaging, 2013, 31(10): 1657-1667.

6. Caruyer E, Lenglet C, Sapiro G, et al. Design of multishell sampling schemes with uniform coverage in diffusion MRI. Magnetic Resonance in Medicine, 2013, 69(6): 1534-1540.

7. Andersson J L, Sotiropoulos S N. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage, 2016: 1063-1078.

8. Jenkinson M, Bannister P R, Brady M, et al. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage, 2002, 17(2): 825-841.

9. Tabesh A, Jensen J H, Ardekani B A, et al. Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magnetic Resonance in Medicine, 2011, 65(3): 823-836.

10. Chollet F et al., “Keras,” https://github.com/fchollet/keras, 2015.

11. Abadi M, Barham P, Chen J, et al. TensorFlow: a system for large-scale machine learning. operating systems design and implementation, 2016: 265-283.

12. Chetlur S, Woolley C, Vandermersch P, et al. cuDNN: Efficient Primitives for Deep Learning. arXiv: Neural and Evolutionary Computing, 2014.

Figures

Table 1. DKI signal equation with diffusion strength b along the diffusion direction and eight derived measures. Dij represent elements of the second-order diffusion tensor (DT), and Wijkl represent elements of the fourth-order kurtosis tensor, resulting in 21 unknowns. The eight measures, including diffusivity-related AD, RD, MD, and FA and kurtosis-related AK, RK, MK, and KFA indices, were computed after signal model fitting. λi and vi are the eigenvalues and corresponding eigenvectors of DT, with λ1 being the largest eigenvalue. S2 is the unit sphere. AD, RD, and MD are comparatively simpler than the other measures.

Figure 2. Illustration of the H_CNN structure. S is the size of the image slice and N is the number of subsampled DWIs. The input layer comprises 3 × 3 voxel patches for training and S × S for inference. All the hidden layers were convolutional layers with 150 kernels, followed by rectified linear unit (ReLU) activations. The kernel size is 3 × 3 for the first hidden layer and 1 × 1 for the other hidden layers. MD, RD, and AD are output at the second hidden layer and the other measures are output at a deep layer.

Figure 3. The eight scalar measures estimated by H_CNN and model fitting. From top to bottom: the reference standard as an average of three model fitting results with 96 DWIs (96*3 DWIs), model fitting results with 42 DWIs, model fitting results with 24 DWIs, and estimation results of the H_CNN with nine DWIs. From left to right: MD, RD, AD, FA, MK, RK, AK, and KFA. The model fitting results were easily affected by noise when a reduced number of DWIs was used, particularly for the later five more complex measures.

Figure 4. Demonstration of the H_CNN structure. (A) Overall root-mean-squared errors for the ANNs and CNNs with different depth. Both networks achieved best performance with two or three hidden layers. (B) Root-mean-squared errors of each measure estimated by the CNNs with different depths and the proposed H_CNN. The diffusivity-related measures (AD, MD, and RD) estimated by the CNN with two hidden layers had smaller errors than the CNN with three hidden layers; the other measures (FA, AK, MK, RK, and KFA) showed the opposite results. With a hierarchical structure, all the measures from the H_CNN achieved best performance.

Figure 5. Comparison of the H_CNN and q-DL performance. (A) Root-mean-squared errors over all eight measures of the DKI model fitting, q-DL network, and proposed H_CNN with subsampled DWIs. (B) Maps of radial kurtosis estimated by the q-DL network (a-c) and the proposed H_CNN (g-i) with different numbers of DWIs. Their difference maps to the reference standard are shown in (d-f) and (j-l).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
1653