1648
Error estimation and evaluation of spatial smoothing processing for diffusion kurtosis imaging1Research & Development Group, Hitachi, Ltd., Tokyo, Japan, 2Healthcare Business Unit, Hitachi, Ltd., Tokyo, Japan
Synopsis
DKI often suffers from error estimation such as unphysical negative kurtosis values which result in black voxels on mean kurtosis (MK) map. In this study, causes of the estimation error are investigated by using simulation. In addition, effect of smoothing processing is quantitatively evaluated in terms of reduction in estimation error and image sharpness. Our findings will be useful for clinical diagnosis using DKI.
Purpose
Diffusion kurtosis imaging (DKI) characterizes a degree of non-Gaussian diffusion in order to better understand tissue microstructures.1 DKI has already been successfully used in a wide range of clinical studies.2, 3 However, DKI often suffers from estimation error such as unphysical negative kurtosis values, which result in black voxels on mean kurtosis (MK) map.4 The cause of the error is unknown, and conventionally spatial smoothing is applied in the processing pipeline of DKI to reduce the error. The smoothing blurs MK map and jeopardizes clinical value. In this study, causes of the estimation error are investigated by using simulation. In addition, effect of smoothing processing is quantitatively evaluated in terms of reduction in estimation error and image sharpness.Method
Influence of signal noise and Gibbs ringing artifact on estimated DKI parameters were investigated, respectively. In DKI metric, diffusion signal intensity S(b) is described by the following equation (1).
$$ S(b)=S(0) \exp\left[-bD_{app}+\frac{1}{6}b^{2}D_{app}^2K_{app}\right]\quad\quad\text{(1)}$$
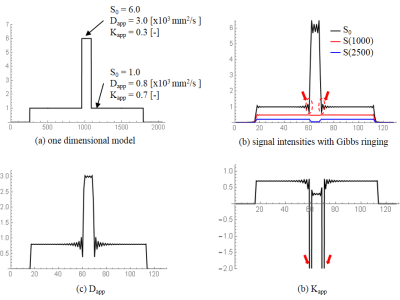
where S(0) is the signal without applying any diffusion gradient, b is the b-value, Dapp is the apparent diffusion coefficient, and Kapp is the apparent kurtosis coefficient. An influence of signal noise was evaluated by using Monte Carlo simulations. The model parameters (S(0), Dapp, and Kapp) were designed to satisfy the following conditions: S(0) = 1.0, signal noise is a normal distribution with zero mean and variance of 0.01, Dapp ≥ 0, Kapp ≥ 0, bmax (= 2500 s/mm2) ≤ 3 / (Dapp Kapp). An influence of Gibbs ringing artifacts was evaluated by following simulation steps. Step 1: A one dimensional model consisted of 2048 points including two objects which have different model parameters respectively was designed. Step 2: three diffusion signal intensities (S(0), S(1000), and S(2500)) of the model were calculated by using equation (1). Step 3: These calculated signal intensities were Fourier-transformed and 128 points were extracted from the center of k-space. Step 4: The extracted data was inverse-Fourier-transformed to obtain signal intensities with Gibbs ringing artifact. Step 5: DKI parameters were estimated by using the signal intensities obtained from Step 4.
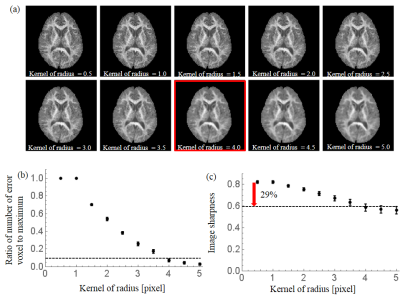
For evaluation of spatial smoothing processing, two-dimensional spin-echo diffusion-weighted (DW) echo planner imaging (EPI) was performed on five healthy volunteers using a 1.5 T MRI system (ECHELON Vega, Hitachi Ltd., Japan). Images of 21 gradient directions and three b-values (0, 1000, and 2500 s/mm2) were obtained. Gaussian filters with different kernel of radius were applied to the obtained images. The error was evaluated by counting voxels with negative kurtosis values. Image sharpness were calculated by using frequency domain method.5
Results
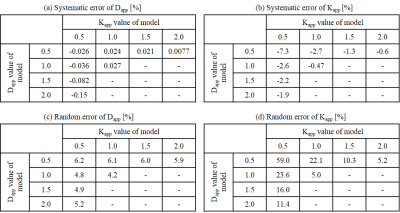
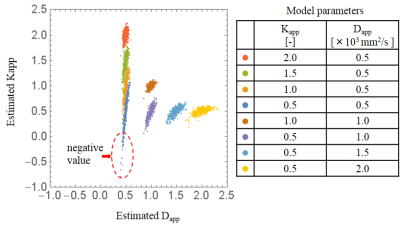
Systematic error and random error of DKI parameters, estimated by Monte Carlo simulations, are shown in Table 1. The systematic error and random error of estimated Kapp are larger than those of estimated Dapp and becomes larger when Dapp and Kapp of the model are smaller. The results shows that estimated Kapp is more affected by signal noise rather than estimated Dapp. The distribution of estimated DKI parameters are shown in Figure 1. The negative kurtosis value occurs when Dapp and Kapp of the model are smaller.
DKI parameters obtained from Gibbs ringing simulation are show in Figure 2. The negative kurtosis value occurs when strong amplification occurs in signal intensity. The large difference in the model parameters, particularly S(0), between neighboring objects tend to cause the negative kurtosis value.
MK maps calculated using smoothing processing with various Gaussian kernel of radius and number of error voxel and image sharpness of MK maps are shown in Figure 3. At least 4 pixel kernel size is required to reduce number of error voxel to less than 10 %, which, as a consequence, reduces image sharpness by approximately 29 %.
Discussion
The result suggests that the estimation error caused by signal noise depends on DKI parameters of tissue and that Gibbs ringing artifacts causes the negative kurtosis values. In cortico-medullary junction which often suffer from a black voxel of MK map, the Dapp and Kapp of gray matter are known to be relatively small and Gibbs ringing artifacts are generated due to large differences on signal intensity between cerebrospinal fluid and surrounding tissue. The fact agrees with our findings. Gaussian filter with 4 pixel kernel of radius can effectively reduce the negative kurtosis value but also reduce image sharpness by approximately 29 %. This point should always be kept in mind when DKI is applied in clinical diagnosis.Conclusion
We reveal the causes of the estimation error by using simulation and the relationship between reducing the estimation error and image blurring by using spatial smoothing processing. This findings will be useful for clinical diagnosis using DKI.Acknowledgements
No acknowledgement found.References
1. Jensen JH, Helpern JA, Ramani A, et al. Diffusional kurtosis imaging: the quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. 2005;53(6):1432-1440.
2. Wang JJ, Lin WY, Lu CS, et al. Parkinson disease: diagnostic utility of diffusion kurtosis imaging. Radiology. 2011;261(1):210-217.
3. Raab P, Hattingen E, Franz K, et al. Cerebral gliomas: diffusional kurtosis imaging analysis of microstructural differences. Radiology. 2010;254(3):876-881.
4. Veraart J, Van Hecke W, Sijbers J. Constrained maximum likelihood estimation of diffusion kurtosis tensor using a rician noise model. Magn Reson Med. 2011; 66(6):678-686.
5. De K, and Masilamani V. Image Sharpness Measure for Blurred Images in Frequency Domain. Procedia Engineering. 2013;64:149-158.
Figures