1646
Intravoxel Incoherent Motion (IVIM) Fingerprinting1Center for Neuroimaging, Department of Radiology and Imaging Sciences, Indiana University, School of Medicine, Indianapolis, IN, United States, 2Center for Advanced Imaging Innovation and Research (CAI2R), New York University, School of Medicine, New York, NY, United States, 3Siemens Shenzhen Magnetic Resonance Ltd., Shenzhen, China
Synopsis
Intravoxel incoherent motion (IVIM) imaging employs a bi-exponential diffusion model to estimate capillary contributions to the diffusion-weighted signal. Major challenges of IVIM are long acquisition time, long processing time, and image distortion associated with EPI acquisition. In this work, we proposed a novel framework for rapid and distortion-free IVIM imaging called IVIM-Fingerprinting. It employs a single-shot acquisition scheme and an advanced image reconstruction scheme in combination with the recently proposed concept of MR Fingerprinting. Its performance was demonstrated both for simulation and for in-vivo studies.
Introduction
Intravoxel incoherent motion (IVIM) imaging employs a bi-exponential diffusion model to estimate capillary contributions to the diffusion-weighted (DW) signal.1 A rich literature has demonstrated that IVIM can improve characterization of tumors, stroke, and cirrhosis compared to standard DW imaging (DWI).2-5 IVIM imaging involves collection of a series of DW images at different b-values, followed by estimation of relevant parameters, including the diffusion coefficient (D), pseudo-diffusion coefficient (D*), and perfusion fraction (f), by fitting a nonlinear bi-exponential model. As a result, major challenges of IVIM imaging include long acquisition time, long computation time, and image distortion associated with EPI acquisition. In this work, we proposed a novel framework for rapid and distortion-free IVIM imaging called IVIM-Fingerprinting. It employs a single-shot acquisition scheme in combination with advanced sparse image reconstruction6-8 and the recently proposed concept of MR Fingerprinting.9 Its performance was evaluated both for simulation and for in-vivo studies.Methods
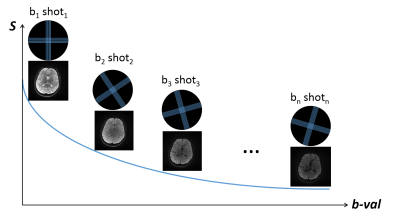
K-space trajectory: Golden-angle Multi-BLADE acquisition with parallel imaging acceleration. A multi-BLADE turbo spin echo sequence was used, where multiple blades can be acquired within one shot.10 The sequence handled non-CPMG problem with phase insensitive preparation. However, instead of acquiring a full k-space with multiple shots, similar to our previous work,11-12 we reduced to single shot with two perpendicular blades and rotated the blades along the b-value with golden angle (111.25°) (Figure 1).13 Parallel imaging (GRAPPA) was used with mutual calibration,14 in which each blade serves as the calibration data for its perpendicular pair.
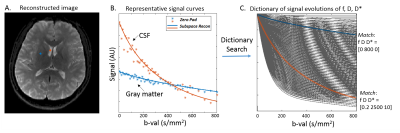
Fingerprinting image reconstruction: Subspace and locally low-rank constrain (subspace-LLR). The sparsity of the IVIM images was exploited in two ways: first, the temporal signal curves were transformed to a low-dimensional subspace using representation basis learned from a dictionary of signal evolution generated with physically plausible values of f, D* and D following equation 1; Second, a LLR regularization was used to further enforce local sparsity in the subspace domain as previously described.8 The reconstruction produced a series of DWIs, from which IVIM parameters were generated on a pixel-by-pixel basis by searching the maximally correlated entity in the dictionary as in the magnetic resonance fingerprinting (MRF) method,9 as shown in Figure 2.
Si=S0 [fe-bD*+(1-f)e-bD] equation 1
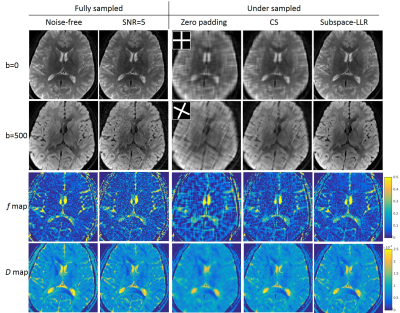
Simulation with human brain data: We simulated realistic DWIs data using a digital phantom with known f, D and D*. Realistic coil sensitivity maps were used, and noise was added to each channel at an aggressive noise level of SNR=5. We retrospectively undersampled k-b (b-value) space with a two-BLADE trajectory as in Figure 1. For comparison, data was reconstructed using both subspace-LLR and compressed sensing with PCA constraint (CS) that does not compensate for signal decay.
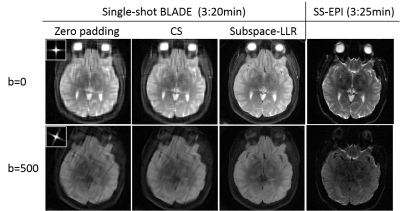
In vivo acquisition: The single-shot multi-BLADE sequence was performed on a healthy volunteer on a 3.0T Siemens Prisma scanner with a 20-channel head and neck coil. Fifty b-values ranging from 0 to 800 s/mm2 were sampled, resulting a total of 50 shots. Each shot covered an undersampled k-space with two perpendicular blades with a blade size of 22×192 (echo train length=11 and GRAPPA R=2). Other parameters included 1.2×1.2mm2 in-plane resolution, TE=44ms, TR=4000ms, 24 slices with 4mm thickness, total acquisition time=3:20. For comparison, single-shot EPI was acquired at the same resolution with an acquisition time of 3:25.
Results
Simulation results at SNR=5 were shown in Figure 3. The golden-angle two-BLADE trajectory produced incoherence aliasing in zero padded DWIs. CS removed some of the aliasing, but was not sufficient. On the other hand, subspace-LLR restored sharp contrast for both b-values, yielding similar quality to that of the fully sampled images. The “denoise” effect can be appreciated from the comparable image quality to the noise-free DWIs at higher b-value.
The in vivo experiments (Figure 4) demonstrated consistent results to the simulations (Figure 3). Subspace-LLR outperformed CS in removing aliasing and restoring image quality/resolution and diffusion contrast. SS-EPI with similar acquisition time showed severe geometric distortions, which were not seen in the single-shot multi-BLADE acquisition.
Discussions
Inheriting from its predecessor, PROPELLER imaging, the multi-BLADE sequence has the advantages of self-navigation, robustness to patient motion, and minimal distortion. By reducing to single shot and combining with golden angle, it produces incoherent aliasing that is suitable for sparse image reconstruction. The results demonstrated that subspace-LLR method was effective at removing aliasing and restoring DWI contrast. In addition, the dictionary search step, inspired by the MRF concept, was computationally efficient bypassing nonlinear model fitting. Future evaluation of the proposed framework in a patient cohort would be necessary to validate its performance and robustness.Acknowledgements
The authors thank Peng Cao (University of California, San Francisco) and Tao Zhang (GE healthcare) for their inspiring discussions. This work was supported by Grants NIH R01AG053993.References
1. Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988 Aug;168(2):497-505.
2. Federau C, Maeder P, O'Brien K, Browaeys P, Meuli R, Hagmann P.Quantitative measurement of brain perfusion with intravoxel incoherent motion MR imaging. Radiology. 2012 Dec;265(3):874-81.
3. Koh DM, Collins DJ, Orton MR. Intravoxel incoherent motion in body diffusion-weighted MRI: reality and challenges. AJR Am J Roentgenol. 2011 Jun;196(6):1351-61.
4. Sigmund EE, Cho GY, Kim S, Finn M, Moccaldi M, Jensen JH, Sodickson DK, Goldberg JD, Formenti S, Moy L. Intravoxel incoherent motion imaging of tumor microenvironment in locally advanced breast cancer. Magn Reson Med. 2011 May;65(5):1437-47.
5. Yáo T. Li, Jean-Pierre Cercueil, Jing Yuan, Weitian Chen, Romaric Loffroy, Yì Xiáng J. Liver intravoxel incoherent motion (IVIM) magnetic resonance imaging: a comprehensive review of published data on normal values and applications for fibrosis and tumor evaluation. Quant Imaging Med Surg. 2017 Feb; 7(1): 59–78.
6. Feng L, Otazo R, Jung H, Jensen JH, Ye JC, Sodickson DK, Kim D. Accelerated cardiac T2 mapping using breath-hold multiecho fast spin-echo pulse sequence with k-t FOCUSS. Magn Reson Med. 2011 Jun;65(6):1661-9.
7. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn Reson Med. 2015 Feb;73(2):655-61.
8. Tamir J, Uecker M, Chen W, Lai P, Alley MT, Vasanawala SS, Lustig M. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn Reson Med. 2017 Jan;77(1):180-195.
9. Dan Ma, Vikas Gulani, Nicole Seiberlich, Kecheng Liu, Jeffrey L. Sunshine, Jeffrey L. Duerk, and Mark A. Griswold. Magnetic Resonance Fingerprinting. Nature. 2013 Mar 14; 495(7440): 187–192.
10. Alsop DC. Phase insensitive preparation of single-shot rare: application to diffusion imaging in humans. Magn Reson Med 1997; 38: 527–533.
11. Wen Q, Kodiweera C, Dale BM, Shivraman G, Wu YC. Rotating single-shot acquisition (RoSA) with composite reconstruction for fast high-resolution diffusion imaging. Magn Reson Med. 2017 Mar 20.
12. Wen Q, Graham M, Drobnjak I, Zhang H, WU YC. Improving angular resolution in multi-shot turbo spin-echo diffusion imaging using rotating single-shot acquisition (RoSA). Proceedings of the 25th Annual Meeting ISMRM, Honolulu, 2017; 0179.
13. Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the Golden Ratio for time-resolved MRI. IEEE Trans Med Imaging. 2007 Jan;26(1):68-76.
14. Li Z, Pipe JG, Aboussouan E, Karis JP, Huo D. A parallel imaging technique using mutual calibration for split-blade diffusion-weighted PROPELLER. Magn Reson Med. 2011 Mar;65(3):638-44.
Figures