Synopsis

Prostate diffusion EPI scans suffer from geometric distortions, signal pile-up and signal drop-out due to differences in susceptibility values at interface between prostate and rectal-air. In this work, an integrated model based framework is proposed that can correct for signal pile-up in regions of severe distortions and can compensate for any translational offsets that may exist between different scans. In-vivo validation of the proposed method is done in patients.

Introduction

Prostate diffusion EPI scans suffer from geometric distortions, signal pile-up and signal drop-out due to differences in susceptibility values at interface between prostate and rectal-air. Techniques have been proposed that can correct for geometric distortions using an additional B0 map that measures frequency offset from resonance at different spatial locations. In regions of severe signal pile-up, these techniques are prone to failure in recovering the underlying true signal. Furthermore, due to drifts and inaccuracies in the measurement of the center frequency [1], the reconstructed images for the EPI scans can be shifted in the phase encoding direction. These shifts are not present for the B0 scan that has a higher bandwidth, thus making use of a B0 map difficult. In this work, using a set of EPI data acquired in blip-up and blip-down phase encoding directions, an integrated model based framework is proposed that can correct for signal pile-up in regions of severe distortions and compensate for any translational offsets between different scans. Validation of proposed method is done in two patients.

Method

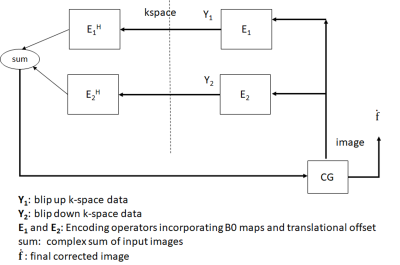
In presence of translational offset along the phase encoding direction, the distorted k-space Y can be related to ideal image f via following model [2]:

$$\mathbf{Y}(k,l)=\sum_{n=0}^{N-1}\sum_{m=0}^{M-1} \mathbf{f}(m,n)e^{-i2\pi(\frac{mk}{M}+\frac{(n-Δn_0)l}{N})}e^{-i2\pi(\triangle \mathbf{B_0} (m,n)t(k,l))} $$

$$\mathbf{Y}=\mathbf{Ef}\space\space\space Eq(1)$$

where E is the encoding operator that contains translational offset and off-resonance related effects, m, n are image indices and k, l are k-space indices, t(k,l) is the sample time for location (k,l) in k-space, ΔB₀ is the B₀ map, Δn₀ is the translational offset whose direction varies with direction of phase encoding (+ve for blip up and –ve for blip down scans).

The proposed method has following two steps:

1) Estimating the translational offset: The translational offset Δn₀ is estimated as the parameter that maximizes the mutual information (MI) similarity measure between preliminary model based reconstructions for blip-up and blip-down EPI data by solving the following unconstrained problem:

$$ \widehat{Δn_0}=arg_{Δn_0}max(MI(\mathbf{E_{1}}^{H}\mathbf{Y_{1}}, \mathbf{E_{2}}^{H}\mathbf{Y_{2}}))\space\space\space Eq(2)$$

where E₁ and E₂ are encoding operators for blip-up and blip-down data that differ in times of the k-space samples, Y₁ and Y₂ are the acquired blip-up and blip-down k-space data for b-value of 0 .

2) Model based Reconstruction: For each b-value, the EPI data acquired in blip-up and blip-down scans can be combined into a single formulation by setting Y=[Y₁ Y₂]^T and E=[E₁ E₂]^T in Eq (1). Model based reconstruction is done (Fig. 1) from combined k-space data Y in a manner analogous to iterative SENSE reconstruction [3] that solves Hermitian-symmetric form of Eq (1) based on conjugate gradient method [4] .

Experiments

Results and Discussion

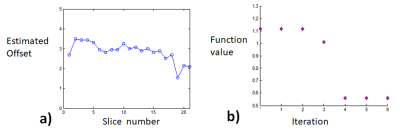
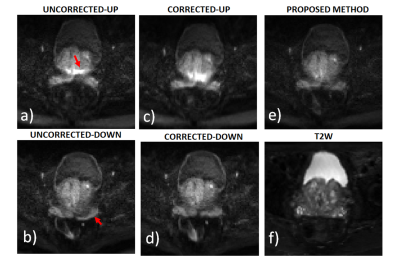
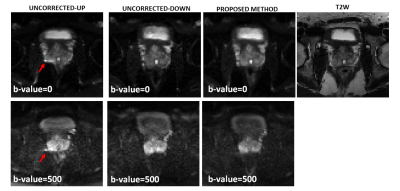
For patient 1, the values of optimal translational offset (in pixels) as a function of slice number is shown in Fig.2a together with convergence plot as function of iteration number in Fig. 2b. The median optimal translational offset was in the range of 3-4 pixels across all the slices. In Fig. 3 and 4, the model based reconstructions from both blip-up and blip-down data are shown for b-values of 0 and 1000 s/mm², respectively. Results for patient 2 are summarized in Fig. 5. In the region around the prostate rectal-air interface, the variation in B₀ was around 120 Hz that corresponds to shift of 7-8 pixels at bandwidth/pixel of ~15.80 Hz in phase encoding direction. This resulted in pile-up in regions where B₀ gradient magnitude was high and its direction was opposite to that of phase encoding gradient (see regions pointed out by red arrows in Fig. 4 and Fig.5). The proposed method corrected for translational offset as well as pile-up artefacts that cannot be corrected using only one-directional phase encoding. In future works, we will investigate the effects due to phase changes that may occur between diffusion weighted blip-up and blip-down EPI scans.

Acknowledgements

References

[1] Andersson et al, NeuroImag 2003

[2] Munger et al, TMI 2000

[3] Stoer et al, Num Math, 1990

[4] Pruessman et al, MRM 2001