1636
High-resolution off-resonance maps improve conformity between distortion-corrected EPI acquisitions and distortion-free references1Center for Image Sciences, UMC Utrecht, Utrecht, Netherlands, 2Department of Biomedical Engineering, Eindhoven University of Technology, Eindhoven, Netherlands
Synopsis
The majority of diffusion acquisitions is affected by geometrical distortions due to susceptibility induced off-resonance effects in the EPI readout. This hampers the use and effectiveness of these images in multiparametric cancer protocols, especially in lipid-rich environments such as the human breast where tissue interfaces cause large but local discontinuities. Preliminary results show that improvements upon existing correction techniques can be made by using high-resolution off-resonance information in distortion correction algorithms.
Purpose
The vast majority of diffusion MRI protocols are conducted using echo planar imaging (EPI) acceleration. Images acquired using this acceleration technique are prone to distortion artifacts, mainly due to off-resonance effects (ΔB0), which hamper easy integration of spatial diffusion metrics in multiparametric analyses of cancer imaging, high-resolution acquisition of diffusion weighted imaging data and ultimately cancer diagnosis. While global field distortions are well incorporated in recent acquisition and processing methods, local distortions are hardly accounted for. In lipid-rich organs, such as the human breast, these off-resonance effects are worsened by highly discontinuous static-field inhomogeneities at tissue interfaces, due to the susceptibility difference between aqueous and adipose tissue environments. The significance of these local effects was demonstrated in previous work reproduced in Figure 1.1 Therefore, we believe including local off-resonance information will improve EPI distortion techniques. In this work, we test the hypothesis that by using off-resonance maps of sufficiently high resolution to capture ΔB0 discontinuities at tissue interfaces for EPI distortion correction, the conformity between the corrected image and a distortion-free reference will improve.Methods
In order to exclude effects caused by subject motion, MR experiments were performed on a motionless pork chop. All experiments were performed using a unilateral breast coil setup on a 7T whole-body MR system (Achieva; Philips, Cleveland, Ohio, USA). The protocol involved two fat-suppressed spin-echo EPI acquisitions with opposed phase encoding directions (2x2x3 mm3, bandwidth/voxel 20 Hz), a non-accelerated spin-echo acquisition with otherwise equal imaging parameters as reference, and two dual-echo ΔB0 measurements at different resolutions (2x2x3 mm3 and 0.7x0.7x3 mm3). In order to avoid lipid bias in the off-resonance measurements, the echo times at which the ΔB0 map was measured were chosen such that a lipid model consisting of the 10 largest resonances was in phase with the water signal.2
Distortion correction was performed using an inverse problem approach resembling techniques described earlier.3, 4 The forward model was described using fast steady state simulations (FORECAST method), restricted to distortions in the phase encoding direction (EPI direction).5 This formulation allows efficient evaluation of $$$A(\Delta B_{0})\cdot x$$$ (the forward model) and $$$A(\Delta B_{0})^{H}\cdot x$$$ (the conjugate transpose of the forward model), where A is the transformation matrix that maps undistorted to distorted space and with the ΔB0 map and corrected image at equal or higher resolution than the measured EPI image. (Direct computation of A was avoided since it is very large and sparse.) The inverse problem was then formulated as a damped least squares problem: $$$Im=\begin{matrix} argmin\\x \end{matrix}\left \| \begin{bmatrix} A\\ \lambda I \end{bmatrix} x - \begin{bmatrix} b\\ 0 \end{bmatrix} \right \|_{2}$$$, where Im is the corrected image, b is the measured EPI data, I is the identity matrix, and the regularization parameter λ was empirically set to 10. This problem was solved using the LSQR algorithm.6
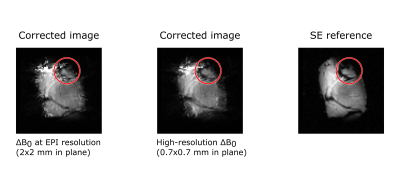
EPI distortion correction was applied to the same pair of oppositely encoded images using the measured ΔB0 map at the EPI resolution (2x2x3 mm3) and at a considerably higher in-plane resolution (0.7x0.7x3 mm3) that better captures local ΔB0 discontinuities at tissue interfaces. The resulting images were compared visually.
Results
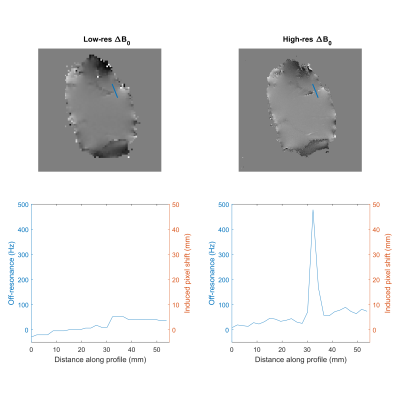
Figure 2 shows the two acquired ΔB0 maps and a profile through the same coordinates side-by-side. Due to the lower sampling in the low-resolution ΔB0 map, discontinuities at tissue interfaces are underestimated. Figure 3 shows the results of the distortion correction both with the high and low resolution ΔB0 map, alongside the undistorted reference. An area is highlighted where the distortion correction markedly benefits from the high-resolution off-resonance information.Discussion
This work demonstrates that EPI distortion correction techniques benefit from high-resolution off-resonance information, especially when many interfaces with adipose tissue are present. Acquiring a high-resolution off-resonance map may be time-consuming and could be undesirable in a clinical protocol. However, several techniques exist that allow the derivation of a high-resolution ΔB0 map from clinically relevant image sources, such as Dixon techniques in DCE MRI, which are standard in multiparametric cancer protocols.Conclusion
A high-resolution off-resonance map allows integration of local ΔB0 discontinuities at tissue interfaces to better describe image distortion at those interfaces. Consequently, using off-resonance maps of a resolution higher than the measured EPI scans improves the conformity between images corrected for EPI distortions and a distortion-free reference.Acknowledgements
This work is part of the IMDI research program with project number 104003019, which is (partly) financed by the Netherlands Organization for Scientific Research (NWO).References
1. van Rijssel M J, Zijlstra F, Seevinck P R, et al. Susceptibility-induced local ΔB0 variations are essential for predicting EPI distortions in the breast. Proc. Intl. Soc. Mag. Reson. Med. 2017; 1389.
2. Boer V O, Luttje M P, Luijten P R, et al. Requirements for static and dynamic higher order B0 shimming of the human breast at 7 T. NMR Biomed. 2014;27(6):625-631.
3. Andersson J L R, Skare S, and Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage. 2003;20(2):870-888.
4. Munger P, Crelier G R, Peters T M, et al. An inverse problem approach to the correction of distortion in EPI images. IEEE Trans Med Imaging. 2000;19(7):681-689.
5. Zijlstra F, Bouwman J G, Braskute I, et al. Fast Fourier-based simulation of off-resonance artifacts in steady-state gradient echo MRI applied to metal object localization. Magn Reson Med. 2017;78(5):2035-2041.
6. Paige C C, and Saunders M A. LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares. Acm Transactions on Mathematical Software. 1982;8(1):43-71.
Figures