Synopsis

This work presents an algorithm that calculates a distortion field to correct a geometrically distorted image using an anatomically precise reference image. The algorithm employs mutual information based rigid image registration with a pyramidal architecture. Validation was performed on simulated distortion fields and in vivo comparison to a measured B₀-fieldmap.

Introduction

Image distortion is a major limitation in multi-contrast MRI exams, in particular, if the treatment is defined on the union of all image information. Most diffusion weighted MRI (DWI) acquisitions are highly sensitive to B₀-field variations leading to severe geometrical distortions. These can be reduced with readout-segmented EPI schemes^1,2, but they are still present in regions where magnetic field shimming is difficult to perform due to the body geometry.

In this work an algorithm is presented to correct geometrical distortions in MRI images. The algorithm does not require an additional B0-fieldmap, and it can be used in multi-contrast MRI studies to retrospectively align images using image information alone.

Materials and Methods

In EPI, geometric distortions $$$\Delta Px$$$ are linked to B₀-field inhomogeneities $$$\Delta B_0$$$ and the pixel-bandwidth $$$BW_{Px}$$$ in phase encoding direction:

$$\Delta Px=\gamma\Delta B_0/BW_{Px}$$.

Without B₀-fieldmap information, distortion correction information can be taken from any sequence with a bandwidth on the order of $$$\gamma\Delta B_0$$$, as it will not be affected by geometrical distortions. In this work, anatomically precise information from a T₂-TSE sequence is used to locally undistort DWI data.

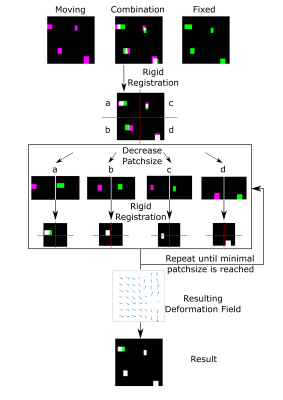
For distortion correction, an algorithm similar to the Lucas-Kanade method in a pyramidal layout³ in optical flow was designed (Figure 1): A DWI and an anatomically precise T₂ image are registered using the mutual information metric⁴. After initial registration the image is divided into a number of overlapping subimages (patches), each with half the side length of the original one. Each of those image patches is subsequently registered to its counterpart, and the result is divided again into subpatches. On each pyramid level, local rigid registration information is passed down to the next for patch selection. The number of pyramid levels N_L can be adjusted by choosing the smallest desired patch size.

The algorithm was tested both on simulated and on in vivo data. The simulated data consisted of a T₂-weighted image of the prostate (normalized to zero mean and unary standard deviation) which was deformed by 100 randomly generated distortion fields. The distorted images were corrected using the original image as a reference. Validation was performed calculating the Euclidean image distance between original and corrected images. Additionally, a volunteer was imaged at a 3T (Siemens Tim Trio) using T₂-weighted and DWI contrasts together with a B₀-fieldmap. T₂ and DWI data were interpolated to a 260x260x96 matrix with 1mm isotropic resolution and registered on 5 Pyramid levels. The resulting distortion field with matrix size 31³ was used to correct the diffusion data and the results were compared to the measured fieldmap.

Results

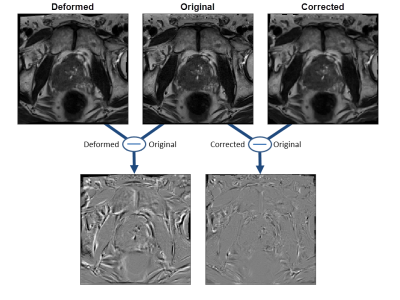
Figure 2 shows an example of the ground truth (original), a randomly deformed and the corrected image together with their respective difference images. Use of the image-based correction algorithm reduced the Euclidean image distance significantly from 0.69 ± 0.06 to 0.21 ± 0.03.

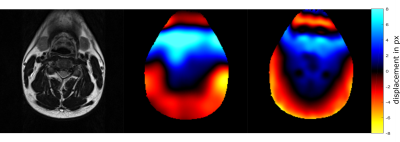
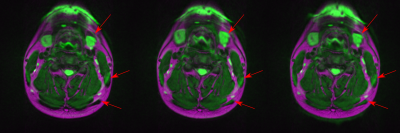
The volunteer experiment shows that the algorithm reproduces the general structure of a measured fieldmap with only minor deviations in the fine structures (Figure 3). In regions of strong distortions, e.g. on the boundaries of the trachea, distortions are so severe that registration fails. Figure 4 shows the results of subsequent correction using fieldmap and registration based correction. Both methods realign anatomical areas well with the corresponding T₂ image, while the case without correction shows severe misalignment.

Discussion

The correction algorithm severely reduces image distortion using mutual information as a metric. This approach is capable of registering different contrasts, such as T₂ and DWI image data. Overlapping anatomical information needs to be present in both reference and distorted images, so that DWI of lowest b-value should be used for correction, as it contains the highest amount of anatomical information.

A major advantage of the proposed method over others⁵ is the incorporation of local information in all spatial dimensions while preserving detection of smallest features.

The algorithm was developed both for 2D and 3D data and can robustly detect deformations in all spatial dimensions. The option to exclude certain dimensions has also been included to account for prior knowledge about the image acquisition (e.g., in DWI the high bandwidth in read direction does not require image correction in this dimension).

Conclusion

Acknowledgements

References

1. Yeom KW, Holdsworth SJ, Van AT, Iv M, Skare S, Lober RM, Bammer R. Comparison of readout-segmented echo-planar imaging (EPI) and single-shot EPI in clinical application of diffusion-weighted imaging of the pediatric brain. AJR Am. J. Roentgenol. 2013;200:W437-443. doi: 10.2214/AJR.12.9854.

2. Porter DA, Heidemann RM. High resolution diffusion-weighted imaging using readout-segmented echo-planar imaging, parallel imaging and a two-dimensional navigator-based reacquisition. Magn. Reson. Med. 2009;62:468–475. doi: 10.1002/mrm.22024.

3. Bouguet J. Pyramidal implementation of the Lucas Kanade feature tracker. Intel Corp. Microprocess. Res. Labs 2000.

4. Viola P, Iii WMW. Alignment by Maximization of Mutual Information. Int. J. Comput. Vis. 1997;24:137–154. doi: 10.1023/A:1007958904918.

5. Chambers MC, Bhushan C, Haldar JP, Leahy RM, Shattuck DW. Correcting inhomogeneity-induced distortion in FMRI using non-rigid registration. In: 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI). ; 2015. pp. 1364–1367. doi: 10.1109/ISBI.2015.7164129.