Synopsis

In diffusion weighted imaging (DWI), multiple acquisitions are acquired and averaged to attain a reasonable SNR level, especially for high spatial resolution or high b-value imaging. However, bulk or involuntary physiological motion during diffusion-sensitizing gradients alters the k-space, creating unpredictable global and/or local phases across multiple acquisitions. Therefore, direct complex averaging of these multiple acquisitions is prohibited. Here, we propose a reconstruction scheme based on modified anisotropic diffusion filtering, which starts with complex-valued acquisitions and corrects the phase issues while improving the SNR. The proposed reconstruction is demonstrated with in vivo DWI of the cervical spinal cord at 1.5T.

Introduction

Methods

Standard ADF: ADF is a popular denoising technique that smooths homogeneous regions while preserving edges, using the following formulation ^2,3:$$I(x ̅,t+Δt)≃I(x ̅,t)+Δt.\frac{∂}{∂t}I(x ̅,t)\qquad(1)$$Here, $$$I(x ̅,t)$$$ is the image intensity at pixel location $$$x ̅$$$ at iteration $$$t$$$, and $$$Δt$$$ denotes the integration step. $$$\frac{∂}{∂t}I(x ̅,t)$$$ is updated iteratively as follows:$$\frac{∂}{∂t}I(x ̅,t)=div(c(x ̅,t).∇I(x ̅,t))\qquad(2)$$An edge detector function is typically chosen as$$c(x ̅,t)=\frac{1}{1+\left(\frac{|∇I(x ̅,t)|}{\kappa}\right)^{2}}\qquad(3)$$where $$$\kappa$$$ adjusts the noise tolerance. Larger values of $$$\kappa$$$ cause more effective denoising, at the expense of reduced edge preservation.

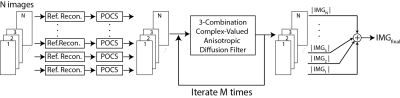
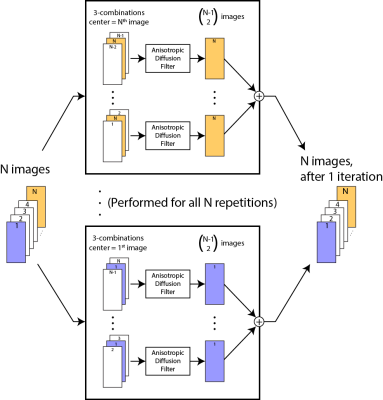
Proposed Reconstruction: As outlined in Fig. 1, each of the N acquisitions is first phase corrected by a refocusing reconstruction using the central 6% of k-space data ⁴. Acquisitions are then individually processed with projection onto convex sets (POCS) partial k-space reconstruction ⁵. Next, multiple acquisitions are processed with a new modified combination ADF (MC-ADF) method (Fig. 2). In contrast to ADF, MC-ADF benefits from structural information shared among acquisitions. To denoise a given acquisition, MC-ADF forms $$$\left(\begin{array}{c}N-1\\2\end{array}\right)$$$ distinct sets of three acquisitions that contain a given acquisition. Each set is stacked to form a 3D volume, and then processed with a complex-valued ADF. The denoised outputs in the middle layer are complex averaged across sets to compute the updated version of the given acquisition. These steps are also completed for all other acquisitions, and the entire procedure is iteratively repeated.

For MC-ADF, a conservative $$$Δt$$$ of $$$\frac{1}{2n}$$$ is chosen to increase the accuracy of the filter, where $$$n$$$ is the number of neighboring pixels (i.e., $$$n=3^3-1=26$$$ for 3D volumes) ⁶. $$$\kappa$$$ is calculated automatically at each iteration, using the 90^th percentile value of $$$|∇I(x ̅,t)|$$$ throughout the image ⁷.$$$\kappa_t=0.5\kappa_0$$$ is used as the stopping criterion, where $$$\kappa_0$$$ is the initial $$$\kappa$$$. Once the stopping criterion is reached, filtered versions of the acquisitions are magnitude averaged.

In vivo DWI experiments: MRI experiments were performed on a 1.5T GE Scanner with an 8-channel cervico-thoracic-lumbar (CTL) coil. In vivo DWI images of the cervical spine were acquired on a healthy subject, in the sagittal plane. A reduced-FOV single-shot echo planar imaging sequence ⁸ was employed with a FOV of 18x4.5 cm², 0.94x0.94 mm² in-plane resolution, 192x48 matrix with 62.5% partial k-space acquisition, TE = 69 ms, 4 mm slice thickness, 16 image acquisitions (NEX), TR = 3.6 s, and b = 500 s/mm² .⁹

Alternative Reconstructions: For all techniques, each acquisition was processed with a refocusing reconstruction followed by the POCS algorithm. Then, the following steps were performed:

1) COMP: Complex averaging of the multiple acquisitions

2) COMP-ADF: COMP followed by standard ADF

3) MAGN: Magnitude averaging of the multiple acquisitions

4) MAGN-ADF: MAGN followed by standard ADF All alternative reconstructions utilized the same number of iterations as the proposed reconstruction.

Results and Discussion

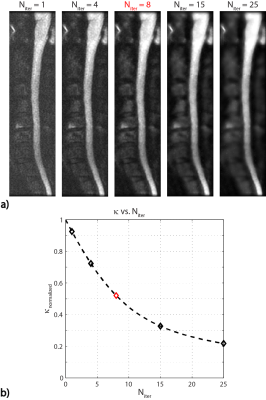
Figure 3a displays the results of proposed reconstruction across iterations. The stopping criterion is reached at the iteration, providing a denoised image with well-preserved edges. Figure 3b depicts the change in with iteration count.

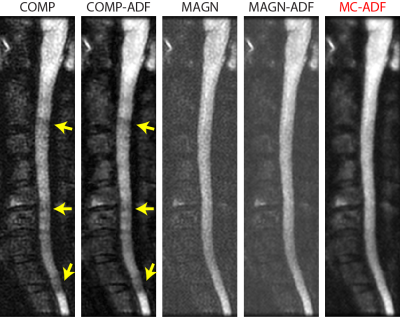
Figure 4 compares all reconstruction techniques. COMP suffers from local phase cancellations along the spinal cord (yellow arrows), which can be confused with increased diffusion. COMP-ADF improves image SNR, but is not able to alleviate phase cancellations. While MAGN is inherently devoid of phase cancellations, it suffers from noise accumulation in the background. MAGN-ADF slightly denoises the image, but noise accumulation persists. In contrast, the proposed reconstruction successfully denoises the image while preserving the edges. Furthermore, the final image is not affected by phase cancellations. Table 1 lists measurements of a no-reference image quality metric for all reconstruction methods ¹⁰. Larger values of this anisotropy metric, $$$\sigma_{anisotropy}$$$ indicate higher image quality. The proposed MC-ADF results in the highest $$$\sigma_{anisotropy}$$$ among all techniques, suggesting superior image quality.

Conclusion

Acknowledgements

References

1. Anderson AW, Gore JC. Analysis and correction of motion artifacts in diffusion weighted imaging. Magnetic Resonance in Medicine. 1994;32:379–387.

2. Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1990;12(7):629–639.

3. Gerig G, Kubler O, Kikinis R, Jolesz F a. Nonlinear anisotrophic filtering of MRI data. IEEE Transactions on Medical Imaging. 1992;11(2):221–232.

4. Miller KL, Pauly JM. Nonlinear phase correction for navigated diffusion imaging. Magnetic Resonance in Medicine. 2003;50(2):343–353.

5. Haacke EM, Lindskogj ED, Lin W. A fast, iterative, partial-fourier technique capable of local phase recovery. Journal of Magnetic Resonance. 1991;92(1):126–145.

6. Weickert J, Romeny B, Viergever M. Efficient and reliable scheme for nonlinear diffusion filtering. IEEE Transactions on Image Processing. 1998;7(3):398–410.

7. Canny J. A computational approach to edge detection. IEEE transactions on pattern analysis and machine intelligence. 1986;8(6):679–698.

8. Saritas EU, Cunningham CH, Lee JH, Han ET, Nishimura DG. DWI of the spinal cord with reduced FOV single-shot EPI. Magnetic Resonance in Medicine. 2008;60(2):468–473.

9. Saritas EU, Lee JH, Nishimura DG. SNR dependence of optimal parameters for apparent diffusion coefficient measurements. Medical Imaging, IEEE Transactions on. 2011;30(2):424–437.

10. Gabarda S, Cristóbal G. Blind image quality assessment through anisotropy. Journal of the Optical Society of America. A, Optics, image science, and vision. 2007;24(12):B42–B51.