1622
Impact of slew rates on the performance of a novel high-gradient breast diffusion probe1Institute of Radiology, University Hospital Erlangen, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 2Center for Medical Physics and Engineering, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 3Department of Diagnostic Radiology, Medical Physics, University Hospital Freiburg, Freiburg, Germany, 4Medical Physics in Radiology, German Cancer Research Center, Heidelberg, Germany
Synopsis
Recent advances in gradient technology, in particular based on the use of local gradient coils, have increased the available gradient strength by almost an order of magnitude. In this context, the question arises what slew rates are required to translate the higher gradient amplitudes into the improved assessment of shorter diffusion times given a certain b-value. This work shows that slew rates are important in high-gradient diffusion experiments (G≥300 mT/m), in particular in low b-value applications (b≤1000 s/mm²).
Introduction
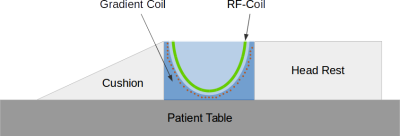
Local gradient coils that have been developed recently are pushing the gradient strength available for diffusion MRI into regimes of almost an order of magnitude higher than in whole-body systems. For example, the Connectome gradient system allows the application of a gradient strength of up to 300 mT/m for head imaging1. We are currently in the design phase for the construction of a “high power diffusion probe” for human breast MRI (Fig. 1). The project is aiming at improving breast diffusion-weighted imaging by locally providing a gradient strength of 1 T/m or greater using non-linear gradient fields. Such strong gradients make shorter diffusion encoding times possible or enable the application of higher b-values. However, the finite rise times of the gradients may impede the benefits of larger gradients. This effect can be mitigated by the use of high slew rates, as is done in the Human Connectome Project, where almost twice the currently available clinical slew rate (200 T/s/m) can be applied on a 7T scanner2. The current work investigates the importance of slew rates in high-gradient diffusion applications (G≥300 mT/m), with a focus on examinations of the apparent diffusion coefficient (i.e. b=1000 s/mm²), and, secondly, with a focus on high b-value applications (b up to 10,000 s/mm²).Methods
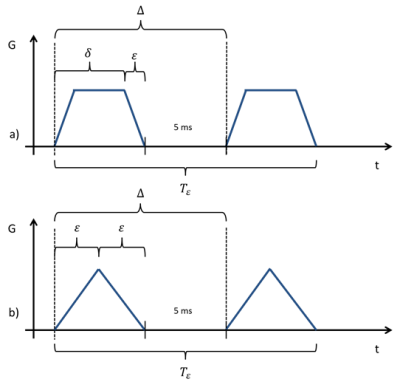
The duration of bipolar diffusion encodings (Fig. 2) is governed by the equations3
$$b_{\text{trapezoidal}}=\gamma^2G^2\left[\delta^2\left(\Delta-\frac{\delta}{3}\right)+\frac{\epsilon^3}{30}-\frac{\delta\epsilon^2}{6}\right]$$
$$b_{\text{triangular}}=\gamma^2G^2\left[\epsilon^2\left(\Delta-\frac{\epsilon}{3}\right)-\frac{2\epsilon^3}{15}\right]$$
where $$$\gamma$$$ is
the gyromagnetic
ratio, $$$G$$$ is the gradient
strength, $$$\delta$$$ denotes the
duration of one gradient pulse, $$$\epsilon$$$ is the rise
time, and $$$\Delta$$$ represents the
time between the leading edges of the gradient pulses.
The total duration of
the diffusion encoding is $$$T_{\epsilon} = \delta +\epsilon + \Delta$$$ (trapezoidal) and $$$T_{\epsilon} = 2\epsilon + \Delta$$$ (triangular).
Results
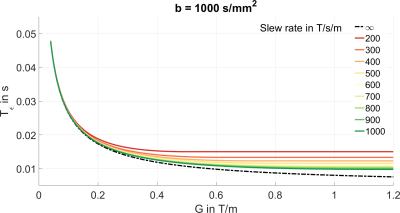
Figure 3 shows $$$T_{\epsilon}$$$ as a function of $$$G$$$. For $$$G<100\,\text{mT/m}$$$, the slew rate of $$$200\,\text{T/s/m}$$$, which is typically available on today’s whole-body scanners, does not cause a relevant prolongation of $$$T_{\epsilon}$$$ in comparison to an infinite slew rate ($$$T_{\epsilon=0}$$$). Thus, the shortest achievable diffusion time is gradient-limited in this regime. For a slew rate of $$$200\,\text{T/s/m}$$$, $$$T_{\epsilon}$$$ becomes shorter when increasing $$$G$$$ up to $$$400\,\text{mT/m}$$$. Beyond this gradient strength, an increase in available $$$G$$$ does not lead to shorter $$$T_{\epsilon}$$$ because the gradients become ‘triangular’ (Fig. 2b). The shortest achievable diffusion time is slew-rate-limited in this regime.
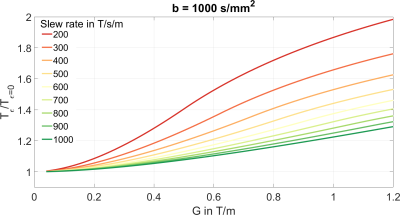
In Figure 4, the relative increase of the minimal achievable diffusion time caused by finite slew rates, i.e. $$$T_{\epsilon}/T_{\epsilon=0}$$$, is plotted as a function of $$$G$$$. At $$$G=300\,\text{mT/m}$$$, there is a slight benefit from increasing the slew rate from $$$200\,\text{T/s/m}$$$ to $$$400\,\text{T/s/m}$$$, as $$$T_{\epsilon}/T_{\epsilon=0}$$$ then decreases from 1.173 to 1.085. Slew rates larger than $$$1000\,\text{T/s/m}$$$ are hardly useful, as $$$T_{\epsilon}/T_{\epsilon=0}$$$ is already as small as 1.034. At $$$G=600\,\text{mT/m}$$$, the benefit from increasing the slew rate from$$$200\,\text{T/s/m}$$$ to $$$400\,\text{T/s/m}$$$ is already much more pronounced, as $$$T_{\epsilon}/T_{\epsilon=0}$$$ then decreases from 1.526 to 1.265. At $$$G=600\,\text{mT/m}$$$, slew rates larger than $$$1000\,\text{T/s/m}$$$ are nevertheless still hardly useful, with a corresponding $$$T_{\epsilon}/T_{\epsilon=0}=1.104$$$. At $$$G=1000\,\text{mT/m}$$$, there is even a benefit of increasing the slew rate beyond $$$1000\,\text{T/s/m}$$$, for which $$$T_{\epsilon}/T_{\epsilon=0}=1.225$$$.
As long as the gradient pulse is not triangular, increasing $$$G$$$ can compensate the prolongation of $$$T_{\epsilon}/T_{\epsilon=0}$$$ that arises from limited slew rates. Figure 5 shows the larger gradient $$$G_{\epsilon}$$$ that is needed with a limited slew rate relative to $$$G_{\epsilon=0}$$$. For $$$G_{\epsilon}=300\,\text{mT/m}$$$ at $$$b=1000\,\text{s/mm²}$$$, $$$G_{\epsilon}/G_{\epsilon=0}$$$ decreases from 1.34 to 1.16 when increasing the slew rate from $$$200\,\text{T/s/m}$$$ to $$$400\,\text{T/s/m}$$$. Thus, increasing the slew rate and enlarging the maximum gradient are both viable options to increase the performance in this regime. The slew rate is more important for smaller $$$b$$$-values and larger $$$G$$$.
Discussion
For$$$\;$$$typical$$$\;$$$human$$$\;$$$whole-body$$$\;$$$scanners$$$\;$$$($$$G<100\,\text{mT/m}$$$, $$$\text{slew rate} = 200\,\text{T/m/s}$$$),$$$\;$$$increasing the available slew rate is of little benefit because the diffusion encoding performance is limited by gradient amplitude. This, however, changes at larger gradient strengths, in particular for low $$$b$$$-values ($$$b<1000\,\text{s/mm²}$$$). One advantage of local gradient coils in comparison to whole-body gradient coils is that the absolute change in gradient field is smaller owing to the reduced spatial extent of the field. This permits the application of higher slew rates because the risk of nerve stimulation is reduced due to smaller magnetic field changes. For the envisaged breast gradient coil, the close location of the gradient coil to the heart still makes a thorough safety assessment mandatory given the need for high slew rates.Conclusion
This work shows that slew rates are important in high-gradient diffusion experiments. For the regime in which the envisaged breast gradient coil is planned to operate, much higher slew rates than those offered by typical clinical systems ($$$200\,\text{T/m/s}$$$) will be necessary to entirely translate the high available gradient strength into relevant clinical applications.Acknowledgements
Financial support by the German Research Foundation (DFG, project number 326944748, LA 2804/7-1, and LA 2804/6-1) is gratefully acknowledged.References
1Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Uğurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
2https://www.humanconnectome.org/study/hcp-young-adult/project-protocol/mr-hardware. Accessed November 6, 2017.
3Price, William S., and Philip W. Kuchel. Effect of nonrectangular field gradient pulses in the Stejskal and Tanner (diffusion) pulse sequence. Journal of Magnetic Resonance 1991;94(1):133-139.Figures