Synopsis

Acquisition time is a major limitation in recovering brain white matter microstructure with diffusion magnetic resonance imaging. Finding a sampling scheme that maximizes signal quality and satisfies given time constraints is NP-hard. Therefore, we propose a heuristic method based on genetic algorithm that finds sub-optimal solutions in reasonable time. Our diffusion model is defined in the $$$q\tau$$$-space, so that it captures both spacial and temporal phenomena. The experiments on synthetic data and in-vivo diffusion images of the C57Bl6 wild-type mouse corpus callosum reveal superiority of our approach over random sampling and even distribution in the $$$q\tau$$$-space.

Introduction

Brain white matter (WM) microstructure recovery with diffusion Magnetic Resonance Imaging (dMRI) requires lengthy acquisition which is unattainable in clinical practice. Dense scanning schemes studied by researchers [1-5] typically take few hours of imaging time, whereas human subjects can tolerate a little more than one hour [6, 7]. Nonetheless, recent in vivo studies of the WM microstructure [7-9] call for more fine-grained investigation of both space- and time-dependent diffusion. In this work, we aim at bridging the gap between growing demands on spatio-temporal ($$$q\tau$$$) probing of dMRI signal [10] and acquisition time limitations. To this end, we propose an acquisition design that reduces the number of samples under adjustable quality loss.

Most of the current acquisition schemes assume the fixed $$$\tau$$$ case, focusing on a dense sampling of the q-space instead [3-5]. However, a pronounced time-dependence in dMRI was recently reported by De Santis et al. [9], Burcaw et al. [11], and Novikov et al. [12]. Their results incline towards paying more attention to temporal phenomena in dMRI signal by incorporating multiple τ variants into acquisition schemes.

Methods

The main goal of our study is to find a $$$q\tau$$$-indexed sampling scheme that best preserves the dMRI signal while satisfying given acquisition time limits [10,13]. We formulate the acquisition design task as an optimization problem. Furthermore, we want our approach to be applicable for real data. To this end, we discretize the spatio-temporal search space by performing a state-of-the-art dense pre-acquisition of dMRI signal. The problem thus boils down to selecting an optimal subset of Diffusion Weighted Images (DWIs), which is NP-hard [13]. Taking into account that the time complexity of our problem grows exponentially with the size of domain, such that global optima cannot be found deterministically within few hours or even few days, we apply a stochastic search engine instead. We use Standard Genetic Algorithm (SGA) [14] for this purpose due to its fast convergence rate, ability to avoid local optima, and the fact that it is based on the mathematically profound Markov Chain model [15].

Experiments

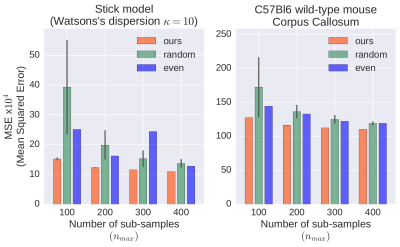
For evaluation of our approach, we used both synthetic diffusion data and in vivo dMRI images of the C57Bl6 wild-type mouse. The dense pre-acquisition of signals covered 40 shells, each of which comprised 20 directions and one $$$b_0$$$-image, i.e. $$$40\times20=800$$$ DWIs plus 40 non-weighted images. We used combinations of 5 separation times $$$\Delta\in\{10.8,13.1,15.4,17.7,20.0\}$$$ [ms] and 8 gradient strengths $$$G\in\{50,100,150,200,250,300,350,400\}$$$ [mT/m]. The gradient duration $$$\delta=5$$$ ms remained constant throughout the experiments. We considered four variants of time limits expressed as budget sizes $$$n_{max}=\{100,200,300,400\}$$$ out of 800 DWIs.

We compared our method with two alternative sampling schemes. One of them, called random, used the uniform random distribution of $$$q\tau$$$ samples in the index space $$$\{1,\ldots,N\}$$$. In the second one, referred to as even, we picked each $$$i$$$-th sample for $$$i=\lfloor kN/n_{max}\rfloor$$$ and $$$k=1,...,n_{max}$$$.

Discussion

As Figure 1 shows, our method outperformed the other two in all analyzed cases, assuring lowest mean squared errors (MSEs) and standard deviations (STDs). We verified statistical significance of the results with the two-sample Student's $$$t$$$-tests with the Bonferroni adjusted significance level $$$\alpha=10^{-5}$$$ and 98 degrees of freedom. In each case, our approach was statistically significantly better than the other schemes.

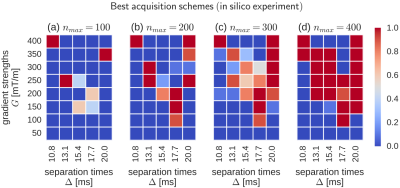
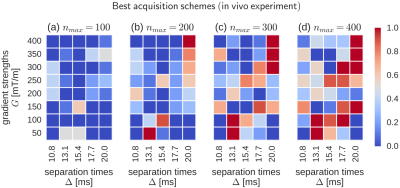
In order to study the stability of our approach, we distilled a single best acquisition scheme found in each of the 50 runs of SGA. Next, we arranged these solutions by MSEs and selected the top 10 out of them. Figures 2 and 3 illustrate the averages of those schemes for in silico and in vivo experiments (respectively). The colors reflect the likelihood of a given $$$(\Delta,G)$$$ pair in the scheme. Note that the concentrations of high likelihood (red squares) tend to form consistent shapes, which suggests that SGA repeatedly converged to the same or highly similar solutions in each run, thus giving stable outputs. In Figure 2, all $$$\Delta$$$ variants appear simultaneously in the schemes, although the largest ones tend to dominate as the $$$n_{max}$$$ increases. At the same time, all but the smallest gradient strengths G are present, most of which concentrate at the center of the range, i.e. $$$200 \leq G \leq 300$$$ [mT/m]. Similar type of clustering is observed in Figure 3, although the low G values are readily more manifested here.

To sum up, the use of SGA allowed us to find acquisition patterns the guaranteed high dMRI signal reconstruction accuracy under given time constraints. Our approach can be applied in follow-up imaging or serve as a starting point when designing acquisition schemes.

Acknowledgements

This work has received funding from the ANR/NSF award NeuroRef; the European Research Council (ERC) under the Horizon 2020 research and innovation program (ERC Advanced Grant agreement No 694665 : CoBCoM); the MAXIMS grant funded by ICM's The Big Brain Theory Program and ANR-10-IAIHU-06; the programs “Institut des neurosciences translationnelle” ANR-10-IAIHU-06 and “Infrastructure d’avenir en Biologie Santé” ANR-11-INBS-0006.

References

[1] Y. Assaf, T. Blumenfeld-Katzir, Y. Yovel, and P. J. Basser, “Axcaliber: a method for measuring axon diameter distribution from diffusion MRI,” Magnetic Resonance in Medicine, vol. 59, no. 6, pp. 1347–1354, 2008.

[2] D. Barazany, P. J. Basser, and Y. Assaf, “In vivo measurement of axon diameter distribution in the corpus callosum of rat brain,” Brain, vol. 132, no. 5, pp. 1210–1220, 2009.

[3] D. S. Tuch, “Q-ball imaging,” MR in medicine, vol. 52, no. 6, pp. 1358–1372, 2004.

[4] V. J. Wedeen, P. Hagmann, W.-Y. I. Tseng, T. G. Reese, and R. M. Weisskoff, “Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging,” Magnetic Resonance in Medicine, vol. 54, no. 6, pp. 1377–1386, 2005.

[5] Y.-C. Wu, A. S. Field, and A. L. Alexander, “Computation of diffusion function measures in q-space using magnetic resonance hybrid diffusion imaging,” IEEE transactions on medical imaging, vol. 27, no. 6, pp. 858–865, 2008.

[6] D. C. Alexander, “A general framework for experiment design in diffusion MRI and its application in measuring direct tissue-microstructure features,” Magnetic Resonance in Medicine, vol. 60, no. 2, pp. 439–448, 2008.

[7] D. C. Alexander, P. L. Hubbard, M. G. Hall, E. A. Moore, M. Ptito, G. J. Parker, and T. B. Dyrby, “Orientationally invariant indices of axon diameter and density from diffusion MRI,” Neuroimage, vol. 52, no. 4, pp. 1374–1389, 2010.

[8] A. Bar-Shir, L. Avram, E. Özarslan, P. J. Basser, and Y. Cohen, “The effect of the diffusion time and pulse gradient duration ratio on the diffraction pattern and the structural information estimated from q-space diffusion MR: experiments and simulations,” Journal of Magnetic Resonance, vol. 194, no. 2, pp. 230–236, 2008.

[9] S. De Santis, D. K. Jones, and A. Roebroeck, “Including diffusion time dependence in the extra-axonal space improves in vivo estimates of axonal diameter and density in human white matter,” NeuroImage, vol. 130, pp. 91–103, 2016.

[10] R. H. Fick, A. Petiet, M. Santin, A.-C. Philippe, S. Lehericy, R. Deriche, and D. Wassermann, “Non-parametric graphnet-regularized representation of dMRI in space and time," Medical Image Analysis, vol. 43, pp. 37–53, 2018.

[11] L. M. Burcaw, E. Fieremans, and D. S. Novikov, “Mesoscopic structure of neuronal tracts from time-dependent diffusion,” NeuroImage, vol. 114, pp. 18–37, 2015.

[12] D. S. Novikov, J. H. Jensen, J. A. Helpern, and E. Fieremans, “Revealing mesoscopic structural universality with diffusion,” Proceedings of the National Academy of Sciences, vol. 111, no. 14, pp. 5088–5093, 2014.

[13] P. Filipiak, R. Fick, A. Petiet, M. Santin, A.-C. Philippe, S. Lehericy, R. Deriche, and D. Wassermann, “Spatio-Temporal dMRI Acquisition Design: Reducing the Number of $$$q\tau$$$ Samples Through a Relaxed Probabilistic Model,” In MICCAI 2017 Workshop on Computational Diffusion MRI (CDMRI 2017), 2017.

[14] J. H. Holland, “Adaptation in natural and artificial systems. an introductory analysis with application to biology, control, and artificial intelligence,” Ann Arbor, MI: University of Michigan Press, 1975.

[15] T. E. Davis and J. C. Principe, “A Markov Chain framework for the Simple Genetic Algorithm,” Evolutionary computation, vol. 1, no. 3, pp. 269–288, 1993.