1615
Optimal Diffusion-weighting Gradient Waveform Design (ODGD): Formulation and Experimental Validation1Laboratorio de Procesado de Imagen, Universidad de Valladolid, Valladolid, Spain, 2Radiology, University of Wisconsin-Madison, Madison, WI, United States, 3Medical Physics, University of Wisconsin-Madison, Madison, WI, United States
Synopsis
Diffusion-Weighted MRI often suffers from signal attenuation due to long TE, sensitivity to physiological motion, and dephasing due to concomitant gradients (CGs). These challenges complicate image interpretation and may introduce bias in quantitative diffusion measurements. Motion moment-nulled diffusion-weighting gradients have been proposed to compensate motion, however, they frequently result in high TE and suffer from CG effects. In this work, the Optimal Diffusion-weighting Gradient waveform Design method that overcomes limitations of state-of-the-art waveforms is revisited and validated in phantom and in-vivo experiments. These diffusion-weighting gradient waveforms reduce the TE and increase the SNR of state-of-the-art waveforms without and with CG-nulling.
Introduction
Diffusion-Weighted MRI (DW-MRI) provides exquisite sensitivity to tissue microstructure in a variety of applications. However, DW-MRI suffers from multiple challenges, including: 1) low signal intensity due to long echo times (TE), 2) motion-related artifacts (eg: signal voids) in tissues affected by bulk motion during the application of DW gradients1-3 (eg: heart and liver), and 3) signal dephasing due to concomitant gradients (CGs)4,5. To overcome these challenges, there is a need for optimized diffusion-weighting waveforms that include high-order motion compensation6 and CG-nulling.
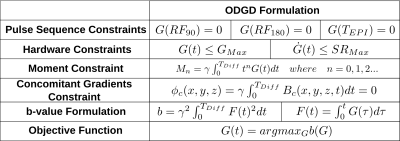
A constrained optimization formulation, termed Convex Optimized Diffusion Encoding6 (CODE), for design of motion-compensated DW gradients has been proposed. Despite the elegant formulation, CODE may not achieve optimal waveforms (maximum b-value for a given TE) due to the approximation of the b-value optimization formulation as a linear optimization problem. This lack of optimality would result in SNR losses. Furthermore, CODE waveforms require additional manipulation to reduce CG effects. Other DW gradient waveforms with motion compensation have been proposed (eg: MONO6, BIPOLAR7, and MOCO8). These waveforms achieve CG-nulling, however, they do not maximize the b-value for a given TE. In order to overcome these limitations, a novel constrained quadratic optimization algorithm termed Optimal Diffusion-weighting Gradient waveform Design (ODGD) was recently presented9. ODGD directly maximizes the b-value subject to nth-order moment-nulling, CG-nulling, and hardware and pulse sequence timing constraints (see Table 1). Despite the promising theoretical properties of ODGD, experimental implementation and validation have not yet been reported.
Therefore, the purpose of this work is to compare feasible waveforms produced by ODGD with state-of-the-art methods, and implement and validate ODGD in phantom and in-vivo experiments.
Methods
In order to minimize TE for a given desired b-value, the ODGD optimization (Table 1) is run iteratively for various TEs (similarly to Ref6).
In this work, nth-order moment-nulled ODGD waveforms without and with CG-nulling (ODGD Mn and ODGD Mn CG, where n=0,1,2, respectively) were designed for b-values=100-2000s/mm2, and TEPI (the EPI readout time required to reach the center of k-space) of TEPI=16.4-46.4ms. Similarly, waveforms with these same parameters were designed using MONO, BIPOLAR, MOCO, and CODE with nth-order moment-nulling.
With IRB approval and informed written consent, liver DWI was acquired in healthy volunteers (N=10) with MONO and 2nd-order moment-nulling waveforms in order to assess motion robustness, signal intensity, and compare SNR across waveform designs. The DW-MRI acquisition was performed at a 3T unit (GE Healthcare, Waukesha, WI) using a spin echo DW-EPI sequence with the following parameters: axial orientation, slice thickness=6mm, FOV=36x36cm, in-plane resolution=2.8x2.8mm, full k-space, and b-values(averages)=[100(4),500(10)]s/mm2. SNR maps were computed as in Ref10.
A water phantom was scanned to assess CG effects with a spin echo DW-EPI sequence using several DW waveforms without and with CG-nulling and multiple diffusion directions, slice thickness=5mm, FOV=26x26cm, in-plane resolution=2x2mm, full k-space, b-values(averages)=[100(1),400(1),600(2),800(4),1000(6)]s/mm2. ADC maps were computed using the maximum likelihood estimator11.
Results
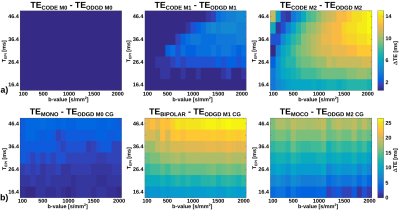
Figure 1 shows the TE difference for a set of b-values and TEPI between ODGD waveforms and MONO, BIPOLAR, MOCO, and CODE waveforms. There is no TE improvement of ODGD M0 over CODE M0, but there is an improvement ranging between 0-3.57% for M1, and 0.63-10.14% for M2. Improvements of ODGD Mn CG over MONO are between 0-4.02% (M0=0), 7.53-16.74% over BIPOLAR (M1=0), and 0.77-12.54% over MOCO (M2=0).
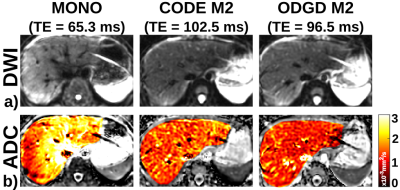
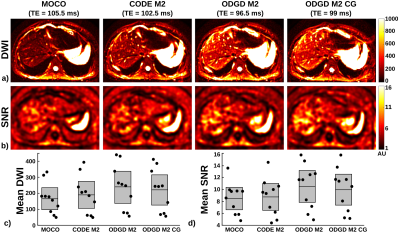
Representative in-vivo liver imaging examples are shown in Figures 2 and 3. CODE M2 and ODGD M2 achieve similar motion robustness (see Figure 2). Figure 3 shows visually apparent signal intensity and SNR increases across all volunteers (measured liver T2=24.38+/-11.4ms) for both ODGD M2 and ODGD M2 CG compared to MOCO and CODE M2. Mean SNR analysis shows significantly higher SNR (p<10-6) of ODGD without and with CG-nulling over MOCO and CODE M2.
Figure 4 shows the biased ADC maps of ODGD M1 due to the additional dephasing introduced by CGs, which in turn lead to spatially-dependent overestimation of ADC. In contrast, BIPOLAR and ODGD M1 CG produce unbiased ADC maps, due to the nulling of CG effects.
Discussion
We have implemented and validated the ODGD formulation presented in Ref9. ODGD allows the design of diffusion-weighting waveforms to reduce bulk motion artifacts and null CGs effects, while minimizing the TE as shown in phantom and in-vivo experiments. ODGD waveforms have potential applications to improve image quality and quantitative measures in neuroimaging and body DW-MRI.
This work has several limitations. Further validation in volunteers and in patients is still required. Extension of the formulation to minimize other artifacts including eddy currents12 is also desirable.
Conclusion
ODGD provides optimized motion-compensated and CG-nulled diffusion gradient waveforms, increasing the SNR compared to state-of-the-art methods.Acknowledgements
The authors acknowledge grants TEC2013-44194-P and VA069U16 from Ministerio de Economía y Competitividad of Spain, and Junta de Castilla y León, respectively. In addition, the authors acknowledge the Consejería de Educación of Junta de Castilla y León and the Fondo Social Europeo. The authors also thank the National Institute of Health, NIDDK Wisconsin Multidisciplinary K12 Urologic Research Center Development Program K12DK100022. Finally, the authors would like to acknowledge research support from GE Healthcare.References
[1] Taouli B, et al. Diffusion-weighted MR Imaging of the Liver1. Radiology. 2009;254(1):47-66
[2] Norris DG. Implications of bulk motion for diffusion-weighted imaging experiments: Effects, mechanisms, and solutions. J Magn Reson Imaging. 2001;13:486-495.
[3] Murphy P, et al. Error Model for reduction of cardiac and respiratory motion effects in quantiative liver DW-MRI. Magn Reson Med. 2013;70(50):1460-1469.
[4] Baron C, et al. The effect of concomitant gradient fields on diffusion tensor imaging. Magn Reson Med. 2012;68:1190-1201.
[5] Bernstein MA, et al. Concomitant Gradient Terms in Phase Contrast MR: Analysis and Correction. Magn Reson Med. 1998;39(2):300-308.
[6] Aliotta E, et al. Convex Optimized Diffusion Encoding (CODE) Gradient Waveforms for Minimum Echo Time and Bulk Motion-Compensated Diffusion Weighted MRI. Magn Reson Med. 2017;77:717-729.
[7] Simonetti OP, et al. Significance of the Point of Expansion in the Interpretation of Gradient Moments and Motion Sensitivity. J Magn Reson Imaging. 1991;1(5):569-577.
[8] Stoeck CT, et al. Secon-Order Motion-Compensated Spin Echo Diffusion Tensor Imaging of the Human Heart. Magn Reson Med. 2016;75:1669-1676.
[9] Peña-Nogales, Ó, et al. Optimal Design of Motion-Compensated Diffusion Gradient Waveforms. Proceedings of 25th ISMRM 2017;3340.
[10] Aja-Fernández, et al. Spatially Variant Noise Estimation in MRI: A Homomorphic Approach. Medical Image Analysis 2015; 20:184-197.
[11] Sijbers J, et al. Maximum-Likelihood Estimation of Rician Distribution Parameters. IEEE Trans Med Imaging. 1998; 17(3):257-361.
[12] Aliotta E, et al. Eddy Current-Nulled Convex Optimized Diffusion Encoding (EN-CODE) for Distortion-Free Diffusion Tensor Imaging With Short Echo Times. Magn Reson Med. 2017; Early view.
Figures