1614

Motion Compensated, Optimized Diffusion Encoding (MODE) Gradient Waveforms
Waqas Majeed1, Prateek Kalra1, and Arunark Kolipaka1

1Radiology, The Ohio State University Wexner Medical Center, Columbus, OH, United States

Synopsis

We present a framework to obtain motion compensated diffusion encoding waveforms that are shorter than all diffusion encoding waveforms available to date. These waveforms can be obtained analytically. We successfully demonstrate the use of these waveforms for cardiac DWI.

Introduction

Diffusion Weighted Imaging (DWI) is based on the principle that MRI images can be sensitized to random self-diffusion by playing diffusion encoding gradients (DEGs). For a given diffusion sensitivity, or b-value, It is important to utilize the shortest DEG waveforms to avoid unnecessary T2 losses. Additionally, it is desirable to design DEG waveforms that are insensitive to bulk motion to enable DWI of organs that are susceptible to physiological motion. To address this issue, Aliotta et al. 1 presented a method named CODE (Convex Optimized Diffusion Encoding) to obtain optimized DEG waveforms with nulled first and second moments (M1 and M2). CODE framework has two limitations: First, CODE waveforms are obtained by optimizing a function that is not equal to the actual b-value. Secondly, CODE waveforms require numerical optimization, and cannot be computed "on the fly" on the scanning computer.

We propose a novel framework to design Motion Compensated, Optimized Diffusion Encoding (MODE) gradient waveforms. We demonstrate that MODE waveforms result in a higher b-value for a given DEG duration, compared with CODE waveforms. Secondly, we provide analytical expressions that can be used to generate MODE waveforms on the fly. Finally, we demonstrate that the diffusion coefficient values obtained using MODE waveforms are consistent with the literature.

Theory

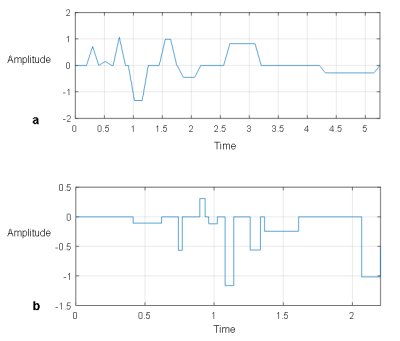
We first introduce Trap8 model waveforms, consisting of 8 non-overlapping trapezoidal pulses with identical ramp times (Figure 1a). Trap8 waveforms are characterized by 25 parameters (8 start times, 8 stop times and ramp time). Another useful waveform model is Sq8, which consists of 8 non-overlapping square pulses and is characterized by 24 parameters (Figure 1b). We obtained analytical expressions of b-value, M1 and M2 for Trp8 as well as Sq8 waveforms.

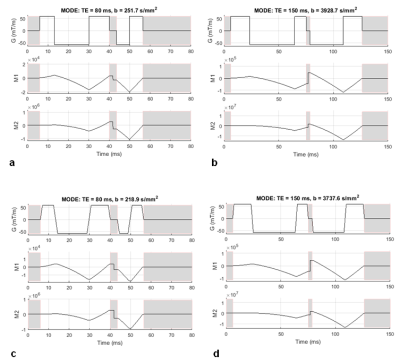
MODE framework consists of three steps: First, optimal waveform configuration of Sq8 waveforms is found. This is achieved by distributing the 8 pulses evenly between the available time-slots and using a constrained optimization algorithm to find waveform configurations with highest b-value for a given waveform duration, under timing and system constraints. Sq8 model is desirable for this step, because waveforms with fewer than 8 pulses can be obtained by combining 8 square pulses. In the second step, it is verified that the optimal configuration for Sq8 waveform is the optimal configuration for Trap8 waveforms as well, by obtaining optimal waveforms with different number of trapezoidal pulses in different available slots, under the timing and system constraints. Figure 2 shows that the optimal configuration remains unchanged for a vast range of b-values. In the third step, general mathematical expressions are derived for the optimal Trap8 configurations. These expressions can be used to design the MODE waveforms on the fly. Figure 3 shows the expressions obtained for the optimal configurations.

Methods

Simulations were performed to compare the duration of M2 compensated MODE and CODE waveforms for a given b-value.MODE waveforms were incorporated into a commercial DWI sequence using the expressions shown in Figure 3. Correction for concomitant fields was incorporated 2. Three healthy volunteers were imaged using the implemented sequence on a 3T MRI scanner with maximum gradient strength of 40 mT/m (Magnetom Skyra; Siemens Medical Solutions, Erlangen, Germany). Scout images were acquired to plan short-axis diffusion weighted scans. The DWI scans were acquired using the following parameters: TR = 2 RRs, TE = 68-70 ms, one 10 mm thick slice, 2.7 mm x 2.7 mm in-plane resolution, in-plane acceleration of 2, 6/8 partial Fourier, bandwidth = 2298 Hz/Voxel, 6 directions with b = 350, one image with b = 100, trigger delay = ~200ms (during ejection). Tensors were reconstructed on voxel by voxel basis, and the trace ADC maps were constructed.

Results

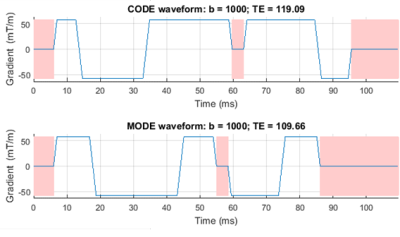
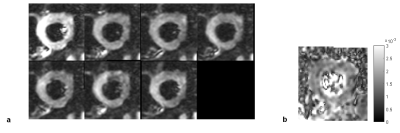
Figure 4 shows CODE and MODE waveforms obtained for b = 1000 for example imaging parameters. Clearly, shorter TE can be obtained using MODE, as compared with CODE. Figure 5a shows diffusion weighted images obtained during ejection from one subject. An ADC map (one average) is shown in Figure 2b. Consistent with the existing literature1, average myocardial ADC values from the 3 subjects were found to be between 0.0015 and 0.0016 mm2/s.

Discussion and Conclusions

We have presented a novel framework for the design of optimal motion compensated diffusion encoding waveforms. These waveforms outperform CODE in terms of shorter TE, and can be computed on the fly using analytical formulas. This framework can also be utilized to obtain optimized preparation waveforms for other applications, such as MR elastography and flow imaging. Future work will focus on comparison of the results obtained with MODE waveforms with those obtained using CODE waveforms.

Acknowledgements

No acknowledgement found.

References

  1. Aliotta, E., Wu, H. H. and Ennis, D. B. (2017), Convex optimized diffusion encoding (CODE) gradient waveforms for minimum echo time and bulk motion–compensated diffusion-weighted MRI. Magn. Reson. Med., 77: 717–729. doi:10.1002/mrm.26166
  2. Meier C, Zwanger M, Feiweier T, Porter D. Concomitant field terms for asymmetric gradient coils: consequences for diffusion, flow, and echo-planar imaging. Magn Reson Med 2008;60(1):128–134.

Figures

Figure 1: Examples of Trap8 and Sq8 waveforms (a and b respectively).

Figure 2: Optimal configurations of Sq8 waveforms for two different TEs are shown in a) and b) respectively. The shaded areas represent excitation pulse + correction scans, refocusing pulse and readout respectively. The optimal configurations were obtained by allowing 4 pulses in each of the gaps. The same configurations were found to be optimal for Trap8 waveforms as well (c and d)

Figure 3: a) The optimal configuration can be described by only 2 parameters, i.e. start times of 2nd and 3rd pulses - Start time of remaining pulses are either fixed, or can be determined in terms of S2 and S3. b) Conventions. c) Expressions of the unknown parameters of the optimal waveform configuration are obtained in terms of the timing of the available time slots. The two unknown parameters are easily found by equating M1 and M2 to 0. 4) b-value expression for the optimal configuration.

Figure 4: MODE waveform results in a lower TE for a given b-value, compared with the CODE waveform. Please note that CODE waveform does not have the optimal configuration.

Figure 5:a) b = 50 (top left) and b=350 images acquired from a volunteer. 6 diffusion directions were used. b) ADC map obtained using the acquired images.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
1614