1605

Diffusion gradient performance optimization for B-tensor encoded q-space trajectory imaging of the human brain
Jan Martin1, Andreas Wetscherek2, Lars Müller3,4, Tristan Anselm Kuder3, Michael Uder1, Bernhard Hensel5, and Frederik Bernd Laun1

1Institute of Radiology, University Hospital Erlangen, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 2Joint Department of Physics, The Institute of Cancer Research and The Royal Marsden NHS Foundation Trust, London, United Kingdom, 3Department Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany, 4CUBRIC, School of Psychology, University of Cardiff, Cardiff, United Kingdom, 5Center for Medical Physics and Engineering, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany

Synopsis

q-Space trajectory imaging is a recently introduced approach for determining microscopic diffusion tensor properties like μFA and orientation coherence. To create the necessary higher order B-tensors special gradient trajectories are needed. The initial implementation of q-space trajectory imaging was based on magic-angle-spinning of the q-vector, and required echo times of 160 ms for b-values of 2000 s/mm2. In the current abstract, numerically optimized gradient trajectories were implemented, which reduced the required echo time to 115 ms. The resulting parameter maps benefited from the increase in signal-to-noise ratio.

Introduction

Diffusion tensor imaging allows for estimating parameter maps closely tied to tissue microstructure, but is unable to resolve subvoxel inhomogeneity of diffusion properties1. This leads to cases of isotropic diffusion being indistinguishable from multiple crossing anisotropic compartments2.

q-Space trajectory imaging (QTI) assumes a distribution of microscopic diffusion tensors within a voxel, instead of a single averaged tensor. This way, additional information about the diffusion on a subvoxel scale may be gained. The signal equation is approximated using a cumulant expansion3: $$S\approx\exp(-<\textbf{B},\langle\textbf{D}\rangle>+\frac{1}{2}<\textbf{B}^{\otimes2},\textbf{C}>) \hspace{40mm} \textrm{(1)}$$ $$$\langle\textbf{D}\rangle$$$ represents the diffusion tensor averaged over a voxel, $$$\textbf{B}$$$ a three-dimensional measurement tensor, and $$$\textbf{C}$$$ the four-dimensional covariance matrix.

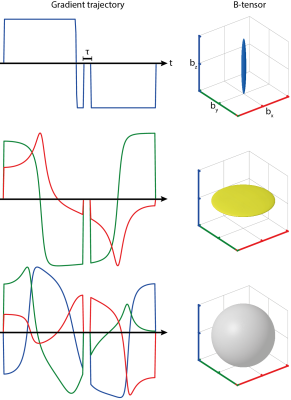
In the initial approach, the required diffusion gradient trajectories were calculated by magic-angle-spinning of the q-vector (qMAS)3,4. The resulting gradients are arranged symmetrically around a 180° spin-echo pulse. An alternative constrained optimization approach allows for asymmetrical gradient waveforms, utilizing the available time better (see Fig. 1)5.

This abstract aims to improve the quality of QTI maps by applying diffusion gradients optimized with constrained optimization.

Methods

Diffusion gradient trajectories were optimized using a constrained optimization scheme5. The b-value was maximized with respect to B-tensor shape, available gradient amplitude (43 mT/m), slew rate (90 T/m/s), and the sequence timing. Gradients were normalized to the Euclidian L2 norm to allow rotations in arbitrary directions. The optimization was carried out for 208 timesteps, yielding B-tensors correct up to order 10-5 for all employed shapes.

Measurements at two different echo times (115 ms and 160 ms respectively) were carried out using a spin-echo sequence with echo-planar readout6. A healthy volunteer (age 23) was scanned in a 3T Magnetom Skyra (Siemens Healthineers, Erlangen, Germany) with a 64-channel head coil. Measurement protocols were approved by the local institutional review board and written consent was obtained prior to scanning. Sequence parameters were as follows: repetition time 4000 ms, 8 slices, resolution 2x2x2 mm3, field-of-view 256x256 mm2, bandwidth 1502 Hz/Px. 11 b-values were evenly spaced up to 2000 s/mm2. Five different B-tensor shapes (linear, planar, spherical, prolate, oblate) were employed in six collinear directions determined by the vertices of an icosahedron7.

Resulting images were motion corrected and smoothed with a three-dimensional Gaussian filter (standard deviation 0.5 voxels)8. Maps of mean diffusivity (MD), fractional anisotropy (FA), microscopic FA (µFA), and normalized orientation coherence (CC) were obtained by fitting the data to Eq. 13.

Gradient trajectory optimization and post-processing was carried out in Matlab9.


Results

The constrained optimization allowed b-values up to 2000 s/mm2 at a minimum echo time of 115 ms. Exemplary gradient trajectories for linear, planar, and spherical B-tensor encoding are shown in Fig. 1.

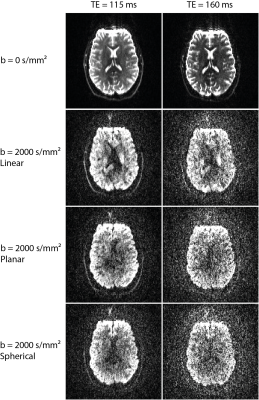
Diffusion-weighted images (DWIs) for a single slice, measured with linear, planar, and spherical B-tensors, are displayed in Fig. 2. At b = 0 s/mm2 brain structures are well resolved for both echo times. However, the overall signal loss at TE = 160 ms is accompanied by an increase in Gibbs ringing artifacts. At b = 2000 s/mm2 and TE = 115 ms structural information is still retained well. In images of the same diffusion weighting, but acquired with TE = 160 ms, the signal falls below the noise level in parts of the brain.

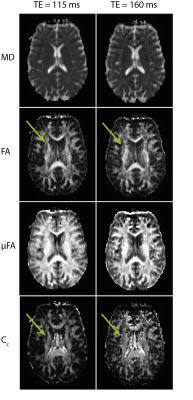
Fitted maps of MD, FA, µFA, and CC for both measurements are shown in Fig. 3. In general, maps fitted to data acquired at TE = 160 ms are more noisy than maps fitted to images measured at the minimum TE = 115 ms. Singular dark pixels in FA, µFA, and CC maps became more common, and finer brain structures are no longer resolved well (e.g. arrows in Fig. 3).


Discussion

QTI with B-tensor encoding is a promising new approach in diffusion MRI. It allows for determining dispersion metrics of distributions of microscopic diffusion tensors within a voxel, but the reliability of QTI parameter maps depends on the signal intensity at high b-values.

We have shown that asymmetrical gradient trajectories optimized with a constrained optimization scheme shorten the required echo time to 115 ms for b-values up to 2000 s/mm2, thus improving the quality of diffusion-weighted data and derived parameter maps. Especially the µFA and CC, which are important for interpreting the underlying diffusion tensor distribution correctly, benefit from the optimization. Besides numerical gradient optimization, the quality of QTI maps may be further improved by higher field strengths and better gradient hardware10.

Conclusion

Using numerically optimized diffusion gradient trajectories is recommendable for measuring data with QTI if one aims at a reliable estimation of tensor parameters like µFA and CC, which are important for determining diffusion information on a subvoxel scale2.

Acknowledgements

Financial support by the DFG (grant number LA 2804/6-1) is gratefully acknowledged.

References

1. Jones D K, Leemans A, Diffusion Tensor Imaging. Methods Mol. Biol., 2011;711:127-144

2. Lasič S, et al. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Frontiers in Physics, 2014;2(11):1-14

3. Westin C-F, et al. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage, 2016;135:345-362

4. Topgaard D, Isotropic diffusion weighting in PGSE NMR: Numerical optimization of the q-MAS PGSE sequence. Microporous and Mesoporous Materials, 2013;178:60-63

5. Sjolund J, et al. Constrained optimization of gradient waveforms for generalized diffusion encoding. Journal of Magnetic Resonance, 2015;261:157-168

6. Stehling M K, et al. Echo-Planar Imaging: Magnetic Resonance Imaging in a Fraction of a Second. Science, 1991;254(5028):43-50

7. Hasan K M, et al. Comparison of Gradient Encoding Schemes for Diffusion Tensor MRI. Journal of Magnetic Resonance Imaging, 2001;13:769-780

8. Nilsson M, et al. Extrapolation-Based References Improve Motion and Eddy-Current Correction of High B-Value DWI Data: Application in Parkinson's Disease Dementia. Plos One, 2015;10(11)

9. MATLAB Release 2015b, The MathWorks, Inc., Natick, Massachusetts, United States

10. McNab J A, et al. The Human Connectome Project and beyond: Initial applications of 300 mT/m gradients. Neuroimage, 2013;80:234-245


Figures

Figure 1: Diffusion gradient trajectories (left) and corresponding B-tensors (right). Red, green, and blue denote the spatial orientations x, y, and z. Shown are the linear (top), planar (middle), and spherical (bottom) case. Gradient trajectories were optimized using a constrained optimization approach5. During a pause interval τ, the 180°-spin-echo-pulse is played out (slice selection gradient not shown). Due to the numerical optimization, the diffusion gradients before and after the 180°-pulse are not required to be symmetrical, thus allowing for a more efficient use of the available time.

Figure 2: Acquired diffusion weighted images. Shown is a single slice measured with different B-tensor shapes. At b = 0 s/mm2 images have an acceptable quality for both, TE = 115 ms (left) and TE = 160 ms (right). However, at TE = 160 ms and b = 2000 s/mm2 the combined effects of long echo time and high diffusion weighting drop the signal level below the noise floor in parts of the brain. Optimized gradients allow the same amount of weighting at shorter TE = 115 ms, improving image quality in return.

Figure 3: Fitted QTI parameter maps. Shown are MD, FA, μFA, and CC for a single slice. Pixel values were computed by fitting the diffusion-weighted images to Eq. 1. When comparing maps fitted to data acquired at TE = 115 ms (left) to TE = 160 ms (right), a decrease in variance and the amount of dark pixels can be observed. The green arrow marks a region where structural information would be lost without optimized gradients, due to the increase in variance.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
1605