Synopsis

The compartmentalized structure of biological tissues demands a representation of individual compartments and a description of diffusion within them. We identified a quadratic potential energy profile, recently studied in-depth by Yolcu et al. (Phys Rev E, 93, 052602, 2016), as the effective energy landscape for restricted diffusion as far as gradient waveforms featuring long pulses are concerned. Our simulations suggest that the stochastic effective force on the center-of-mass position is approximately linear, thus providing further support for the Hookean effective force model.

Introduction

Theory

When the diffusion gradient pulses are long enough for molecules to probe the pore space, the signal can be written as

$$E = \tilde p_\mathrm{cm} (\mathbf q_1,\delta_1) \, \tilde p_\mathrm{cm} (\mathbf q_2,\delta_2) \ldots \, \tilde p_\mathrm{cm} (\mathbf q_N,\delta_N)\ , $$

where $$$\tilde p_\mathrm{cm} (\mathbf q,\delta)$$$ denotes the Fourier transform of the center-of-mass distribution during the application of gradient pulses of duration $$$\delta$$$ yielding the wavevector $$$\mathbf{q}$$$. The center-of-mass distribution approaches a Gaussian in the limit of long duration [4]. Therefore, its Fourier transform and hence the signal, $$$E$$$, approach Gaussians as well.

Another situation in which the signal is Gaussian is one where the $$$q$$$-value and/or the size of the compartment is so small that the compartmental signal attenuation is still well-represented by a Gaussian decay.

While restricted diffusion becomes a difficult problem in higher dimensions except for a few special geometries, diffusion under a Hookean force is much more tractable, and it behooves one to adopt the latter model when its features are all that can be observed. Hence, we consider diffusion under a (dimensionless) parabolic confining potential $$$U(\mathbf x)=(1/2) \mathbf{x}^T \mathbf C \mathbf x$$$, where $$$\mathbf C$$$ is the confinement tensor [3]. For this process, the center-of-mass distribution and the signal are Gaussian for any duration even though the particles are bounded.

Insights from the one-dimensional problem

For illustrating the size-confinement correspondence, we consider diffusion restricted by two parallel plates separated by a distance $$$L$$$. Since a zero-mean Gaussian distribution is determined by its variance matrix, an effective confinement value for restricted diffusion can be obtained by setting the variances of the center-of-mass distributions associated with the two problems equal.

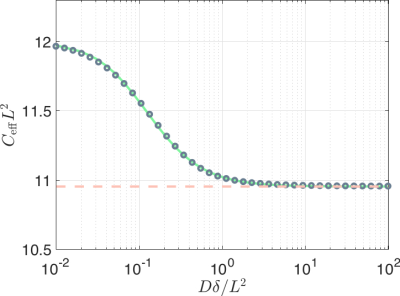
First, we consider the case $$$q L \ll 1$$$. As shown in Figure 1, the effective confinement value (assuming well-separated pulses) varies within a very narrow range. Therefore, employing the asymptotic correspondence instead of the numerical one (green curve in Figure 1) would provide an acceptable estimate of $$$L$$$.

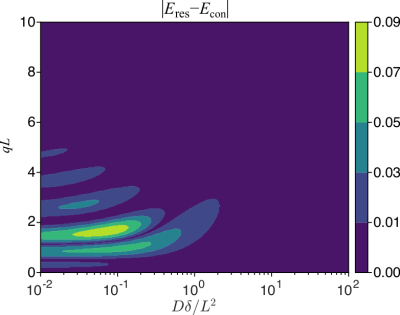
The signal provided by the confinement model can only be an approximation to the true signal for restricted diffusion for other values of $$$q$$$ or $$$\delta$$$. To investigate the discrepancy, we compare the signal for the restricted diffusion problem to that for the Hookean model featuring the long-time asymptotic value of the effective confinement. Fig.2 shows that such discrepancy is below 0.01 for a very large portion of the parameter space that could be probed, e.g., for micron-scale compartments. Such differences are not detectable when the signal-to-noise ratio is 100 or less, justifying the confinement description as a reliable substitute in studies involving restricted diffusion.

Simulations of the boundary force

We define an effective force, $$$F_\mathrm{eff}$$$, based on the impulse the particles experience during a duration $$$\delta$$$, i.e.,

$$ F_\mathrm{eff}\delta = \int_0^\delta F(t) \, \mathrm{d} t \ .$$

The effective force has a perfectly linear dependence on the center-of-mass of each and every trajectory in the Hookean model. On the other hand for restricted diffusion, $$$F_\mathrm{eff}$$$ is proportional to $$$-\Delta N/\delta$$$, where $$$\Delta N$$$ denotes the difference in the number of collisions the particle makes with the respective walls.

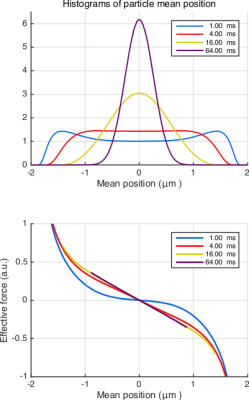
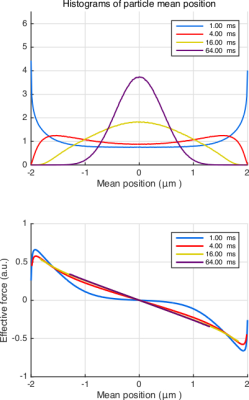
In Fig.3(top), we plot the histograms of center-of-mass position for different durations to illustrate the approach to a Gaussian as the time is prolonged. In Fig.3(bottom), we plot the average of the net effective force against the center-of-mass position. Remarkably, $$$F_\mathrm{eff}$$$ is linearly related to the mean position for an overwhelming portion of the particles even for moderate times. Importantly, the same conclusion can be drawn for more complicated problems, albeit for a different value of the effective confinement. This point is illustrated in Fig.4 for the case of sticky walls.

Discussion and conclusion

Acknowledgements

References

1. Mitra PP, Halperin BI. Effects of finite gradient-pulse widths in pulsed-field-gradient diffusion measurements. J Magn Reson A. 1995;113:94–101.

2. Stejskal EO. Use of spin echoes in a pulsed magnetic-field gradient to study anisotropic, restricted diffusion and flow. J Chem Phys. 1965;43:3597–3603.

3. Yolcu C, Memic M, Simsek K, et al. NMR signal for particles diffusing under potentials: From path integrals and numerical methods to a model of diffusion anisotropy. Phys Rev E. 2016;93:052602.

4. Neuman CH. Spin echo of spins diffusing in a bounded medium. J Chem Phys. 1974;60:4508–4511.

5. Stejskal EO, Tanner JE. Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient. J Chem Phys. 1965;42:288–292.

6. Grebenkov DS. NMR survey of reflected Brownian motion. Rev Mod Phys. 2007;79:1077–1137.