1596
An efficient regularization method for diffusion MAP-MRI estimation1Institute of Medical Device and Imaging, National Taiwan University College of Medicine, Taipei, Taiwan, 2Molecular Imaging Center, National Taiwan University, Taipei, Taiwan, 3Graduate Institute of Brain and Mind Sciences, National Taiwan University College of Medicine, Taipei, Taiwan, 4Department of Medical Imaging, National Taiwan University Hospital, Taipei, Taiwan
Synopsis
In the study, we proposed a regularization method for MAP-MRI estimation, called ReMAP. This method includes a regularization term in the cost functional in order to penalize the coefficients. The penalty is a simple diagonal matrix with entries determined only by the order of the Hermite functions, where higher order functions take more penalization, therefore, this method is easy to implement. In addition, ReMAP outperforms MAP-MRI in both estimation efficiency and accuracy, revealing that the regularization term is crucial for a robust estimation. Therefore, ReMAP is an improved version of MAP-MRI and would be beneficial for clinical studies.
Introduction
Mean Apparent Propagator (MAP)-MRI1 is a robust method to convert the diffusion attenuation signals to the diffusion propagator function through the well-known Fourier transform (FT) relationship. MAP-MRI fits with a linear combination of Hermite functions, so the diffusion-relevant microstructures can be represented by a few coefficients, serving as an efficient dimension reduction method. In addition, various diffusion indexes can be readily calculated from the MAP-MRI coefficients, such as generalized fractional anisotropy (GFA), rendering MAP-MRI a good quantifying method for clinical studies.2 In the present study, we proposed a regularization method for MAP-MRI estimation, called ReMAP. This method can substantially shorten the processing time and greatly improves the estimation stability.Theory
An important property of Hermite functions $$$\phi_n$$$ is that their Fourier counterparts $$$\psi_n$$$ are also Hermite functions but with weighting $$$i^{-n}$$$. MAP-MRI employs this property to formulate the diffusion signal $$$S(q)$$$ and the diffusion propagator $$$P(r)$$$, yielding
$$S(q)=\sum_{N=0}^{N_{max}}\sum_{\{n_1,n_2,n_3\}}^{}c_{n_1,n_2,n_3}\phi_{n_1,n_2,n_3}(A,q)=\sum_{j=1}^{M}c_j\phi_j(A,q)$$
and
$$P(r)=\sum_{N=0}^{N_{max}}\sum_{\{n_1,n_2,n_3\}}^{}c_{n_1,n_2,n_3}\psi_{n_1,n_2,n_3}(A,r)=\sum_{j=1}^{M}c_j\psi_j(A,r),$$
where $$$N_{max}$$$ is the maximum order, $$$n_1+n_2+n_3=N$$$, and $$$A=diag(u_x,u_y,u_z)$$$ represents the scaling matrix. Here $$$\phi_{n_1,n_2,n_3}(A,q)=\phi_{n_x}(u_x,q_x)\phi_{n_y}(u_y,q_y)\phi_{n_z}(u_z,q_z)$$$ , $$$\psi_{n_1,n_2,n_3}(A,r)=\psi_{n_x}(u_x,r_x)\phi_{n_y}(u_y,r_y)\phi_{n_z}(u_z,r_z)$$$, $$$\phi_n(u,q)=\phi_n(2 \pi uq)$$$, and $$$\psi_n(u,r)=\frac{i^n}{\sqrt{2 \pi u}}\phi_n(\frac{r}{u})$$$ are the FT of $$$\phi_n(u,q)$$$. For the sake of simplicity, we also re-index the terms when expressing $$$S$$$ and $$$P$$$.
In the MAP-MRI algorithm, the estimated coefficients are those minimize the data-matching functional $$$E_1={\parallel\bf \phi c-y\parallel}^2$$$, while subject to the positivity constrain $$$\bf \psi c \geq0$$$. Here $$$\bf c$$$ is the coefficient vector, $$$\bf y$$$ the data vector, $$$\bf \phi$$$ the design matrix, and $$$\bf \psi$$$ the constraint matrix. ReMAP modifies MAP-MRI by defining the cost functional as $$$E=E_1+\rho E_2$$$, where $$$E_2$$$ is a Tikhonov regularization and $$$\rho$$$ is a weighting parameter balancing $$$E_1$$$ and $$$E_2$$$. ReMAP defines $$$E_2$$$ as
$$E_2=\langle LS(q\prime),LS(q\prime)\rangle=\sum_{j=1}^M\sum_{k=1}^M\int c_j c_k L\phi_j(q\prime) \cdot \overline{L\phi_k(q\prime)}dq\prime={\bf c^TUc},$$
where $$$q\prime=2\pi Aq$$$ is the scaled coordinates and $$$L$$$ is a differential operator. Now we introduce another property of Hermite functions: they are solutions of the differential equation
$$(-\triangledown^2+q^Tq)\phi_j(q)=\lambda_j\phi_j(q)$$
with eigenvalues $$$\lambda_j=2N_j+3$$$. Physically, the first term and second term on the left hand side represent the kinetic energy and potential energy of the system, respectively. The operator $$$L$$$ is defined to represent the total energy, yielding
$$U_{jk}=\int \lambda_j\phi_j(q\prime) \cdot \overline{\lambda_k\phi_k(q\prime)} dq\prime=\lambda_j^2\delta_j^k.$$
Put all terms together, the optimal solution of ReMAP is$$\widehat{\bf c}=\arg_{\bf c}\min({\bf c^T(\phi^T\phi+\rho U)c-2c^T\phi^Ty}).$$ The quadratic programing procedure with the positivity constrain $$$\bf \psi c\geq0$$$ is employed to estimate the coefficients.
Materials and methods
ReMAP was implemented with Matlab, where the official function, quadprog, was used to estimate the coefficients. We empirically set the maximum order $$$N_{max}$$$ to 6 and the weighting parameter $$$\rho$$$ to 0.006. The diffusion propagators were assumed to be symmetric about the origin, so only terms with $$$N$$$ even have to be considered, leading to a total of 50 coefficients. The ReMAP method was compared to the MAP-MRI method (i.e., $$$\rho=0$$$). Both methods were applied on a representative diffusion data from the WU-Minn Human Connectome Project. The fiber orientations were estimated according to the local maximum of the orientational distribution function (ODF), which can be readily calculated from the estimated coefficients1.Results
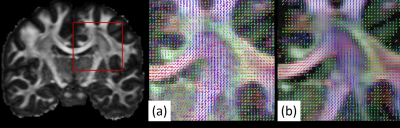
The coefficient estimation time of MAP-MRI and that of ReMAP are 18.53 min and 6.25 min, respectively. Figure 1 displays the orientation maps of (a) MAP-MRI and (b) ReMAP. Clearly, the MAP-MRI method produces a large amount of spurious orientations, such as those in the corpus callosum regions. In contrast, the ReMAP method results in an organized structure and coincides well with the known anatomy.Discussion
In the study, we proposed a regularization method for MAP-MRI estimation, called ReMAP, which slightly modifies the optimization process of the original MAP-MRI algorithm by including a regularization term in the cost functional. The purpose of the regularization is to penalize the estimated coefficients. The coefficient penalty comprises a differential operator which physically represents the total energy of the system. Besides, the penalty integrates over the scaled, rather than the original, q-space. Both lead the coefficient penalty to a simple diagonal matrix with entries determined only by the order of the Hermite functions, where higher order functions would take more penalization. The form of the regularization method is also compatible with the quadratic programing algorithm, therefore it is easy to implement. The computation time of ReMAP is one-third of that of MAP-MRI, indicating that the new method substantially improves the estimation efficiency. According to the orientation maps, the estimation accuracy of ReMAP also outperforms that of MAP-MRI, revealing that the inclusion of the regularization term is crucial for a robust estimation. Therefore, we conclude that ReMAP is an improved version of MAP-MRI and would be beneficial for clinical studies.Acknowledgements
The diffusion data was provided [in part] by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657). This work was supported in part through funding from the Ministry of Science and Technology, Taiwan (MOST 103-2325-B-002-040, NSC101-2321-B-002-079), the National Health Research Institute, Taiwan (NHRI-EX101-10145NI), the Ministry of Economic Affairs, Taiwan (100-EC-17-A-19-S1-175) and the National Institute of Mental Health, USA (1U01MH093765-01).References
1. Ozarslan, E. et al. Mean apparent propagator (MAP) MRI: a novel diffusion imaging method for mapping tissue microstructure. Neuroimage 78, 16-32, doi:10.1016/j.neuroimage.2013.04.016 (2013).
2. Avram, A. V. et al. Clinical feasibility of using mean apparent propagator (MAP) MRI to characterize brain tissue microstructure. Neuroimage 127, 422-434, doi:10.1016/j.neuroimage.2015.11.027 (2016).