1595
Multicompartment modelling of diffusion-weighted MRI data with no prior assumptions1Physical Sciences for Health Doctoral Training Centre, University of Birmingham, Birmingham, United Kingdom, 2Institute of Cancer and Genomic Sciences, University of Birmingham, Birmingham, United Kingdom, 3Department of Oncology, Birmingham Children's Hospital, Birmingham, United Kingdom, 4School of Computer Science, Birmingham, United Kingdom
Synopsis
Multi-compartment modelling of Diffusion-Weighted MRI data can provide additional diffusion related parameters. However, to ensure meaningful parameters are attained, multi-compartment models have to make several assumptions prior to fitting, including initial parameter values and multi-step fitting procedures. The novel Autoregressive Discrete Acquisition Points Transformation (ADAPT) method was applied to in vivo data. ADAPT demonstrated that it could infer the number of compartments within the data. When 1- and 2-compartment ADAPT models were investigated, the ADAPT coefficients were found to correlate with the parameters attained by the Apparent Diffusion Coefficient (ADC) and the Intravoxel Incoherent Motion (IVIM) models.
Introduction
An apparent diffusion coefficient (ADC) image is the simplest way to observe the diffusive behaviour of biological tissue. The ADC provides a single parameter to describe the average diffusivity for each voxel1. The diffusion signal detected will be the combination of many different occurring water-moving processes, such as intracellular and extracellular movement and motion within blood vessels2. If information for each of these compartments can be extracted from the signal, a greater understanding of the fundamental nature and structure of tissue can be attained. The Intravoxel Incoherent Motion (IVIM) model is a bi-exponential model commonly used to explain the phenomena of diffusion and perfusion within tissue and has been shown to have clinical relevance3. However, such a model needs prior knowledge with the requirement of a multistep fitting procedure and estimation of initial parameter values. The complexity and variability presented by multi-exponential models thus results in the prevalence of the ADC model. In the presented study a novel fitting method for modelling the multi b-value diffusion weighted imaging, The ‘Autoregressive Discrete Acquisition Points Transformation’ (ADAPT), method. Such a method treats the diffusion signal as a function of acquisition points(n)4, thus allowing each data point to be modelled as a function of the b-values and previous signal values(lags). As the ADAPT fitting method infers all information from the lagged data points; no prior information or multistep fitting processes are required. The aim of this study was to evaluate a range of different compartment ADAPT models and compare its resulting parameters to those of the ADC and IVIM fitting methods.Method
A volunteer brain scan (age 25), SNR≈50, was acquired on a Philips Achieva 3T TX MRI scanner at Birmingham Children’s Hospital using a 32-multichannel receiver head coil. The diffusion-weighted MRI sequence used a sensitivity-encoded (SENSE) approach with the following parameters: b-values=[0,20,40,80,110,140,170,200,300, 500, 1000], FOV 230x230mm , TR/TE 3,214/84ms, matrix size 256x256, 5mm slice thickness and in plane resolution 0.9x0.9mm . ADC and IVIM fitting methods were applied to the diffusion-weighted image. The IVIM model was fitted using a non-linear least squares minimisation with the Levenberg-Marquardt algorithm, and a constrained 2-parameter fitting method5. The ADAPT method was fitted using matrix minimisation techniques for the equation:
$$$ln(S_n)=\sum_{i=0}^{Q} β_ib_{n-i} + \sum_{j=1}^{P} α_jln(S_{n-j})$$$
The Signal value can be modelled as a linear summation of previous Signal and b-values. Sn-Signal at acquisition point n; bn-b-value at acquisition point n. αj,βi-minimisation coefficients. P,Q-the number of lag terms. A range of ADAPT(P,Q) orders from (0,0) to (3,3) were investigated. The optimum order was selected with the corrected Akaike Information Criterion (AICc)6.
Results
The ADC and IVIM model were fitted to the diffusion-weighted image and the optimum model was selected for each voxel using the AICc. The parametric map in Figure-1c demonstrates that the majority of voxels are best fitted by the IVIM model when compared to the ADC model. A range of ADAPT orders were also considered (Figure-1b). Regions considered to be mono-exponential in the multiexponential analysis correlated to ADAPT(0,0). Most tissue was found to be best represented by ADAPT(1,0), although some higher order behaviour was observed.
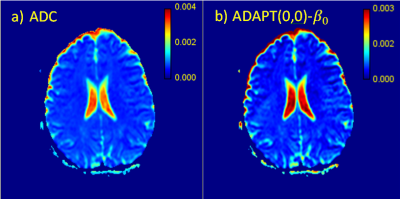
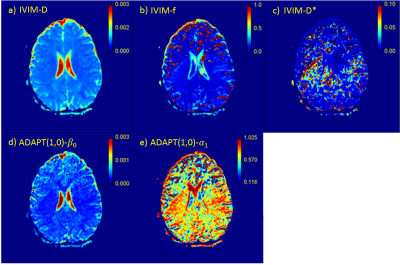
ADAPT(0,0) was applied to a whole brain imaging slice (Figure-2b) and the β0 parametric map was found to correlated strongly with the ADC values (r=0.99) (Figure-4). ADAPT(1,0) was also applied to the same slice , creating β0 and α1 parametric maps (Figure-3). The ADAPT(1,0) parametric maps were compared to the IVIM parametric maps of f, D and D*. A very strong correlation between ADAPT(1,0)-β0 and D was observed (r=0.94) and α1 had a substantial correlation to the IVIM-f map (r=0.72).
Discussion
The optimum ADAPT model appears to infer to the number of components within the data, with some regions containing cerebrospinal fluid (CSF) exhibiting ADAPT(0,0) behaviour. This is to be expected as ADAPT(0,0) is mathematically equivalent to the ADC model. Individual voxels exhibiting higher order behaviour are most likely to be explained by noise. The cluster of ADAPT(3,0) (Figure-1) on the edge of the CSF could potentially be caused by partial volume effects in which compartments from both brain matter and the CSF are detected7. The strong correlation between the ADAPT(1,0) and IVIM-f and IVIM-D parameters indicate that a relationship between ADAPT(1,0) and the IVIM model exists.Conclusion
The novel ADAPT model has be found to model in vivo data, with the number of ADAPT terms correlating to the number of exponential terms observed. The relationship between the ADAPT and IVIM parameters suggest that complex diffusion biomarkers can be obtained by making no prior assumptions about the nature of the data.Acknowledgements
This work was funded by the Engineering and Physical Sciences Research Council (EPSRC) through a studentship from the Sci-Phy-4-Health Centre for Doctoral Training (EP/L016346/1), the National Institute for Health Research (NIHR) via a research professorship (13-0053), the Paediatric Experimental Cancer Medicine Centre and Free Radio in conjunction with Help Harry Help Others (HHHO).References
1. Sener RN, Comput Med Imaging Graph;25 (4): 299-326 (2001)
2. Koh DM et al., AJR; 196(6): 1351-1361 (2011)
3. Pang Y et al, Magn Reson Med 69(2) 553-562 (2013)
4. Stearns SD, Digitial Signal Processing with examples in MATLAB, CRC Press(2003)
5. Meeus EM et al, J Magn Reson Imaging 45(5) 1325-1334 (2017)
6. Cavanaugh JE, Stats Probab Lett, 33(2) 201-208 (1997)
7. Metcalfe-Smith E et al. “A novel method for the detection of the number of compartments in diffusion MRI data”, ISMRM 2018 abstract (ID: 2881)
Figures