1591
The influence of gradient nonlinearity on spherical deconvolution approaches: to correct or not to correct?1Image Sciences Institute, University Medical Center Utrecht, Utrecht, Netherlands, 2Cardiff University Brain Research Imaging Centre, Cardiff, United Kingdom
Synopsis
Gradient non-linearities affects diffusion weighted imaging (DWI) as it can result in geometric distortions and spatially varying b-values and gradient directions. The effect is more severe at high gradient strengths. Spherical deconvolution, in particular, relies on a spherical sampling of q-space, which might be affected due to gradient nonlinearities. In this work, we explored the sensitivity of two widely used spherical deconvolution approaches to the gradient non-linearity effect by investigating FOD peak orientation deviations, and evaluate a modified version of DRL that can take into account spatially varying diffusion gradients and weighting. Monte-Carlo simulations and two datasets from the HCP project were used for evaluation.
Introduction
In MRI gradients are used spatially encode the signal along x, y and z directions. In the case of gradient nonlinearity, gradients deviate from their ideal behavior, giving rise to geometric distortions. In diffusion MRI this can additionally result in a sampling of q-space that spatially differs from the a priori defined sampling[1-3]. These effects scale with gradient amplitude and can be prominent for ultra-strong gradients. The purpose of this study is to evaluate the effect of gradient nonlinearities on spherical deconvolution (SD) approaches, which specifically rely on a spherical sampling of q-space and are used to resolve the fiber orientation distribution functions (FODs). Whereas for constrained spherical deconvolution (CSD)[4] measurements have to explicitly be mapped back onto a sphere using a signal decay model[5], damped Richardson-Lucy (dRL)[6] is a dictionary-based approach that can potentially deal with b-matrix deviations by defining a voxel-specific dictionary. In this study, we compare differences in peak orientations from FODs for DRL with and without correcting the b-matrix for gradient non-linearity effects and CSD without taking the modified b-matrix into account.Methods
The original DRL uses a common set of b-values and gradient directions (g) for all voxels, thus the deconvolution matrix H can be created once and is subsequently used for all voxels. Here, we compute the b-value and g experienced in each voxel as a result of gradient nonlinearities by taking into account the provided gradient deviations. We subsequently generate a voxel-wise deconvolution matrix H that could theoretically correct for the spatially varying b-matrix introduced by the gradient field. To verify this hypothesis, we performed experiments comparing FODs estimated with the original and modified DRL and compared this to CSD.
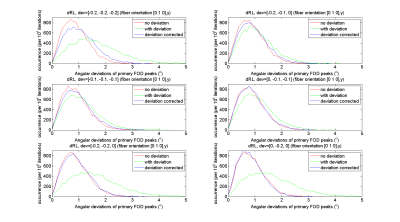
Simulations Simulated signals of b = 3000s/mm2 were generated from a tensor model for a single fiber population along x, y and z direction; and a single fiber along y-direction with corresponding gradient field deviations within [-0.2:0.1:0] range along [x, y, z] directions. Rician noise was added with SNR030 in 104 realizations. In addition, we simulated a deviation from the unit vector of [-0.13, -0.14, -0.05], which was sampled from a real dataset acquired with strong gradients. This gradient deviation is relatively larger in x and y directions compared to the z-direction.
In-vivo data Normal and modified DRL was applied to two datasets from the Human Connectome Project (HCP)[7], which included 18 b=0s/mm2 and 90 directions at b=3000s/mm2. The primary FOD peaks were extracted[8] voxel-wise and the angular deviations between original DRL and modified DRL peaks were calculated. The voxel-wise gradient deviations released with the HCP data were used to create the voxel-wise deconvolution matrix.
Results
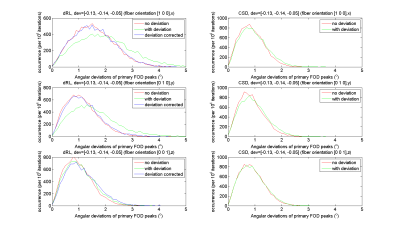
Fig.2 shows the distribution of the FOD peak angular deviations between the original DRL, the modified DRL (left) and CSD (right); with (green-lines) and without (red-lines) the gradient deviation added in the simulated signals. CSD peak orientations did change only slightly, and the angular deviation from the ground truth stays within 2◦. The angular deviations of dRL FOD peaks were the largest for the non-corrected DRL method when non-linearity was simulated. When taking the deviating b-matrix into account in the deconvolution matrix, the angular deviation distributions shift from 0◦-5◦ (green-lines) to 0◦-4◦ (blue-lines). The distribution of angular deviations of modified DRL FOD peaks were matching well with the distribution of FODs estimated from signals without any gradient deviations. From Fig.3, one can appreciate that the angular deviations and FOD peaks are smaller when the gradient deviations were corrected by the modified DRL.
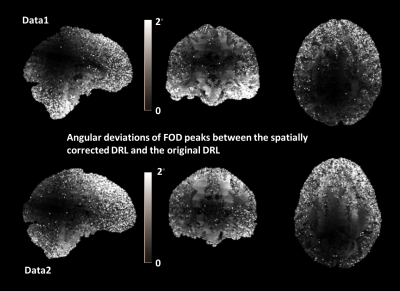
Fig.4 shows the angular deviations of primary DRL FOD peaks of HCP data, with and without taking the spatially varying b-values and gradients into account (i.e. the modified DRL and the original DRL). Similar patterns can be found in both datasets. Towards the center of the gradient field there is rarely any difference between the modified DRL and the original DRL considering the primary FOD peak orientations. To the edges, there is a maximum angular difference of 2◦.
Conclusion & Discussion
In this study we explored the sensitivity of spherical deconvolution approaches, particularly damped Richardson-Lucy (DRL), to the effect of gradient non-linearity. Monte-Carlo simulations and HCP datasets were used in the work. By comparing the FOD peak orientations we found that spatially correcting the b-values and gradient improved the performance of DRL in the simulations, while CSD seems to be more robust to the gradient non-linearity effects at the investigated b-value. In the in-vivo data, angular deviations up to 2◦ can be spotted on the edges of the brain dataset, when the gradients were voxel-wise corrected in the modified DRL. Future work will further characterize this effect as a function of b-value, SNR, and other acquisition parameters.Acknowledgements
The research of F.G. was funded by China Scholarship Council.
CMWT is supported by a Rubicon grant (680-50-1527) from the Netherlands Organisation for Scientific Research (NWO) and Wellcome Trust grant (096646/Z/11/Z).
References
1. Malyarenko, Dariya I., Brian D. Ross, and Thomas L. Chenevert. "Analysis and correction of gradient nonlinearity bias in apparent diffusion coefficient measurements." Magnetic resonance in medicine 71.3 (2014): 1312-1323.
2. Bammer, R., et al. "Analysis and generalized correction of the effect of spatial gradient field distortions in diffusion‐weighted imaging." Magnetic resonance in medicine 50.3 (2003): 560-569.
3. Sotiropoulos, Stamatios N., et al. "Advances in diffusion MRI acquisition and processing in the Human Connectome Project." Neuroimage 80 (2013): 125-143.
4.Tournier, J-Donald, Fernando Calamante, and Alan Connelly. "Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution." Neuroimage 35.4 (2007): 1459-1472.
5. J. Morez, J. Sijbers, and B. Jeurissen, "Spherical Deconvolution of Non-Spherically Sampled Diffusion MRI Data", International Society for Magnetic Resonance in Medicine, 2017.
6. Dell'Acqua, Flavio, et al. "A modified damped Richardson–Lucy algorithm to reduce isotropic background effects in spherical deconvolution." Neuroimage 49.2 (2010): 1446-1458.
7. Van Essen, David C., et al. "The WU-Minn human connectome project: an overview." Neuroimage 80 (2013): 62-79.
8. Jeurissen, Ben, et al. "Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging." Human brain mapping 34.11 (2013): 2747-2766.
Figures